物理实验的设计方法

第五节　物理实验的设计方法

要进行物理实验的设计，必须了解在物理实验中具有普遍意义的思想方法。

周密思考，分解课题，精心设计

英国科学家贝弗里奇指出：“最有成就的实验家常常是这样的人：他们事先对课题加以周密思考，并将课题分成若干关键的问题，然后精心设计为这些问题提供答案的实验。”

下面让我们看看伽利略是怎样设计研究自由落体实验的。伽利略在比萨大学任教时就开始对自由落体进行研究，直到1638年才在《关于力学和局部运动两门新科学的谈话和数学证明》中系统地论述了这一研究成果。

伽利略首先从一个理想实验得出的佯谬入手，对亚里士多德的落体学说（即物体的下落速度与其重量成正比的学说）提出反驳，证明这一学说是错误的。

自由落体运动是否像亚里士多德提出的那样，是匀加速运动呢？伽利略认为应该用实验做出检验，但要直接验证是恒量在当时是很困难的。于是，伽利略运用数学知识，根据他的假设推出了匀加速运动通过的距离与时间的平方成正比的公式，即

这是一个便于直接测定的关系式。

为了“冲淡重力”、减缓下落运动，伽利略进行了著名的斜面实验。实验发现：一个从静止开始下落的物体在相等的时间间隔经过的各段距离之比等于从1开始的一系列奇数之比，即为1∶3∶5∶7…从而证实了落体所经过的各种距离总是同所用时间的平方成正比。

为了把斜面实验的结论推广到竖直情况下的自由落体运动，伽利略提出了等末速度假设，即静止物体不论是沿竖直方向还是沿不同斜面的同一高度下落，到达末端时具有相同的速度，也就是说，物体在下落中所得到的速度只由下落的高度决定，而与斜面的倾斜程度无关。对此，伽利略用了一个单摆实验验证了这个假设。根据这个假设，可得到沿斜面下滑的加速度g₁与自由下落的加速度g之间的关系

由这个关系，不难从g求出g₁伽利略根据这个关系得出了自由落体做匀加速运动的结论。

伽利略把科学的实验方法发展到了一个全新的高度，从此开始了物理学的一个新的时代，使物理学走上了真正科学的道路。

原理正确，实际可行

实验的设计，在原理上必须是正确的，同时又应是实际可行的。

有人曾设计了这样一个测量“凹面镜焦距”的实验：因为凹面镜的焦距近似地等于镜的球面半径的1/2，所以，只要测定了球面的半径，就可以知道凹面镜的焦距。

为测量球面的半径，使一个小滚珠在球面上通过最低点做往复运动。如果运动的幅度很小，则滚珠的运动可以看做简谐振动，其周期与单摆的周期相同，镜的球面半径就相当于单摆的摆长。测出滚珠往复运动的周期，就可求得球面的半径，从而求得凹面镜的焦距。

这个设计，看似有理，但从原理上来说则是错误的，因为滚珠的转动惯量对运动还有影响。例如，当球心到滚珠的半径与竖直线的夹角为θ时，滚珠质心的加速度并不等于gsinθ，因此滚珠做往复运动的周期也和相当摆长的单摆不同。而如果用一个小滑块来代替滚珠，则由于摩擦，滑块实际上是不能做往复运动的。所以，这只能算是一道物理习题，而不能算是实验设计。

明确物理实验的三个基本组成部分

在物理学史上有一些实验设计得非常巧妙，不仅目的明确、思考周密，而且抓住关键、出奇制胜。例如，1911年卢瑟福的α粒子散射实验，就是巧妙设计的典范。该实验的目的是为探明原子内部电子和其他粒子的分布状况，以检验汤姆逊的原子“枣糕”模型。

卢瑟福认为，要实现这一目的，惟一的方法是打碎原子。为了打碎原子，他选择了α粒子作为“炮弹”。他还对实验的过程和结果作出预计，认为当粒子穿过原子时，有的会发生偏转，有的会反射回来。这是他经过周密思考而提出的实验设计的基本思想。

根据这一实验设计思想，卢瑟福又精心设计了巧妙的实验装置：一端放着α粒子源R，用以放射“炮弹”；中间放一张极薄的金箔F，作为α粒子轰击的目标；另一端放置闪烁屏S，用以显示α粒子的轰击效果，以便收集实验数据。

实验结果表明：当α粒子射向金箔时，大多数α粒子顺利穿过原子，少数发生了偏转，极少数被反弹回来，具体地说，仅有1/8000的α粒子偏转大于90°，其中极个别的接近180°。

卢瑟福对实验数据进行了严密的数学计算和理论分析后得出结论：原子内部大部分空间没有大质量的粒子，所以，大多数α粒子能顺利通过；原子内有一个体积极小、质量极大的核，使极少数α粒子被弹回。卢瑟福的实验结果否定了汤姆逊的原子结构模型。卢瑟福于1911年提出了被称为“行星模型”的原子有核结构模型，推进了人们对原子结构的认识。

从这个例子中可以看出，一个完整成功的物理实验大致可分为三个组成部分：

（1）实验源：它是实验信号的发生源，如a粒子散射实验中的a粒子源R。

（2）实验对象：它是实验源信号所作用的对象，如α粒子散射实验中的金箔F。

（3）实验效果显示器：这是用以呈现实验对象接受实验源信号作用后所产生效应的部分，以便通过直接或间接的方式进行效果的观察，如α粒子散射实验中的闪烁屏S。

当然，上述分法不是绝对的。在有些简单的实验中，实验源和实验对象是一个；在有的实验中，实验效果就显示在实验对象身上。

实验应尽可能在“纯化”的条件下进行

用实验方法来研究某一问题时，一般先要对研究对象和物理过程作初步的分析，弄清影响实验过程的外部条件以及内部的各个因素之间关系，抓住主要矛盾，排除各种干扰，使实验尽可能在“纯化”的条件下进行。

对于观察某一现象的物理实验，为了要使研究的现象与其他无关的现象区别开来，必须尽量排除各种干扰因素。例如，为了观察硫酸铜溶液中的铜离子的扩散现象，必须先将清水盛在细、高的容器中，再用长颈漏斗将硫酸铜溶液缓慢地注入容器的底部，然后静置于恒温的环境中，这样才能避免机械的扰动和热对流的影响，使我们观察到的是真正的扩散现象。

这个实验一般要经过一二天的时间，才能看出蓝色的硫酸铜溶液和清水的界面稍有模糊。笔者曾经在一些资料上看到有关扩散现象实验的设计：将容器内的液体加热，观察到扩散现象明显加快，由此说明分子运动的平均速度随温度的升高而增大。只要稍加分析就能看出，这种设计是错误的。

我们知道，分子的平均速度和绝对温度的平方根成正比，即，设实验中液体的温度由300K（27℃）升到350K（77℃），分子的平均速度才增大了原来的0.08倍，由此而造成的扩散速度加快在课堂的几十分钟内是不能观察到的。如果我们观察到了液体混合（我们不说扩散）速度的明显加快，显然是由于热对流的结果。

对于测量物理量的实验，也存在一个测量条件的“纯化”问题。我们大家都熟悉的用半偏法测量电流计内阻的电如下图路。

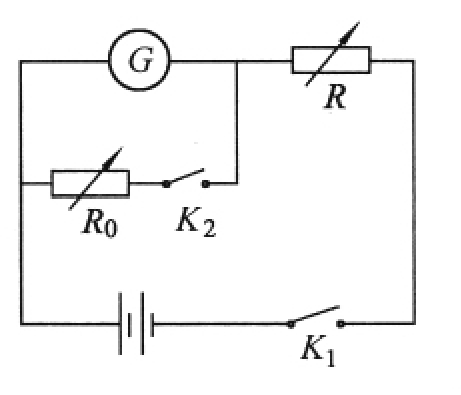
实验的过程是这样的：接通电键K₁调节可变电阻R直到被测电流计G满偏；接通电键K₂，保持R不变，调节电阻箱R₀，直到电流计半偏，若调节R。过程中电路中总电流可认为不变，则电流计内阻r_g等于R₀。可见，为保证测量在“纯化”的条件下进行，必须使电路中的总电流保持不变。具体的方法有两种：一种是使电流计内阻远小F变阻器电阻，即r_g《R，这样，当接通电键K₂和改变电阻箱R₀的阻值时，电路中的总电流基本不受影响（根据一般实际实验中所用电源电动势值及电流计的量程，这个条件总是能满足的，但教学中对条件的分析仍是必须强调的）；另一种是在电路中串联一只监测电流计G₀，如下图所示，当接通电键K划成本后，反复调节R和R₀，使总电流保持不变而被测电流计半偏，这样就能使R₀的阻值“准确”地（从原理上来说）等于被测电流计的内阻‰这两种方法各有特点：前一种方法强调了实验中近似处理的意义；后一种方法强调了理论上的严密性，但操作的难度较高。总之，这两种方法都是很有价值的。

善于改变实验的条件

利用改变实验条件的方法来揭露所研究的物理过程各个方面的特征，找出各个方面因素之间的关系，是实验研究的一种基奉思想和做法。

例如，为了认识电磁感应现象，我们先比较导体静止在磁场中和导体与磁场做相对运动这两种情况，再比较导体在磁场中向各个不同的方向运动的情况，由此认识到导体做切割磁力线运动时能产生感应电流。为了获得更全面的认识，再将两个线圈保持相对静止，使其中…个线圈通有电流，当这个电流改变时，另一个线圈中也产生感应电流。经过反复比较，我们终于认识到，穿过闭合电路磁通量的变化，足产生感应电流的普遍条件。

又如，为了认识光在两种透明媒质界面上发生的现象，我们先让光以不同的入射角从光疏媒质射向光密媒质。通过比较可以发现：不论以什么入射角入射，总是同时发生反射和折射现象；反射角和折射角都随入射角的增大而增大，反射光的强度随入射角增大而增强，折射光的强度随入射角的增大而减弱。再让光以不同的入射角从光密媒质射向光疏媒质，可以发现：当入射角较小时，也同时发生反射和折射现象，除了折射角大于入射角外，其余和光从光疏媒质射向光密媒质时相同；但当入射角大到一定值时，发生了全反射现象。

通过反复比较，最终对光在两种媒质界面上发生的现象有了全面的认识。只有通过在不同条件下对物理对象或物理过程的观察和比较，也就是说，在运动、变化中而不是在静止状态下来考察研究的对象，我们才能对研究对象的特点和本质有比较全面和深入的认识。

对于有多个因素起作用的物理过程，为了便于找出过程的规律，通常的做法是每一次都先控制几个因素不变而只改变某一个因素，这样依次考察各个因素对物理过程的影响，最后再用适当的数学方法进行归纳、总结。这种方法是大家比较熟悉的。

例如，研究物体的加速度与物体的质量及物体所受外力的关系，通常是分别研究物体的质量不变时加速度随外力的变化情况，以及物体所受的外力不变时加速度随物体质量的变化情况，然后进行综合。又如，研究气体的状态参量压强、体积、温度的关系时，是先分别研究等温过程中压强和体积的关系、等容过程中压强和温度的关系、等压过程中体积和温度的关系等，然后通过一定的数学处理，得到了气体的状态方程。这里，除了要注意研究的基本思想外，还应认真地体会实际实验过程中是如何实现条件控制的。

例如，研究等容过程中压强随温度变化的规律时，应该注意，在操作过程中，当温度变化时，是如何使气体的体积回到原先的值，然后才测量气体的压强的。又如，研究单摆的振动规律时，应该条理分明地按摆长、摆球的质量相同而振幅不同，摆长、振幅相同而摆球的质量不同，摆球的质量、振幅相同而摆长不同等情况来比较两个单摆的周期，最后得到结论：小振幅的条件下，在摆球质量、摆的振幅和摆长等因素中，单摆的周期只与摆长有关。当然，在实验研究中的这种改变单因子的做法也不是绝对的，因为在有些过程中，当一个因素变化时，往往不可避免地引起其他因素的变化，因而很难把各个因素完全隔离开来。这时，仍然能用一定的方法找到这些过程的规律，但实验数据处理就比较复杂的。

熟悉测量物理量常用的基本方法

物理量的测量是实验活动的基本内容，也是实验中工作量最大的，而且物理学中许多新现象的发现，都是和测量仪器及测鹫方法的改进分不开的。

物理学史上经典的物理量的实验，比较有代表性的如卡文迪许测定万有引力恒量的实验。卡文迪许实验的巧妙之处是用测量悬丝扭矩代替了对引力的直接测量。该实验的全部仪器放在特制的室里，而用望远镜进行观测，从而借助光杠杆对读数进行了放大，并且避免了气流的干扰；同时，这种设计还有利于平衡抵偿周围物体的作用。

卡文迪许的实验，开创了被人们称为“弦丝挂，火漆封”的精微测量技术。所谓“弦丝挂，火漆封”，就是用弦丝悬挂的扭摆做检测器，将其放在火漆密封的玻璃罩里，在减少外界干扰的条件下进行精微的观测。在卡文迪许实验室里，靠这套精微技术曾培养出如麦克斯韦、瑞利、卢瑟福等世界闻名的科学家，这些人曾被人们冠以“蜡封细绳派”的美名。

在18—19世纪的200年里，这套技术为物理学做出许多成果。例如，列别捷夫的光压测定、密里根的助手为测定电子电荷而进行的空气粘滞系数的测定、爱因斯坦关于磁矩与机械矩的测定、关于阿伏加德罗常数的测定等，用的都是这种技术。

据物理学史著作中描述，当时的科学家们为了安装一只悬丝扭摆，亲自烧熔石英，趁热拽拉，拔出的石英丝在室内纷纷飞扬；地上铺着黑色的天鹅绒地毯，落在其上的石英丝层见叠出，人们匍匐着、爬着，找出适宜的石英丝，安上小镜子，装配调整进行观测。实验家以能亲手配制这样一套仪器而引以为荣。英国物理学家瑞利曾经告诫后代，对于要进入研究之门的新学者，一定要先经受“弦丝挂，火漆封”的培训。

在现代物理中，随着人们研究的深入，对物理量测量的要求愈来愈高。例如，电子的正常磁矩，根据经典理论是一个玻尔磁子，即p₀＝le/2mc，而精密测量的结果是

p₁＝（1.001159652359±0.000000000031）e/2mc

根据量子电动力学计算，准确到6级电磁作用修正后的数值是p₁＝（1.001159652359士0.000000000280）e/2mc

这里p₁与p₀/2mc之差，即所谓反常磁矩。量子电动力学的理论值与实验值极好地相符，说明量子电动力学理论的正确性。可以设想，如果实验的基本误差超过1/1000，则电子的反常磁矩就不可能被观测到了。

因此，物理量的测量，不仅是一个技术E的问题，而且更具有方法论上的意义。

对于物理学中可以直接测量的物理量如质量、长度、时间、电流强度、电压等，首先要根据被测物理量的特点、大小及测量精度的要求，正确地选择测量仪器和仪器的量程以及在测量中控制测量条件的方法。关于仪器的选择，在测量一条百米跑道的长度时可以用带厘米刻度的卷尺，而测量一根头发的直径就必须用最小刻度为0.01mm的螺旋测微器；测量量热器中的水温时可以用水银温度计，而要测量炉温则必须用热电偶温度计；测量导体上的电压、电流时，所用伏特计、安培计的量程必须大于被测的量，但又不宜超过很多；用欧姆表测量导体电阻时应选择它的倍率，使被测电阻尽量在欧姆表表头刻度的中值附近，等等。每个物理量的测量，都必须在一定的条件下进行。例如，测量单摆的摆长，就必须在摆自然悬垂的状态下进行；在测量固体比热的实验中，当加热后的被测物体投入量热器后，液体的末温应该在液温上升到最高、恰好将开始下降时来读取，等等。许多测量仪器的原理、结构都有十分巧妙的构思，因此这些仪器的结构原理及调整和使用方法都能给我们很好的启发。

例如，游标卡尺，利用简单的游标就将长度测量的精度提高了很多。这个方法还可以用在其他物理量的测量中。例如，在分光计上，人们就用这种方法来提高角度测量的精度。甚至在时间的测量上，人们也用这种方法来提高测量的精度。我国的中央授时台，每分钟发出61个声信号，与每秒发出一次声响的天文摆钟构成一个“时间游标”，使分度值达到δt＝1/60s＝0.0166s，就是一个有趣的例子。

实际上，大多数的物理量是不能或不便直接测量的，只能将这些量转变为可以直接测量的物理量，然后利用这些待测量和这些直接测量的量之间的函数关系求得待测的量。另外，还常有一些现象，因不明显而不易观察或者不易直接观察，这时就要借助于力、热、电、光、机械等之间的相互转换，以间接地达到可观察、容易观察或观察效果明显的目的。

这里所说的转换，主要是从效果相当的思想出发进行的转换。这是物理实验中的重要思想方法，可以叫做转换法。例如，迈克尔逊干涉仪把测光速转换成测光的干涉条纹；导体的电阻是不便于直接测量的，可以通过测量加在导体上的电压和通过导体的电流，然后根据R＝U/I来求得导体的电阻，这就是伏安法测电阻；材料的密度是不能直接测量的，可以分别测量物体的体积和质量，然后根据p＝m/V来求得材料的密度；利用冲击摆测量弹丸的速度，弹丸射入冲击摆后二者的共同速度是很难测准的。

如果实验中用的冲击摆带有记录摆动最大偏角的指针的话，则可以测出冲击摆的最大偏角θ及摆长L，由式h＝L（1cosθ）求得摆的上升高度h，然后根据公式v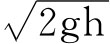＝求得摆的初速度；在测量重力加速度时，可根据单摆的周期公式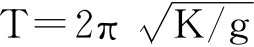测定单摆的摆长和周期，然后求得重力加速度。

关于电场强度的测定也是这样。电场强度的定义是E＝F/q，但实际上很难测准一个检验电荷的电量及其在静电场中受到的力，而电势差却能用电压表、电势差计或静电计等很方便地测得。如果所研究的电场可看做匀强电场的话，就可以测出两板之间的距离和电势差，然后根据E＝U/d来求得电场强度。因此，如果我们注意一下就会发现，一台无线电接收机的灵敏度总是用100μV/m这样的形式来表示电场强度的。

关于物理量的间接测量，应该强调的，首先是测量的原理，其次是实际的测量方法，包括仪器的选择和测量时应保持的条件。例如，用伏安法测电阻，必须根据被测电阻的估计值恰当地选择电压表和电流表的量程，测量时还必须保证电压表和电流表的读数同时读出。在间接测量中，还必须使各个直接测量的量的测量精度能互相匹配，要估计各个直接测量的量中哪一个对最后的结果影响最大，正确选择测量仪器和方法，把这个量测准。

例如，根据式R＝ρL/S来测量一条导线材料的电阻率，导线的长度用带毫米刻度的直尺测量，误差一般只有千分之几，而导线的直径一般只有零点几毫米，即使用螺旋测微计来测量，误差也可能达到百分之几，所以在电阻率的计算中，首先应保证直径测量的精确度。在实际测量中，要求在导线的几个不同部位从不同方向测定多个直径的读数，然后求它们的平均值。又如，在用单摆测量重力加速度的实验中，摆长是从摆的悬挂点量到摆球的中心。因为悬线的长度是用直尺测量的，摆球的直径就没有必要用游标卡尺来测量了。

在实际测量中，可以利用一块三角板测出悬挂点到摆球的下沿的距离L′和到摆球的上沿的距离L″，然后由式L＝（L′＋L″）/2求出摆长L。

考虑到测量悬挂点到摆球上沿距离时容易把线“抻”长，也可以先量出摆球的直径d，然后根据式L＝L′－d/2求得摆长L。而在单摆摆长和周期两个量的测量中，如果摆长取1m红右，则摆长测量的误差可以很容易地控制在1/1000左右；而如果用秒表来测量时间，考虑到操作者的反应时间有零点几秒昀误差，而且在重力加速度的计算公式中，周期是以平方的形式出现的，为了使周期的测量精度和摆长的精度相匹配，就必须测出单摆摆动的多个周期的总时间。

物理实验中消除误差的巧妙方法

物理实验中有许多方法可以用来消除误差，如交替法、替代法、补偿法、累加法等。

（1）交替法。

用天平测量物体的质量，由于天平的两臂不绝对等长而存在系统误差。这种误差可以用下面的方法来解决：先将物体放在天平左盘，加减砝码到天平平衡后记下测量的读数为m₁；再将物体放在右盘，加减砝码到天平再一次的平衡后，记下测量的读数为m₂；则被称物体质量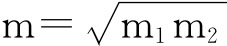。这样，就把天平两臂不等长造成的误差消除了。这就是所谓的“交替法”这是就原理来说的。

在实际计算中，由于m₁和m₂相差很小，而有。

这种交替法还可以用在用滑线电桥测电阻的实验中。在滑线电桥中，电阻线不可能是绝对均匀的，电阻线长度的测量也不可能绝对准确，这样带来的误差一般都要比标准电阻的误差大得多。

消除这种误差的方法是先尽可能准确地将滑动触点固定在电阻线中点，将被测电阻和电阻箱分别接在电桥的两臂，调节电阻箱阻值直到电桥平衡，记下电阻箱读数风；交换被测电阻和电阻箱的位置（电阻线的滑动触点不动），调节电阻箱阻值直到电桥再一次平衡，记下电阻箱读数为R₂。

很容易证明，被测电阻的阻值。这样就消除了上述原因造成的测量误差。

（2）替代法。

消除上述天平和电桥测量中的误差还可以用另外的方法，如替代法。当用天平称量物体时，和普通的做法一样，在天平的一盘放上物体，加减砝码直到天平平衡；然后取下物体，用砝码来代替被测的物体，在另一盘加减砝码直到天平重新平衡，则取代物体的砝码的质量就等于被测物体的质量。

这样，也消除了天平两臂不等长造成的误差。这种方法可以叫做“替代法”。替代法也可用在用电桥来测量电阻中，即先将被测电阻和另一个定值电阻（其阻值尽可能与被测电阻接近）分别接入电桥的两臂，移动滑动触点到电桥平衡；固定滑动触点，用电阻箱代替被测电阻，调节电阻箱的阻值直到电桥重新平衡，此时电阻箱的阻值就是被测电阻的阻值。

（3）补偿法。

实验中还常常用“补偿法”来消除某些原因造成的系统误差。例如，在测量固体比热的实验中，当经过加热的被测物体投入量热器后，由于量热器内的温度高于量热器外环境的温度，因此会有一部分热量散失到空气中，造成实验的误差。如果要进行较精密的测量，则可以根据粗测的情况估计物体投入量热器以后液体上升的温度；进一步测量时，先使液体的初温适当低于环境的温度，而使末温高于环境的温度。

例如，估计液温将上升10℃，则可使初温比环境温度大约低5℃，这样末温将比环境温度大约高5℃，整个过程中量热器向空气吸热和放热量就可基本抵消了。

（4）累积法。

“累积法”是在一些微小量测量中常用的方法。例如，前面提到的单摆周期的测量，还有实验中将细导线缠绕在木棒上测出若干圈导线所占的长度，然后求出导线的直径等，用的都是这种方法。“累积法”使得在仪器等级相同的条件下的测量精度大大提高了。