古希腊数学学派

第二节　古希腊数学学派

古希腊数学是在先后相继几个中心地点发展起来的，每个中心地点，总是由一两个伟大学者组织成群的学者开展学术活动，为数学大厦的筑起添砖加瓦。用现在的语言描述，乃为创建学派，师徒相传，推动数学的发展与传播。

一、爱奥尼亚学派

这个学派是由泰勒斯创建的。泰勒斯早年跟随父亲从商，由于贸易往来，有机会游访埃及、巴比伦等国家和地区，在游访期间，被当时兴旺发达的外地文化所吸引，萌发兴趣，开始倾心学习和研究天文、几何知识。被誉为“古希腊七贤人”之首。

数学与哲学联系，尤其是在古代，很多数学家都懂得一定的哲学知识，正像我国古代的数学家一般都懂得历法知识一样，泰勒斯也是一位哲学家。在他的学说里，首次对自然界进行脱离宗教的解释，他认为水是万物之源，一切都是由水形成的，一切事物的本质都依水的状态而改变。结论是，植物的生命保存在它的汁液里，因为植物干燥了就会死；动物的生命保存在血液里，甚至火焰也要吸取湿润。

根据现存原典史料证明，泰勒斯是古希腊的第一位天文学家。由于他准确地预言公元前585年5月28日的日食时间，使泰勒斯名声大振。据说古代两个奴隶制国家交战，5年未见胜负，泰勒斯扬言上天要制止战争，以某月某日必日食来作警告。果然到了那一天，两军正在酣战不停，突然太阳失去光辉，百鸟归巢，明星闪烁，白昼顿成黑夜。双方士兵将领大为恐惧，于是停战和好，后来两国还互通婚姻。

泰勒斯创建的学派——爱奥尼亚学派对数学的发展起到了很大作用，尤其对几何学的发展，起到的作用更大。有人认为泰勒斯是数学历史上第一位几何学家。

根据欧几里得《几何原本》第一卷的注释者普罗克洛斯记载的史料，充分说明了泰勒斯学派确立和证明了为人们所公认的第一批几何定理。这种记载源于希腊数学史家欧德莫斯所著《几何学史》，遗憾的是这部著作已经失传。

根据普罗克洛斯记载，泰勒斯至少证明了如下几个命题：

（1）圆被任一直径所平分。

（2）等腰三角形的两底角相等。在古代，曾把角相等称作“相似”。

（3）两条直线相交，对顶角相等。

（4）两个三角形两角与所夹边对应相等，则两个三角形全等。有人证实泰勒斯曾利用这条定理测定海上两船间的距离。

泰勒斯是用如下简单的方法测量的：

假设：A，B是两条船，可望而不可及。在岸上引AC垂直于AB，D是AC的中点，过C点向AB相反方向，引CE垂直于CA（使B，D，E在同一条直线上）这时，CE和AB距离相等，CE是可直接测量的。

根据希腊历史学家普鲁塔克的记载，泰勒斯曾应用两个等角三角形对应边成比例的定理，测出金字塔的高度。具体做法是将一根标杆竖立在平地上，利用塔影长与标杆影长的比，等于塔高与标杆高的比，来算出塔高。也有的学者说泰勒斯是根据当标杆影长和标杆长相等时，塔高与塔影也相等的道理推得的。有人认为这两种说法都有不妥之处。

根据有的史料记载，泰勒斯还发现了“半圆上的圆周角都是直角”的命题，但是，也有的史料指出了这个命题在巴比伦的数学中已经出现了，它与计算弦到圆心的距离有关系。而其证明应属泰勒斯。

从以上可以看出，泰勒斯学派并不满足于知其然，还要追求所以然的道理。他迈出了对数学命题证明的关键一步，为平面上线与角的理论奠定了基础，把科学的方法渗透于数学真理之中，载入数学史册。这标志着人们对客观事物的认识从感性上升到理性，这在数学发展史上也是一个重要飞跃。因为数学中的逻辑证明，能保证命题的正确性，使理论立于不败之地，令人深信不疑，也能揭示出各定理间的内在联系，使数学构成严密的体系。

二、毕达哥拉斯学派

这个学派是以贵族式的观念形态作为基础，与在当时撒摩斯岛的古希腊民主制的观念形态，形成尖锐的对立，是具有神秘色彩的组织。领头人毕达哥拉斯生于撒摩斯岛。关于毕达哥拉斯本人有很多传说，甚至很难判断哪些传说是符合实际的，哪些是虚构的。就连他的生卒年月也很难确定。

毕达哥拉斯年轻时期，游历了很多地方，特别是游访古埃及和古巴比伦等地，学习了一些数学知识，大约在公元前530年回国，开始组建学派。这个学派的主张和观念曾引起撒摩斯公民的不满情绪，毕达哥拉斯为了避开人们的舆论，只好离开自己出生的本土，逃往希腊的移民区阿佩宁半岛，并定居在克罗托那城，重新建立学派。由于毕达哥拉斯参与政治活动，后来被杀害。他死后，其门徒散居到希腊其他学术中心，继续传授他的教诲，达200年之久。

毕达哥拉斯首先研究了数学的抽象概念，希腊学者亚里士多德曾说，毕达哥拉斯学派把数看作是真实物质对象的终极组成部分。数不能离开感觉到的对象而独立存在，即早期毕达哥拉斯学派认为一切对象由（整）数组成，或者说数乃宇宙的要素。因为他们心目中的数就如同我们心目中的原子一样，把数看作是现实的本源，是严谨性和次序性的根据，是在宇宙体系里控制着天然的永恒关系，企图用数来解释一切。甚至认为万物都包含数（整数），且万物也都是数（整数）。对周围观察到的现象，也都是用数的关系来说明。例如，当听到悦耳的音乐时，觉察到“和声”谐音，毕达哥拉斯学派认为只能用3根弦才能发出此音，其长度之比为3∶4∶6，并在很多场合，也都发现这种比例关系，立方体的面数、顶点数、棱数的比为6∶8∶12。

由于毕达哥拉斯学派赋予数如此重大的意义，因此，毕达哥拉斯学派非常注意研究数，也就是开始研究数的理论，研究数的性质，而注重实际的计算。

毕达哥拉斯学派首先使用了更加方便的记数系统，采用了腓尼基人所用的希腊字母表中的字母，并增加某些腓尼基的字母来表示数。

毕达哥拉斯学派还依据几何和哲学的神秘性来对“数”进行分类，按照几何图形分类，可分成“三角形数”“正方形数”“长方形数”“五角形数”等等。

实际上，以上各种类型的象形数，可从等差级数和导出来。

1＋3＋5＋……＋（2n－1）＝n²（正方形数）

2＋4＋6＋……＋2n＝n（n＋1）（长方形数）

例如，正方形数的图形可分为小正方形和曲尺形，反复分割，小正方形内一点和曲尺形内点的和，即是奇数系列之和：1＋3＋5＋……

毕达哥拉斯学派还把“数”分成“完全数”和“相亲数”。如果一个数除其本身外的所有因数的和等于这个数，那么这个数就叫“完全数”。例如，6是完全数，因为它的每个因数之和为6，即：6＝1＋2＋3。若两个数中每个数的因数的和等于另一个数，这两个数叫做“相亲数”。按此定义，220和284是相亲数。因为220的因数之和为：1＋2＋4＋5＋10＋11＋20＋22＋44＋55＋110＝284，而284的各因数之和为：1＋2＋4＋71＋142＝220。毕达哥拉斯学派还声称：“谁是我的朋友，就应该像数220和284一样。”

毕达哥拉斯发现了著名的“勾股定理”。但是，在什么情况发现的？怎样证明的？说法不尽一致。普罗克洛斯在注释欧几里得《几何原本》第1卷题47时，说得也不明确，指出在古代历史上有各种传说，据说这个定理是毕达哥拉斯发现的，毕达哥拉斯为了庆贺自己的业绩，杀了一百头牛。普洛塔克也有类似的说法，指出毕达哥拉斯是用填加面积的方法证明“勾股定理”的。

在直角三角形中，两条直角边分别为a，b，斜边长为c，以a＋b为一边画正方形，这样，在此正方形中，含4个直角三角形、一个以a为边的正方形和一个以b为边的正方形。

另外，再画一个以a＋b为边长的正方形，经过分割，这个正方形含有4个直角三角形和1个边长为c的正方形。因为两个正方形（即（a）和（b））面积相等，各减去同样的4个直角三角形的面积，立刻得到：

a²＋b²＝c²

实际上，毕达哥拉斯学派发现“勾股定理”之后，很容易过渡到对新数——无理数的发现，但毕达哥拉斯学派认为这违背了他们的信条（世界上一切都是由整数和整数之比构成），相传毕达哥拉斯学派成员在海上游玩，把无理数的宣传者希帕索斯推到波涛汹涌的大海里。希腊人称不可公度量之比为αλoγos，当时，人们都在回避这种量，导致了数学史上的第一次危机。

毕达哥拉斯学派还研究了关于正多边形和正多面体的作图问题，尤其是首先完成了正五边形的作图，为解决正多边体的作图问题奠定了基础。毕达哥拉斯学派曾作出了当时所有可能的正多面体：具有4个等边三角形面的正四面体，具有8个等边三角形面的正八面体，由20个正三角形围成的正二十面体，由6个正四边形围成的正六面体，由12个正五边形围成的正十二面体。毕达哥拉斯学派认为这些都是“宇宙图形”，将四面体称为火；八面体称为气；二十面体称为水；六面体称为土；十二面体称为宇宙。他们认为在整个几何体中最优美的是球。

毕达哥拉斯学派在对数学的发现中，不断追求“美”的形式。他们认为日、月、五星都是球形，浮悬在太空中，这是最完美的立体，而圆是最完美的平面图。就是曾被誉为“巧妙的比例”，并染上各种各样瑰丽诡秘色彩的“黄金分割”也是这个学派首先认识到的。

综上所述，使我们认识到，毕达哥拉斯学派对于研究解决数学问题的方法，发挥了很大作用。他们规定在数学中必须坚持严格证明，对数学的发展具有特殊意义。

三、诡辩学派

“诡辩”一词含“智慧”之意，诡辩学派也译作“哲人学派”或“智人学派”。

诡辩学派主要是以讲授修辞学、雄辩术、文法、逻辑、数学、天文等科为职业，也经常出入群众集会场所，发表应时的演说等，其代表人物是普洛塔哥拉斯、哥尔基亚、安蒂丰等。

值得注意的是，数学历史中著名的“三大几何难题”的研究始于诡辩学派。“三大几何难题”虽然不能精确求解，对其研究和探索，却引出了大量的数学发现。

（1）倍立方问题，即求作一立方体，使其体积是一已知立方体的2倍。

关于这个问题的产生众说纷纭。其中有一种说法是，在第罗斯岛上，瘟疫不断蔓延，岛上的人求教于巫神，巫神告诉他们应把现有立方祭坛加倍。这就产生了“倍立方问题”，也称“第罗斯问题”。

这个问题，实际上是已知立方体的边长为a，求作边长为x的立方体。

诡辩学派试图利用直尺（没有刻度）和圆规作出图形，据说希腊毕达哥拉斯学派的希波克拉底曾把倍立方问题归结为求线段a与2a之间的两个等比例中项，不妨用现代数学符号表示，设x，y为两个比例中项，有：

a∶x＝x∶y＝y∶2a

由（1）和（2），消掉y，则：x⁴＝2a³x，

∴x³＝2a³即为所求。

虽然希波克拉底没能根据所谓“几何作图法”（只用没有刻度的直尺和圆规，分别只能画直线和圆）求出x、y，但是他把立体问题转化到平面中来解决，这种思考方法是难能可贵的，是希波克拉底的重要贡献，为后人用二个矩（直角尺）作出a与2a两个等比中项奠定了基础。

倍立方问题虽然不能精确求解，但希腊人对它的研究与探索，推动了数学的发现。例如，门奈赫莫斯给出了这个问题的两种解法，由此发现了圆锥曲线。下边简述门奈赫莫斯的解法：

①作两条有公共顶点的、其轴互相垂直的抛物线，并且使得其中一个的正焦弦为另一个的2倍。设x表示从两条抛物线的另一个交点向较小的抛物线的轴所作垂线之长。于是，以x为边的立方体的体积等于以较小的正焦弦为边的立方体的体积的2倍。

②作一正焦弦为s的抛物线，然后作一横截轴等于4s且以抛物线之轴为其渐近线的等轴双曲线，并且过抛物线顶点作其切线。设x为从两条曲线的交点向抛物线的轴所作垂线之长，则x³＝2s³。

另外，狄俄克利斯在解决这个问题时，发现了蔓叶线。

（2）任意角三等分问题。

按希腊时期几何作图法的要求，①直尺只能做连接两点的直线之用；②圆规只能做画圆之用，不许作分度计或量长度之用。在这两个条件限制下，任意角三等分是不可能的。

希腊学者把任意角三等分问题归结为斜向问题，对它研究与探索，发现了蚌线等等。

如果没有几何作图法的限制，任意角三等分问题当然可以解决，三等分法有几十种之多，不妨举一个例子。

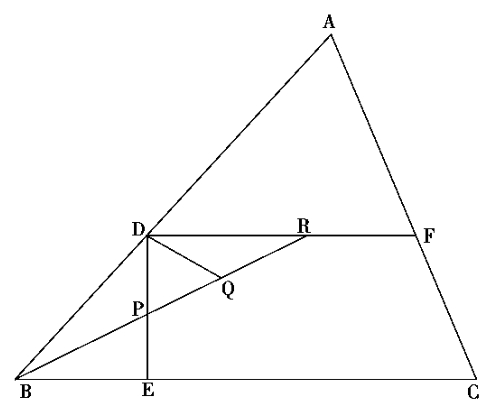
在已知∠ABC的一边AB上，取一点D，引DE垂直于BC，DF平行于BC，取一直尺，上面刻上三点P，Q，R，且PQ＝QR＝DB，直尺通过点B（DE过点P，DF过点R），由此，△PDR是直角三角形，且Q是斜边PR之中点，PQ＝DQ＝RQ，∴∠DQB＝2∠BRD，又∵PQ＝QR＝DB，∴DQ＝DB，∴∠DQB＝∠DBQ。另外，DF∥BC，∴∠BRD＝∠RBC，故∠DBQ＝2∠RBC，直线BR是∠ABC的三等分线。

从上面的作法都能将任意角三等分，但是，已经突破了希腊时期的“初等几何作图法”的要求。

若用代数思想解释这两个古老问题，也是很清晰的。实际上，倍立方和任意角三等分问题，都是属于求解三次方程问题。直尺画出的直线可表示为一次方程

ax＋by＋c＝0

而用圆规画圆，其方程可表示为二次方程

x²＋y²＋ax＋by＋c＝0

仅用直线和圆构成的图形是不能求解三次方程的。因此，用初等作图法解决如上两个问题是不可能的。

（3）化圆为方问题。即：求作一正方形，使其面积等于一已知圆。

远在公元前1800年，古代埃及人就取正方形的边长等于给定圆的直径的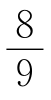的方法“解决”这个问题。后来，有成千上万的人对这个问题进行过研究，并且尽管已经证明了用欧几里得工具作此图的不可能性，但时有号称成功“化圆为方者”的出现。

希腊时期的希波克拉底成功地求出了某些特殊的由两个圆弧围成的月形面积，当然没有解决化圆为方问题，但确实解决了一个有关的问题。设ABC是一等腰三角形，并设它内接于中心为O的半圆，设AEB是以AB为直径的半圆。则有半圆ABC的面积∶半圆AEB的面积E＝AC²∶AB²＝2∶1，所以，OADB的面积等于半圆AEB的面积。现在把两者的公共面积ADB去掉，则有月牙形的面积等于三角形AOB的面积。

上边的例子说明希波克拉底从探索曲边形面积与直边形面积相等的思路，试图来解决“化圆为方”的问题。

希波克拉底另一个月形求积问题是，设ABCD等于以AD为直径的圆的内接正六边形的一半。作该圆与以AB为直径的半圆之间的月形。试证明：梯形ABCD的面积等于该月形面积的3倍加上以AB为直径的半圆的面积。

若取消作图工具的限制，“化圆为方”问题也是可以解决的。欧洲文艺复兴时代的大师达·芬奇曾创建用圆柱来解决化圆为方问题的巧妙方法。

2000多年来，“三大几何难题”显现出经久不息的魅力，无数具有聪明才智的有志之士曾做出不懈的努力，都未如愿以偿。直到1637年，法国数学家笛卡儿创建解析几何，尺规作图的可能性才有了准则。1837年，数学家凡齐尔给出了“倍立方”“任意角三等分”不可能性的证明。1882年，数学家林德曼证明π的超越性，“化圆为方问题”的不可能也得以确立。1895年，克莱因给出了三大几何难题不可能用“初等几何作图法”解决的简单而明晰的证明，彻底解决了2000多年的悬案。

值得注意的是，随着人们对“几何三大难题”的研究，激发了人们对数学新概念的研究和探索，例如，对圆锥曲线，三、四次代数曲线及割圆曲线等等的发现，就是在寻求解决“几何三大难题”中迎刃而解的。对数学理论的发展，也是有重要作用的。譬如，在对“化圆为方”的研究中，希腊学者安蒂丰先作圆内接正方形，将边数加倍，得内接正八边形，再加倍，得正十六边形，这样继续下去，最后的正多边形必与圆周相合。也就是多边形与圆的“差”必会“穷竭”，于是可以化圆为方了。结论虽然是错误的，但提出了一种有重要价值的“穷竭法”，它是近代极限理论的雏形。

四、厄勒亚学派

这个学派主要活动在厄勒亚地区，主要代表人物是芝诺。他首次用量的观点揭示运动中的矛盾，提出了4个违背运动常识的悖论。芝诺提出4个悖论的目的尚需进一步探索。而其背景是，当时人们对空间和时间有两种对立的看法：一种认为空间和时间无限可分，这样，运动则是连续而平滑的；另一种认为空间和时间是由不可分的小段组成的，这样，运动则是一连串的小跳动。芝诺的悖论是针对这两种理论的，他的关于运动的4条悖论的前两条是反对第一种学说的，而后两条是反对第二种学说的。我们不妨简略地考察一下4条悖论。

（1）二分法说：认为运动不存在，因为一个物体从A到B，首先要通过AB距离的一半，但要通过一半，必须通过一半的一半，如此下去，认为此物体永远不能到达B地。

也有人把芝诺的悖论理解为：要通过有限长度就必须通过无穷多的点，这就意味着必须到达没有终点的某种东西的终点。

（2）追龟说：据说在希腊有一位快走如飞的阿基里斯，芝诺认为他永远追不上步履迟钝的龟。譬如说，阿基里斯以10倍的速度追逐距离他100米处爬行的龟。当阿基里斯走100米时，龟爬了10米，当阿基里斯走10米时，龟又爬了1米，如此下去，这样永远相隔1小段距离，所以，总也追不上。

实际上，这个问题用极限方法可以马上得出结论。他（它）们走过何处阿基里斯能追逐到龟。

（3）飞箭静止说：芝诺认为飞箭在任一瞬间必在一确定位置，因而是静止的，于是，所谓运动不过是多个静止点的总和。

（4）运动场论：两组个数相同的物体沿跑道相向移动，一组从终点出发，而另一组是从中点运动，两者以相同速度移动，芝诺认为一半的时间和整个时间相等。

按照芝诺提出的观点，设有甲、乙、丙三排运动员，并设在单位时间内，乙排往左移动一步，而丙排则往右移动一步，于是相对于乙排而看丙排就移动了两步。因此使丙向右方移动一步所需的时间为半个单位，所以半个时间单位等于一个时间单位。

悖论思想不仅在运动方面存在，而且渗透到社会领域。相传在远古时期就曾产生过悖论。据说一个残忍的国王，下令不许外地人进入他的领地，否则就要处以死刑。并规定进入他的领地若说真话，要处以砍头罪，若说假话处以淹死罪。一天，一个聪明的外地农民大摇大摆地进入了他的领地，说：我是来被淹死的。守卫领土的士兵无法处刑，如果认为他说的是真话，应处以砍头罪，如果一旦执行，他的话便是假话。如果认为他说的假话，应处以淹死罪，一旦执行，他的话又变成真话。这样，使国王也束手无策，只好放走农民。这说明悖论思想充满了矛盾，需要我们认真研究与探索。

芝诺在描述运动中，产生了悖论思想，实际上，芝诺的认识已经接近极限观念的边缘，但他最终还是否认了运动的真实性，没能认识极限。值此，应该认识到，悖论思想给数学界以极大的影响，直到集合理论建立时，仍余波未尽。

五、柏拉图学派

这个学派是继诡辩学派之后兴起的。其主要代表人物是柏拉图，他年轻时曾跟随希腊哲学家苏格拉底学习哲学，受到逻辑思想影响，而后成为雅典举世瞩目的大哲学家。柏拉图在雅典建立了自己的学派，对其哲学思想的产生和扩大影响具有重要意义。柏拉图从毕达哥拉斯学派吸收了许多数学观点，并运用到自己的学说中，因此，柏拉图的哲学提高了对数学科学的兴趣。他认为，不知道数学的人，不可能接受哲学知识，充分认识到了数学对研究哲学和宇宙的重要作用，并积极鼓励自己的朋友、学生学习和研究数学。据说，在他的学园门口写着：“不懂几何者不得入内。”

柏拉图在其著作《共和国》中，曾强调：我们必须竭力奉劝我国未来的主人学习算术，不是像业余爱好者那样来学，而必须学到唯有靠心智才能认识数的性质那种程度；也不像商人和小贩那样，仅是为着做买卖去学，而是为了军事上的应用，为了灵魂本身去学的。（学习算术）是使灵魂从暂存过渡到真理和永存的捷径。我所说的意思是算术有伟大和崇高的作用，它迫使灵魂用抽象的数来进行推理，而厌弃在辩论中引入可见和可捉摸的对象……

柏拉图学派重视数学的严谨性，在教学中，坚持准确地定义数学概念，强调清晰地阐述逻辑证明，系统地运用分析方法和推理方法；例如，在推理中，假设已知所求未知数，再以这个假设为基础，得出已知量与未知量应当存在的关系式的结论，归根到底是化为求未知量。柏拉图学派把这种方法运用到作几何图形上。

在柏拉图思想的影响下，希腊学者重视对数学的学习和研究，出现了一批对数学发展作出贡献的数学家。例如，欧多克索斯曾是柏拉图的学生，他创造性地排除了毕达哥拉斯学派只能适用于可通约量的算术方法，用公理法建立比例论，欧几里得《几何原本》第五卷《比例论》的大部分内容是欧多克索斯的工作成果。

欧多克索斯曾证明了对近代极限理论发展起重要作用的命题，例如，“取去一量之半，再取去所余之半，这样继续下去，可使所余的量小于另一任给的小量。”他也曾提出过：“对任意两个正数a，b，必存在自然数n，使得na＞b”的重要命题。后来，在阿基米德的名著《论球和柱》中，给予了几何意义的阐述，在现代数学中，被誉为“阿基米德公理”。

柏拉图的另一位学生亚里士多德是吕园学派的创始人和领导者，被誉为形式逻辑的鼻祖，其思想影响西方数千年，他也非常重视数学的学习和研究，他所给出的点、线、面、体的定义，广为传播。他还应用演绎逻辑的方法对许多数学问题作出了证明。

柏拉图学派主张科学的任务是发现自然界的结构，并把它在演绎系统里表述出来，首次提出了应该把严格推理法则系统化，从而为数学走向新的阶段起到了前导作用。

综上所述，我们列举了希腊时期的几个学派的工作，以此来了解这个时期数学的发展。实际上，希腊学派的建立是推动数学发展和传播的重要因素，在数学历史中，产生很大影响。可谓创建学派的师徒相传，对数学发展产生莫大的推动力。