世纪数学问题欣赏

6.5.1 希尔伯特的23个数学问题

1900年8月6日这一天，巴黎圣母院的钟声迎来了数学界圣会——国际数学家大会，开幕式上，年方38岁的法国数学家大卫·希尔伯特(David Hilbert，1862～1943)走上讲台，第一句话就说道：“揭开隐藏在未来之中的面纱，探索未来世纪的发展前景，谁不高兴呢？”接着，他根据过去特别是19世纪数学研究的成果和发展趋势，向与会者及国际数学家大会发表了题为《数学问题》的著名演讲——提出了23个数学问题.这23个问题通称希尔伯特问题，后来成为许多数学家力图攻克的难关，对现代数学的研究和发展产生了深刻的影响，并起了积极的推动作用．希尔伯特问题中有些现已得到圆满解决，有些至今仍未解决．他在演讲中所阐发的相信每个数学问题都可以解决的信念，对于数学工作者是一种巨大的鼓舞．这一演讲，成为世界数学史上的重要里程碑，为20世纪的数学发展揭开了光辉的一页！

希尔伯特的23个问题分属四大块：第1到第6问题是数学基础问题；第7到第12问题是数论问题；第13到第18问题属于代数和几何问题；第19到第23问题属于数学分析问题．这23个问题是：

［01］康托的连续统基数问题．

1874年，康托猜测在可数集基数和实数集基数之间没有别的基数，即著名的连续统假设．1938年，侨居美国的奥地利数理逻辑学家哥德尔证明连续统假设与ZF集合论公理系统的无矛盾性．1963年，美国数学家科恩(P.Choen)证明连续统假设与ZF公理彼此独立．因而，连续统假设不能用ZF公理加以证明．在这个意义下，问题已获解决．

［02］算术公理系统的无矛盾性．

欧几里得几何的无矛盾性可以归结为算术公理的无矛盾性．希尔伯特曾提出用形式主义计划的证明论方法加以证明．1931年，哥德尔发表不完备性定理作出否定．1936年，根茨(G.Gentaen，1909～1945)使用超限归纳法证明了算术公理系统的无矛盾性．

［03］只根据合同公理证明等底等高的两个四面体有相等之体积是不可能的．

问题的意思是：存在两个等高等底的四面体，它们不可能分解为有限个小四面体，使这两组四面体彼此全等．德恩(M.Dehn)1900年已解决．

［04］两点间以直线为距离最短线问题．

这个问题是就一般情况而言的，满足这个性质的几何例子很多，因而需要加以某些限制条件．1973年，前苏联数学家波格列洛夫(Pogleov)宣布，在对称距离情况下，问题获得解决．

［05］拓扑学成为李群的条件(拓扑群)．

这个问题简称连续群的解析性，即是否每一个局部欧氏群都一定是李群．1952年，由格里森(Gleason)、蒙哥马利(Montgomery)、齐宾(Zippin)共同解决．1953年，日本学者山迈英彦已得到完全肯定的结果．

［06］对数学起重要作用的物理学的公理化．

1933年，前苏联数学家柯尔莫哥洛夫将概率论公理化．后来，在量子力学、量子场论方面取得成功．但对物理学各个分支能否全盘公理化，很多人有怀疑．

［07］某些数的超越性的证明．

需证：如果α是代数数，β是无理数的代数数，那么α^β一定是超越数或至少是无理数(例如， 和e^π)．前苏联的盖尔芳德(Gelfond)1929年、德国的施奈德(Schneider)及西格尔(Siegel)1935年分别独立地证明了其正确性．但超越数理论还远未完成．目前，确定所给的数是否超越数，尚无统一的方法．

［08］素数分布问题，尤其对黎曼猜想、哥德巴赫猜想和孪生素数问题．

素数是一个很古老的研究领域．希尔伯特在此提到黎曼(Riemann)猜想、哥德巴赫(Goldbarh)猜想以及孪生素数问题．黎曼猜想至今未解决．哥德巴赫猜想和孪生素数问题目前也未最终解决，其最佳结果均属中国数学家陈景润．

［09］一般互反律在任意数域中的证明．

1921年由日本学者高木贞治，1927年由德国学者阿廷(E.Artin)各自给以基本解决．而类域理论至今仍在发展之中．

［10］能否通过有限步骤判定不定方程是否存在有理整数解？

求出一个整数系数方程的整数根，称为丢番图(210～290，古希腊数学家)方程可解．1950年前后，美国数学家戴维斯(Davis)、普特南(Putnan)、罗宾逊(Robinson)等取得关键性突破．1970年，巴克尔(Baker)、费罗斯(Philos)对含两个未知数的方程取得肯定结论．1970年，前苏联数学家马蒂塞维奇最终证明：在一般情况下答案是否定的．尽管得出了否定的结果，却产生了一系列很有价值的副产品，其中不少和计算机科学有密切联系．

［11］一般代数数域内的二次型论．

德国数学家哈塞(Hasse)和西格尔(Siegel)在20世纪20年代获重要结果．20世纪60年代，法国数学家魏依(A.Weil)取得了新进展．

［12］类域的构成问题．

即将阿贝尔域上的克罗内克定理推广到任意的代数有理数域上去．这个问题仅有一些零星结果，距彻底解决还很远．

［13］一般7次代数方程以二变量连续函数之组合求解的不可能性．

7次方程x⁷+ax³+bx²+cx+1=0的根依赖于方程中的3个参数a、b、c；x=x(a，b，c)．这一函数能否用两个变量函数表示出来？这个问题已接近解决．1957年，前苏联数学家阿诺尔德(Arnold)证明了在［0，1］上任一连续的实函数f(x₁，x₂，x₃)可以写成形式 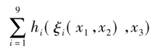，这里h_i和ξ_i为连续实函数．柯尔莫哥洛夫证明f(x₁，x₂，x₃)可以写成形式 ，这里h_i和ξ_i为连续实函数，ξ_ij的选取可以与f完全无关．1964年，维土斯金(Vituskin)推广到连续可微情形，对解析函数情形则未解决．

［14］某些完备函数系的有限的证明．

即域K上的以x₁，x₂，…，x_n为自变量的多项式f_i(i=1，2，…，m)，R为K［x₁，x₂，…，x_m］上的有理函数F(x₁，x₂，…，x_m)构成的环，并且F(f₁，f₂，…，f_m)∈K［x₁，x₂，…，x_m］，试问R是否可以由有限个元素F₁，F₂，…，F_N的多项式生成？这个与代数不变量问题有关的问题，日本数学家永田雅宜于1959年用漂亮的反例给出了否定的解决．

［15］建立代数几何学的基础．荷兰数学家范德瓦尔登于1938～1940年，魏依于1950年已解决．注：舒伯特(Schubert)计数演算的严格基础．

一个典型的问题是：在三维空间中有四条直线，试问有几条直线能和这四条直线都相交？舒伯特给出了一个直观的解法．希尔伯特要求将问题一般化，并给以严格基础．现在已有了一些可以计算的方法，这些计算方法和代数几何学有密切的关系．但严格的基础至今仍未建立．

［16］代数曲线和曲面的拓扑研究．

这个问题前半部分涉及代数曲线含有闭的分枝曲线的最大数目．后半部分要求讨论 的极限环的最多个数N(n)和相对位置，其中X、Y是x、y的n次多项式．对n=2(即二次系统)的情况，1934年福罗献尔得到N(2)≥1；1952年鲍廷得到N(2)≥3；1955年前苏联的波德洛夫斯基宣布N(2)≤3，这个曾震动一时的结果，由于其中的若干引理被否定而成疑问．关于相对位置，中国数学家董金柱、叶彦谦于1957年证明了E₂不超过两串．1957年，中国数学家秦元勋和蒲富金具体给出了n=2的方程具有至少3个成串极限环的实例．1978年，中国的史松龄在秦元勋、华罗庚的指导下，与王明淑分别举出至少有4个极限环的具体例子．1983年，秦元勋进一步证明了二次系统最多有4个极限环，并且是(1，3)结构，从而最终解决了二次微分方程的解的结构问题，并为研究希尔伯特第［16］问题提供了新的途径．

［17］半正定形式的平方和表示．

实系数有理函数f(x₁，x₂，…，x_n)对任意数组(x₁，x₂，…，x_n)都恒大于或等于0，确定f是否都能写成有理函数的平方和？1927年阿廷已肯定地解决．

［18］用全等多面体构造空间．

德国数学家比贝尔巴赫(Bieberbach)于1910年和莱因哈特(Reinhart)于1928年作出部分解决．

［19］正则变分问题的解是否总是解析函数？

德国数学家伯恩斯坦(Bernstein)于1929年和前苏联数学家彼德罗夫斯基于1939年已解决．

［20］研究一般边值问题．

这个问题进展迅速，已成为一个很大的数学分支．目前还在继续发展．

［21］具有给定奇点和单值群的Fuchs类的线性微分方程解的存在性证明．

这个问题属线性常微分方程的大范围理论．希尔伯特本人于1905年、勒尔(H.Rohrl)于1957年分别得出重要结果．1970年法国数学家德利涅(Deligne)作出了出色贡献．

［22］用自守函数将解析函数单值化．

这个问题涉及艰深的黎曼曲面理论，1907年克伯(P.Koebe)对一个变量的情形已解决，而使问题的研究获得重要突破．其他方面尚未解决．

［23］发展变分学方法的研究．

这不是一个明确的数学问题．20世纪变分法有了很大发展．

科学发展的每一个时代都有自己的问题，希尔伯特站在当时数学研究的最前沿，高瞻远瞩地用23个数学问题，预示20世纪数学发展的进程．现在，时光已过去了一百多年，这23个问题约有一半获得解决．一百多年来，人们把解决希尔伯特问题，哪怕是其中一部分，都看成是至高无上的荣誉．

重要的问题历来是推动科学前进的杠杆．但一位科学家如此自觉、如此集中地提出一整批问题，并且如此持久地影响一门学科的发展，在科学史上实属罕见．难怪大数学家外尔(Weyl，1885～1955)在悼念希尔伯特时曾经这样说：希尔伯特就像穿杂色衣服的风笛手，他那甜蜜的笛声诱惑了如此众多的老鼠，跟着他跳进了数学的深河．对于有志于此的人们来说，这23个问题正是这样一种甜蜜的笛声，我们至今似乎仍能听到他的召唤．

值得高兴的是，中国数学家在问题［08］和问题［06］上曾经作出一些贡献．

6.5.2 未来世纪数学问题

希尔伯特所提出的23个数学问题，对20世纪的数学发展影响深远．那么，21世纪应该提出怎样的数学问题呢？而且，现在的数学面广量大.分支既多又细，显然已不是一个人可以驾驭的了．因此，国际数学联盟(IMU)希望由蜚声世界的俄国数学家V·I·阿诺尔德牵头，邀请世界数学家共同解决.希望集中当今主要数学家的智慧，来预测未来数学的发展．

1997年6月，在加拿大多伦多的菲尔兹数学研究所举行庆祝阿诺尔德60寿辰的学术讨论会，斯梅尔在会上作了《未来世纪数学问题》的报告.作为对阿诺尔德邀请函的答复.斯梅尔的讲稿在《数学信使》(Mathematics Intelligencer)1998年第2期上发表．其中提出了18个未来世纪的重大的数学问题：

(1)黎曼猜想；

(2)庞加莱猜想；

(3)P=NP问题；

(4)多项式的整数零点；

(5)丢番图曲线高度的界；

(6)天体力学可以相对平衡态数目的有限性；

(7)二维球面上点的分布；

(8)把动力学引进经济学理论中；

(9)线性规划的多项式时间计算问题；

(10)流形上可微逼近封闭定理；

(11)一维动力学通常是双曲线吗；

(12)微分同胚的“中心化子”；

(13)希尔伯特的问题［16］；

(14)洛伦兹吸引子；

(15)雅可比猜想；

(16)纳维—斯托克斯方程；

(17)解多项式方程组；

(18)人工智能是否有极限．

斯梅尔在选择这18个问题时的原则是：1.陈述简单；2.斯梅尔本人比较熟悉；3.问题十分重要．

2000年5月，美国CLAY数学促进会(CMI)在巴黎法兰西学院举行特别活动，悬赏解决7个数学问题，每个问题100万美元.这7个问题是：

黎曼猜想，庞加莱猜想，Hodge猜想，Birch猜想，P=NP吗？Navier-Stokes(纳维—斯托克斯)方程组，杨振宁—赖斯理论．