如何证明积分函数连续的方法

§4.3　定积分的性质

定积分的性质主要包括以下几类：四则运算；中值定理；逼近性质；积分的连续性；可加性；变限积分求导法，微积分学基本定理；跟定积分有关的极限等等，兹介绍如下：

一、积分中值定理

1．积分第一中值定理

设f（x）在［a，b］连续，g（x）在［a，b］可积且不变号，则存在一点ξ∈［a，b］，使得

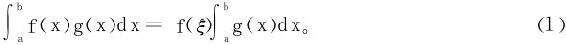
特例：g（x）≡1时。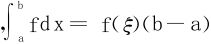

（1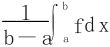）叫做f在［a，b］上的积分平均值。

2．积分第二中值定理

若在［a，b］上f（x）单调，g（x）可积，则∃ξ∈［a，b］，使得

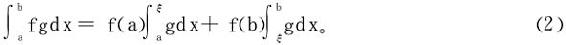
特例1　若f（x）在［a，b］上非负递减且f（b）≥0，则；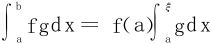

　　2　若f（x）在［a，b］上非负递增且f（a）≥0，则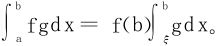

二、积分连续性

若函数f（x）在［A，B］可积，则有

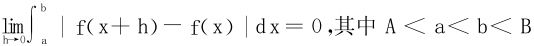
三、微积分学基本定理

f（x）∈C［a，b］，F（x）是f（x）的原函数，则

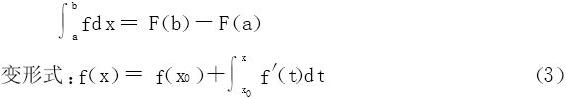
四、可积函数的逼近

设f是［a，b］上的R－可积函数，在L¹空间范数之下，有以下三种不同的逼近方式：

1．阶梯函数逼近

∀ε>0，∃阶梯函数s（x），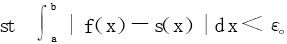

2．连续函数逼近

∀ε>0，∃连续函数g（x），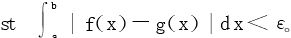

3．多项式逼近

∀ε>0，∃多项式p（x），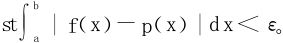

证明思路：

1°利用达布上和、下和及可积第二充要条件。

2°先对阶梯函数证明可以用连续函数逼近。

对于最简单的阶梯函数如设［α，β］⊂［a，b］，

只需作线性连接即可以了，对一般的阶梯函数，类似推广即得。结合已证的1°就得出一般的可积函数可以用连续函数逼近。

3°注意到闭区间［a，b］上的连续函数可以用多项式一致逼近（Weierstrass逼近定理），立即得知。

五、跟定积分有关的极限

关于这一内容最初的介绍可参见§1.2的第二段。在此我们将介绍一些更深刻的结果。设f（x）在［a，b］上R－可积，将［a，b］等分并取端点作为介点。

引入记号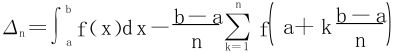表示定积分与黎曼和数的差，则有Δ_n→0（n→＋∞），若对f（x）再加上一些条件，就可得到以下深刻的结果。

1．设f（x）在［a，b］上可导，且f′（x）在［a，b］上可积，则

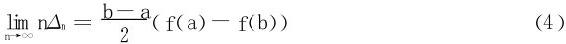
证明　由f′的可积性，于是达布上和、达布下和有相同极限证之。

记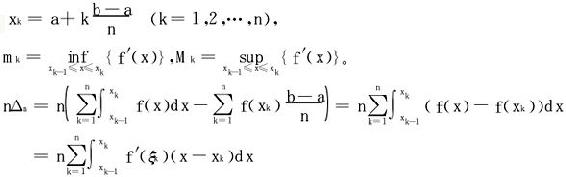

式中ξ_k∈（x_k－1，x_k）由拉格朗日中值定理得出。

因m_k≤f′（ξ_k）≤M_k，

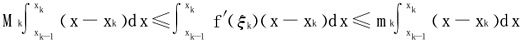
即

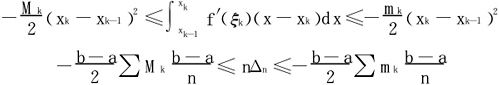
令n→∞得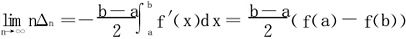

2．记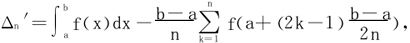

则当f″∈R［a，b］时，有

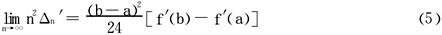
证明从略，可参阅［11］P148－150。

例1　求出正值连续函数f>0，使得

解　从条件知f²（x）可导，又由f（x）>0，且f连续

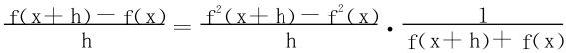
得出f（x）亦可导，（6）式两边关于x求导，得出，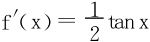

故。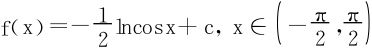

令x＝0，知c＝f（0）＝1，所以。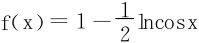

例2　设f（x）∈C［a，b］，若下述三个条件之任一个成立，证明f（x）≡0。

1. ∀φ（x）∈C［a，b］，有；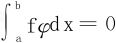

2. ∀φ（x）∈C［a，b］，且φ（a）＝φ（b）＝0，有；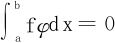

3. ∀n＝0，1，2，…，有。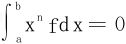

证明　1．只要取φ（x）＝f（x）。

2．反证法，若∃x₀∈［a，b］，st　f（x₀）≠0，不妨设x₀∈（a，b），由连续函数的性质（极限保号性），存在x₀的一个δ－邻域U（x₀，δ），使得在其上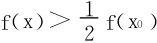恒成立，构造φ（x）为折线函数；

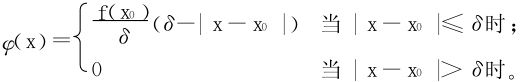3．利用连续函数的多项式一致逼近，存在多项式序列｛p_n（x）｝，在［a，b］上p_n（x）⇒f（x），立得。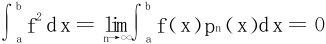

例3　设f（x）在［a，b］可积，试证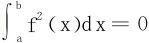的充要条件为f在连续点上为0。

证明　必要性：反证法易证。

　　　充分性：

法一　用实变函数知识去证明，由可积的第四充要条件，f（x）的不连续点E的测度为0，而在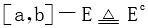上，f（x）恒为0，故

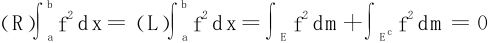
法二　设法证明f（x）的连续点处处稠密，即证∀［α，β］⊂［a，b］，f在［α，β］上必有连续点。当取连续点作为介点时，黎曼和数恒为0，故得知。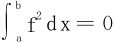

等价转化：证明可积函数f（x）在［a，b］内至少有一个连续点。下面分析函数f（x）在某一点x₀处连续的振幅特征。

以w_δ（f）表示f在（x₀－δ，x₀＋δ）上的振幅，即

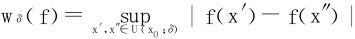
则有如下刻划f（x）点态连续性的结论。

引理　f（x）在x₀连续。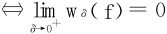

引理的证明从略。下面继续充分性的证明。依据f（x）的可积性，∀ε>0，∃分法T，st∑w_iΔx_i<ε

由抽屉原则，至少有一个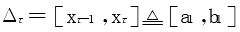，在其上，振幅w_τ<ε／（b－a）；再由f在［a₁，b₁］上可积，可有［a₂，b₂］⊂［a₁，b₁］，f在［a₂，b₂］上的振幅充分地小。

先取ε＝b－a，存在某个Δτ，在其上w_τ（f）<1，再在［x_τ－1，x_τ］上取一个子区间［a₁，b₁］，使得b₁－a₁<1，自然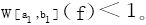

由于f在［a₁，b₁］上仍可积，继续上述步骤，可选出［a₂，b₂］⊂［a₁，b₁］，使得

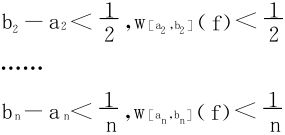
由区间套定理，存在唯一c∈［a_n，b_n］，于是依据上述引理知f（x）必在c点连续。

例4　设f∈C［a，b］，若∀φ∈C［a，b］，同时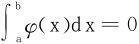的φ（x），有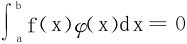。证明f（x）恒为常数。

证明　若f（x）已经满足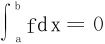，则特取φ即为f可得。

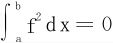若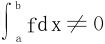，构造新函数，

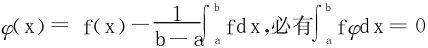又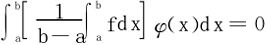　

得出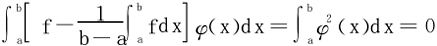　

所以φ（x）≡0，即。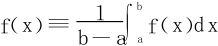

例5　设f∈C［a，b］，且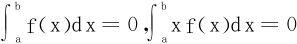，证明至少存在两点x₁，x₂∈［a，b］，使得f（x₁）＝f（x₂）＝0。

证明　显见至少有一个零点。反证，若恰有一个零点x₁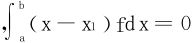，但（x－x₁）f（x）在［a，b］－｛x₁｝上保号，从而积分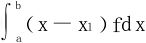必为正值或负值。矛盾。

推广：设f∈C［a，b］，∀n≤N，有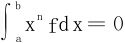，试证f（x）在［a，b］上至少有N＋1个互异的零点。

（分析：N＝2时，先证明，引入g（x）＝（x－x₁）（x－x₂），f，g除去x₁，x₂之外保号，…）

思考：若∀n＝1，2，…皆有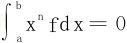，则f≡0（不仅是有可数多个零点而已啦）。

例6　设f∈C［0，1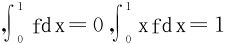］，证明∃x₀∈［0，1］，使得｜f（x₀）｜≥4。

证明　反证法，若∀x∈［0，1］，｜f（x）｜<4，于是

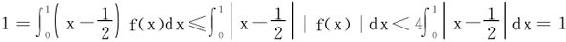
得出矛盾。

推广：条件改为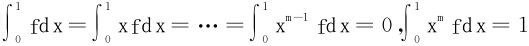，则

∃x₀∈［0，1］，st｜f（x₀）｜≥2^m（m＋1）。

证明　仍用反证法

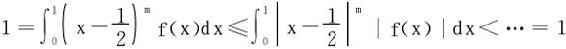
例7　设f（x）∈C（R），T>0，试证f是以T为周期的函数的充分必要条件是积分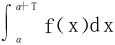的值∀α恒为常数。

证明　必要性易证。

充分性：令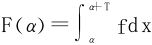，则F（α）≡C，F′（α）＝0

所以f（α＋T）－f（α）＝0，∀α∈R成立，即知f（x）为周期函数。

例8　设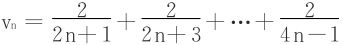

求。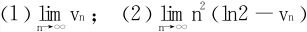

解　（1）对［0，1］n等分，分点为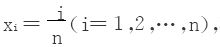在每个小段上取ξ_i为中点，得到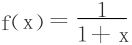的黎曼和数是

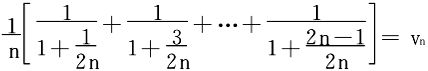
于是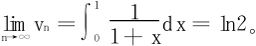

（2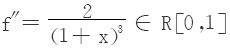），Δ_n′＝ln2－v_n，于是由本节（5）式知

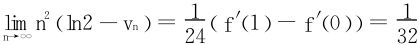
习题4.3

1．设f∈C［a，b］且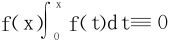，证明f（x）≡0。

2．设f∈C［a，b］且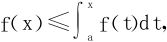则f（x）≤0。

3．设f∈C（R^＋），∀α>0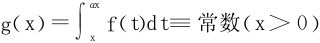，，证明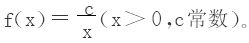

4．设f（x）是连续的周期函数，周期为p，证明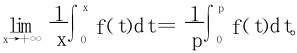

5．设f（x）在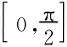连续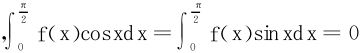，证明：f（x）在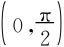内至少有两个零点。

6．设函数f（x）在［0，π］上连续，且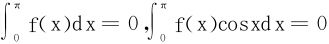。试证明：在（0，π）内至少存在两个不同的点ξ₁、ξ₂，使得f（ξ₁）＝f（ξ₂）＝0。

（2000年数学（三）、（四））

7．设在［－1，1］上连续的函数f（x）满足如下条件：对［－1，1］上任意的偶连续函数g（x），积分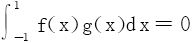。试证：f（x）是［－1，1］上奇函数。

　（证：取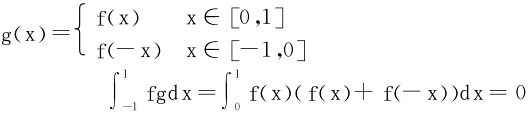

　再取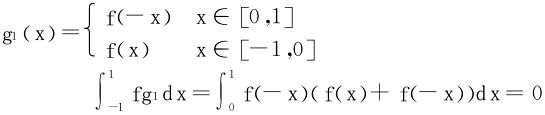

　所以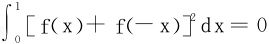，得出∀x∈［0，1］有f（x）＋f（－x）＝0，此证得f（x）为［－1，1］上的奇函数。

　或证　取g（x）＝f（x）＋f（－x）即可以了。

8．设。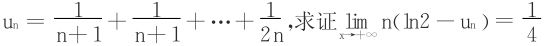

9．设f在［0，1］上可微，且∃M>0 st｜f′（x）｜≤M。求证。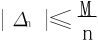

10．设f在［1，＋∞）上连续、递减、恒正，令

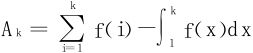
　证明｛A_k｝收敛。

11．设函数f在［0，a］上严格递增，且有连续导数，f（0）＝0。又g是f的反函数。求证∀x∈［0，a］，有。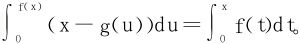

（华东师大2002年）

12．设f在［－1，1］上二阶导数连续，证明∃ξ∈（－1，1），。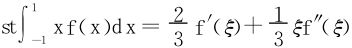

（浙江省高等数学竞赛2005年）