尺寸链在一个零件或部件中,是决定各个表面(或轴线)的相对位置的一组尺寸,此组尺寸按一定顺序排列,且具封闭形式。
零件尺寸链 若尺寸链中所有尺寸都在同一零件上,如图7-16,这样的尺寸链称零件尺寸链(A3=A1-A2)。
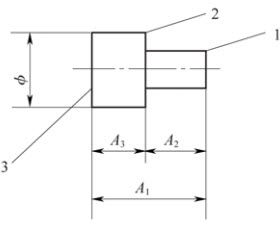
图7-16 零件图(1、2、3为平面)
装配尺寸链 若尺寸链的尺寸不在同一零件上,如图7-17,这样的尺寸链称装配尺寸链(A3=A1-A2)。

图7-17 装配图(1、2、3为零件)
环——组成尺寸链的各个尺寸简称“环”。
组成环——组成尺寸链的基本尺寸,如图7-17中之A1、A2,叫做组成环。
封闭环——在零件加工完成时,或在部件装配完成时,才形成的尺寸,叫做“封闭环”,如图7-17中的A3。
组成环由增环和减环组成。
增环——某组成环增大,其他组成环不变,若封闭环随之增大,则称此环为增环。例如图7-17中A1。
减环——某组成环增大,其它组成环不变,若封闭环随之减小,则称此环为减环。例如图7-17中A2。
第一步,“找环”——正确找出尺寸链各环。
根据尺寸链主要特性判断:
(1)每一尺寸链的各环排列成封闭的形式,不封闭的不是尺寸链。
(2)尺寸链中任一组成环大小的变化将引起封闭环大小的变化,不引起封闭环大小变化的尺寸,不是本尺寸链的组成环。
(3)一个尺寸链中,只有一个封闭环,最简单的尺寸链是三环尺寸链。
第二步,“区分”——分清同一尺寸链中,哪些是封闭环,哪些是组成环,哪些是增环,哪些是减环(可与第一步并行)。
第三步,画出尺寸链图。作图可从任一表面或轴线开始,依次画出所有环,包括封闭环。各环不必按比例,可用向量表示。将增环定为向上,减环向下,封闭环方向与减环一致。链图应封闭。各组成环公称尺寸和上下偏差在链图上注明。
计算方法:
若增环之和为 ,减环之和为
,减环之和为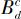 ,
,
则封闭环:
式中 A——增环各公称尺寸之和;
a——增环各公称尺寸上偏差之和;
b——增环各公称尺寸下偏差之和;
B——减环各公称尺寸之和;
c——减环各公称尺寸上偏差之和;
d——减环各公称尺寸下偏差之和;
(A-B)——封闭环X的公称尺寸;
a-d——X的上偏差;
b-c——X的下偏差。
例1 某轴尺寸如图7-16所示。若A1=16+0.2,A2=9+0.1,求A3。
解:
例2 某轴尺寸如图7-17所示。若A1=18+0.1,A2=16-0.1,求A3。
解:
例3 某轴尺寸如图7-18所示。求X值及上下偏差。

图7-18 某轴尺寸图
解:画尺寸链图:
求X值的计算简图:
求得:

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















