研究自然的定量方法

我们可以说，现在首次打开了通往崭新方法的大门；在未来的岁月里，这一拥有无数美妙神奇结果的新方法将赢得更多心灵的重视。

伽利略（Galileo）

一天，一位在比萨（Pisa）大学就读的青年学生，去参观著名的比萨城大教堂。礼拜仪式令人感到十分乏味，使人生厌，因此他没有认真听牧师的布道讲演，而是注视着一盏悬挂着的来回摆动的大吊灯。他很快就注意到，当吊灯摆动经过一段大弧时，它完成这一摆动所花的时间，似乎与它经过一段小弧所花的时间一样多。他没有伸手从口袋中掏出表来核实这一观察结果，原因很简单，当时还没有发明这种计时器呢；但是，他的确想到了利用自己脉搏的跳动来核实自己的判断。这一观察结论被证明是正确的。这样，这位很年轻的学生，已经发现了一条支配所有摆运动的科学定律：一个单摆完成一次摆动所需的时间，与摆的振幅无关。不久，这条定律就被用于设计当时这位年轻人正需要的、具有广泛用途的钟表。更为重要的是，这一发现揭示出了科学活动中的一个新观念，这一观念勾画出了近现代科学的特色，同时也使得科学具有了“神奇的”力量。下面，我们就要准备考查这一观念。

这位在教堂里遐想的年轻人，就是G·伽利略（Galileo Galilei），一位音乐家的儿子，于1564年即莎士比亚出生的那年，出生于佛罗伦萨（Florence）。17岁那年进入比萨大学学医，而这时，他却私下师从一位富有实践经验的工程师学习数学。通过阅读欧几里得和阿基米德的著作，唤起了他在数学和科学方面的天赋才智。征得父亲的同意后，伽利略将自己的注意力转向了数学和科学。

伽利略的兴趣和活动范围，即使是对于一个天才时代的伟大智者来说，也是难以置信的广泛。他始终对机械仪器有着浓厚的兴趣，而且在这方面心灵手巧。在家里，他拥有一间实验室，在此度过了大量的时间。伽利略制作了大量新奇、非常灵巧又用途极大的仪器，因此人们称赞他是现代发明之父。望远镜——被桂冠诗人本·琼森（Ben Jonson）称之为“迷惑镜”——就是由伽利略发明的。他利用自己发明的望远镜发现了木星和土星的卫星、银河系恒星的组成、金星的盈亏，以及月球上的环形山。这些观察的结果，明显地表明了天体具有与地球同样的性质飞从而为日心学说提供了十分有力的证据。伽利略的另一个发明是听诊器，利用他自己发现的单摆运动规律，他发明了这一仪器，并将它用来纪录脉搏跳动的频率。

尽管他的科学研究业绩的光辉遮盖了其他活动，但值得指出的是他还是一位文学大师。人们认为，他写出了17世纪最优美的意大利文散文。他曾用各种文学形式进行诗歌创作，发表评论文章，而且还曾一度讲授过有关诗人但丁的专题课。甚至他的科学著作之所以著名，也不仅仅因为这些著作介绍了他在天文、物理方面的研究成果，而且因为它们同时也是文学经典名著。伽利略在文学艺术方面的兴趣，导致了对绘画的酷爱和娴熟的音乐才能，在他遭受痛苦的岁月里，绘画、音乐给他带来了安慰。

雄心勃勃的伽利略最富有艺术性、最富有成果的创造，是他阅读大自然这部书的宏大规划。在本质上，这个规划提出了关于科学目标的一整套新观念，以及在实现科学研究目标的过程中数学所起的作用。尽管人们早些时候在这方面不够广泛又不够成熟的努力应该得到承认，但是伽利略清晰地构造出了这一规划，并且通过建立一些基本定律将其付诸实际应用。伽利略誉满寿高，当他于1642年去世时，他已经获得了巨大的声誉。从那时起，现代科学已经信心十足地在他那极富成果的道路上起程了，这一成就必须归功于伽利略几乎是单枪匹马的奋斗。我们在这一章所着力讨论的，正是伽利略研究和把握大自然的规划。

毫无疑问，几乎每一个20世纪的人都意识到，大约在1600年，在科学中发生了革命性的变化。为什么在17世纪开始的科学活动会被证明具有如此大的作用呢？是否笛卡儿、伽利略、牛顿、惠更斯、莱布尼茨这些献身科学的勇士们，比早期文明中的勇士们更聪明呢？未必！思想深刻、博学多才的亚里士多德和卓越的阿基米德，都具有17世纪任何一位科学家所具有的那样杰出的才智。是不是因为增加使用了由罗吉尔·培根和弗兰西斯·培根所提出的观察、实验和归纳的方法呢？显然不是。求助于观察法和实验法，可能是文艺复兴的一大发明，但作为一种研究方法，至少希腊科学家对此也很熟悉。把近代科学巨大的、令人惊奇的成果，仅仅解释为是在科学研究中利用了数学，这也不对。因为尽管17世纪的科学家们知道，他们工作的目标，是为了找出隐藏在各种现象后面的数学关系，但对自然界的这种关系的寻求在科学中并不是什么新东西。自然界具有数学设计的观点，甚至在希腊时代就已经受过考验了。

近代科学成功的秘密，就在于在科学活动中选择了一个新的目标。这个由伽利略提出的、并为他的后继者们继续追求的新的目标，就是寻求对科学现象进行独立于任何物理解释的定量的描述。如果把近代科学与以前的科学活动进行比较，那么我们将会更加懂得科学中这一新观念的革命意义。

希腊科学家们主要致力于解释现象为什么会发生的原因。例如，亚里士多德花费了大量时间，试图解释为什么扔向空中的物体会落到地球上。希腊数学家和工程师海伦，利用自然界厌恶真空的原理去解释其他现象。同样地，希腊物理学家对没有明显的力引起天体作圆周运动这一问题所作的说明是：圆周运动是自然的运动，因此就不必需要产生或保持这种运动的力。其他的“解释”似乎也不能清楚地阐释他们所研究的现象。例如，按照柏拉图的说法，地球在宇宙的中心保持着自己的固定位置，是因为处于恒定不变的本体中平衡的物体，无需担心它会向某一方向作或多或少的偏离。

中世纪欧洲同样也关心事情为什么会发生的原因，只不过总是按照现象的目的来作解释罢了。为什么下雨的“解释”，就是在于雨浇灌人类的庄稼。庄稼成熟后给人以食物，而人活着则是为了服务于上帝，崇敬上帝。圣·托马斯（St Thomas），继承亚里士多德的思路，从事物为什么发生的观点讨论运动，说之所以产生运动就在于，物体自身有一种企图实现自己运动的潜能。无论这些解释是否能令我们满意，这些的确是早期科学活动中对所提出的问题给出的答案。

伽利略第一个认识到，这些关于事件原因和结果的玄想，远远不能增进科学知识，丝毫不能给人们以任何揭示和控制自然界运动的力量。有鉴于此，他提出要以一种关于现象的定量描述来取代那些玄想。

我们通过一个例子来说明他的想法。一个球从某人手中掉下，对于这一简单的情形，我们可以没完没了地猜想球为什么落下的原因。但伽利略却建议我们另辟蹊径。球从起点下落的距离，随着从它落下的那一瞬间开始所经历的时间而增加。因为球下落的距离和它下落所经历的时间，这两者都是变化的，所以用数学语言来说，这两者都称之为变量。伽利略提议，让我们来看看这些变量间的数学关系。伽利略所给出的答案，用今天的科学表示法写出来，就是众所周知的公式；对于刚才所讨论的情形，这个公式就是d＝16t²。这个公式表明，球在t秒内所下落的英尺数，是这一时间的平方的16倍。例如，在3秒钟内，球下落16乘以3²即144英尺；在4秒钟内，球下落16乘以4²即256英尺，等等。

首先，应注意到，这个公式是严密、精确、完全定量的。对于一个变量的每一个值，在这种情形中的时间，以及对应的另一个值距离，都能进行精确的计算。这可以对成百万次的时间变量值进行计算，实际上可以对无穷多个值进行演算，所以这个简单的公式d＝16t²包含有无穷多种情况。

公式是表示变量间某种关系的一种方法。物理现象中存在的已知关系式本身，在今天被称之为一个函数或函数关系。这样的关系在每一种实际情形中都存在。由于大气压随地球表面上空的高度而变化，所以在气压和高度之间有一种函数关系。类似的，一件生产出来的商品的价格，依赖于原材料价格、劳动力价格和行政管理费用，也就是说是它们的一个函数。在最后一种情形中，牵涉到4个变量，其中的一个，即商品的价格，依赖于其他3个。

数学公式是对于所发生事件的一种描述，而不是对引起这种事件因果关系的一种解释，认识到这一点非常重要。公式d＝16t²，对于球为什么下落，以及球在过去或将来是否继续下落等问题没作任何说明。它仅仅给出了关于一个球如何落下的定量描述。尽管这样的公式被用于描述科学家所发现的因果相关的变量，但科学家无须研究或理解这些因果关系，也能成功地处理变量间的数量关系。正是如此，伽利略已经清楚地看到，当他强调数学描述时，就是反对把很少获得成功的定性研究和因果研究纳入自然界。

然后，伽利略决心寻求描述自然行为的数学公式，这种思想，像大多数天才思想一样，当第一次接触到时，可能不会给读者以太深的印象。在这些单纯的数学公式中，似乎没有什么真正的价值。它们解释不了什么东西。只是以一种精确的语言来对事情作描述。但是，这些公式却被证明是人类所获得的关于自然界最有价值的知识。我们将发现，近代科学在实用方面和理论方面最激动人心的成就，主要是通过熟练地运用日积月累的定量的、描述的知识才获得的，而不是通过关于现象原因的形而上学的、神学的甚至是机械论的解释。近代科学的历史，就是逐渐摒弃上帝和恶魔，从而将关于光、声、力、化学过程以及其他概念的模糊思想转变为数量关系的历史。

寻找描述现象的公式的规划和决策，紧接着又引出了这样的问题：公式中应该涉及什么量？一个公式涉及整个物理变化中大量的数值，如压力、温度。因此，这些性质应该可测量。伽利略接下来所要遵循的下一个原理，是划分哪些是可测量的量，哪些是不可测量的量。这样，他所研究的问题就转变为，使关于自然现象的诸方面，基本性质的内容与能够被测量的内容彼此分开。

为了实现这个目标，伽利略必须开辟新的道路。中世纪的先辈们——那些亚里士多德的追随者们，利用一些诸如像起源、本质、形式、性质、因果性、目的之类的概念研究自然界。但这些范畴本身并不能定量化。因此，伽利略必须着手利用由他自己和笛卡儿共同创立的自然哲学。笛卡儿已经把物体在空间和时间中的运动，当作是一条固定的自然界基本现象。一切活动都可以利用这些运动的机械现象予以解释。事实上，物质本身是原子的集合体，原子的运动不仅确立了该物体的行为，而且也确定了由该物体所产生的感觉。

因此，伽利略着手将运动中能够测量的物质的特性分离出来，然后将它们与数学定律联系上。通过分析和思考自然现象，他决定将注意力集中在这样一些概念上，如空间、时间、重量、速度、加速度、惯性、力和动量。后来的科学家又补充了能、能量和其他概念。在这些特殊的性质和概念的选择中，伽利略再度显示出了其天才，因为他选择的概念并非一眼就能看出其重要性，而且也不是很容易被测量。有些概念如惯性，甚至并不明显地为物质所具有；他们的存在必须从观察中才能推断出。其他一些概念如动量，则必须归功于他的独创。这些概念在征服自然界、使自然界理性化的过程中，的确被证明具有伟大的意义。

在伽利略研究科学的方法中，还有另一个基本要素，后来这一要素被证明也十分重要。应该为科学建立数学模型。伽利略和他忠实的信徒们相信，他们肯定能找出物理世界的一些定律，这些定律将无可置疑地必定是真理，就如同欧几里得的经过任意两点只能画出一条直线的公理一样。也许冥思苦想、实验或观察也能揭示出这些物理学公理；至少它们一旦被发现，那么它们的真理性凭直觉就可断定为真。利用这些十分重要的直觉，17世纪的科学家们希望能推导出大量其他精确的真理，就如同从欧氏几何的公理中推导出定理一样。

为了正确评价伽利略规划的重大意义，我们必须认识到，科学并不是一系列实验，无论这些实验做得多么巧妙，怎么有水平；同样，科学也不是一系列由实验或理论推导出来的事实。一门科学的真正内容，就是一个理论体系，这个体系以首尾连贯一致的形式包含、组织、叙述、阐明一系列看起来似乎互不相关的事实，而且这个理论体系能够推导出关于物理世界的新结论。单个的事实或实验本身几乎没有价值。价值就在于把它们联系起来的理论。从太阳到行星的距离是些枝节问题，日心学说理论则是第一个庞大的知识体系。所以伽利略的另一个重大变革，就是使科学理论将大量的事实联系在一起，从而形成了能从一系列公理中进行演绎的数学定律体系。

因此，伽利略的规划包含3个主要的特征。第一，找出物理现象的定量描述，并使它们能包含在数学公式中；第二，分离出并且测量最基本的现象的性质，这些在公式中就是变量；第三，在基本的物理原理基础上，建立起演绎科学。

为了使这个规划得以实施，伽利略必须找出基本定律。我们可以得到泰国的结婚数目逐年变化的数学公式关系，或者纽约城马蹄铁价格逐年变化的数学公式。但是，这样的公式在科学中没有什么价值，因为它没有包含——无论是直接还是间接——任何有用的知识。研究基本定律是另一项巨大的任务，因为伽利略必须再一次打破陈规。在关于物体运动的研究中，他的方法就必须要考虑到地球在空间中的运动，以及地球的自转运动，这些事实本身就足以使文艺复兴时期世界所有庞大的力学体系——亚里士多德体系失去效力。

在讨论地球上物体的运动时，亚里士多德这位古希腊圣人教导说，每一个物体都有一个自然位置，物体的自然状态就是处于静止中的自然位置。重物体的自然位置位于地球的中心，当然它就是宇宙的中心。轻物体，如气体，它们的自然位置则在天空。对于不在自然位置的物体，在没有其他外力作用的情况下，将趋向自然位置。这样就产生了自然运动。例如，从手中落下的一个物体将趋向地球中心并且向地球中心运动。但当上抛或提起一个物体时，产生的运动则偏离自然状态。

既然静止是自然状态，那么自然运动和偏离运动都必须归结为某种力的连续作用，否则运动将会停止。所有的运动也都会受到连续不断的阻力，在任何情况下，运动的速度都能由公式（利用现代符号标记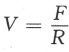）表示；用语言来表述，即：速度与力成正比而与阻力成反比。在自然运动状态，力就是物体的重力，阻力则来自物体运动中的媒介质。因此在同一种给定的媒介质中，较重的物体必然下落得较快，因为在公式中，F较大，所以V也必定较大。在偏离自然状态的运动中，力由人的手或某种人造机器施加，而阻力则来源于重量。这样，较轻的物体则阻力R较小，所以速度V就较大。因此，当施加一给定的力时，较轻的物体运动得较快。

解释某种特殊的现象，需要特殊的理论。例如，下落的物体，速度总是很快。在这种自然运动中，由于力由重力提供，那么这个力的值就与介质中的阻力一样，是个常数。因此，由公式，速度也应该是个常数。加速度，即速度的增加量，通过物体从前一个位置到后一个位置的空气推力可以计算出。这样，空气就被设想为在物体后面施加了一个力，从而使物质加快了速度。没有什么科学思想的人竟然解释说，正像一个思亲心情急迫的人返回故里一样，物质越临近自然状态即快到家（地心）时，其速度就愈快了。

亚里士多德的上述定律，系由二份观察加上八份美学、哲学原理得到。但是，在许多世纪里，这些却被当作宗教、哲学和科学著作的金科玉律般的基础。我们可以肯定，伽利略揭示自然界的基本规律，就像哥白尼提出日心学说一样，阻力极大。因为他必须打破2000多年来根深蒂固的传统思想。

按照亚里士多德的理论，使一个物体保持运动就需要一个力。因此为了使一辆汽车或一个球，哪怕是在非常光滑的地面上运动，也应该给予一个力。但是，伽利略对这个现象的观察，却比亚里士多德深刻得多。事实上，一个滚动的球或运动的汽车，只受空气的轻微阻碍和受它们与运动表面之间的摩擦力的阻碍。如果这一类的阻碍不存在的话，那么维持自然运动就不必需要推动力了。它将继续无限地保持相同的速度；而且，沿一条直线运动。这条基本运动规律，一个不受外力作用的物体，将无限地以匀速继续在一条直线上运动，是由伽利略发现的，现在就是众所周知的牛顿第一运动定律。明显地，对同一种情况，伽利略所发现的这条定律，比亚里士多德的理论所揭示的要深刻得多。这条定律表明，一个物体只有受到一个力的作用时，才会改变其速度。这样，物体具有抵抗速度变化的特性。物质的这种特性，即抵抗速度变化的性质，称之为物体的惯性质量，或简称为质量。

在我们进一步讨论伽利略的思想之前，应该指出的是，正是他的第一条原理就与亚里士多德的理论相矛盾。这是否意味着亚里士多德犯了明显的错误，或者是他所做的观察太粗浅或太少了，因而不能得出正确的原理呢？完全不是这样！仅仅依靠观察，几乎不可能使亚里士多德改进自己的理论，或启发其他人改进他的学说。亚里士多德是一位持有现实主义观点的大学者，而且他一再教导说，要通过实际观察后再做出结论。但是，伽利略的方法更加精细，更有可能获得成功。伽利略研究问题时是作为一位数学家。通过忽略一些因素而突出其他事实，这样就将现象理想化了，就如同数学家们通过除去某些东西，突出个别性质而将绷紧的线和直尺的边缘理想化一样。通过忽略摩擦力和空气阻力，而且想像物体是在一纯欧氏空间中运动伽利略就发现了这条正确的基本原理。他的技巧是，将问题用几何方法进行处理，然后再得出定律。

但是，我们会问，没有摩擦力和空气阻力是真实情况吗？难道它们不会使得物体速度减少，最后完全停止吗？有时会这样；而且当这种情况发生时，应该考虑摩擦力和空气阻力。但是，它们是附加在基本现象中的作用，不会影响结论，也就是说，一个物体的运动将继续无限地以匀速进行。有时，摩擦力和空气阻力实际上也可以忽略不计，如当一个一磅重的铅片从100英尺的高空落向地面时。同时也要认识到这样的事实，这些附加力的存在也有可能减少它们的作用，油、滚珠轴承和光滑表面，就能减少机械运动时的摩擦。而当这种效应不能减少时，就应该承认它的存在，从而使我们能明确地进行考虑，选择正确的运动方式。伽利略在这里的观点，是标准的数学家处理理想图形的观点。真实地测量三角形时，量得的内角角度之和也许在160°到200°之间变化。基本的事实是，一个理想三角形的内角之和是180°，因此，只要一个三角形近似地是理想三角形，则它的内角之和将近似地为180°。现代科学成就产生的一个悖论是，科学家或者数学卜家通过理想化，似乎故意使一个问题变得面目全非，以致使他有意采取与一般观点不同的方法，然而他们在后来竟能使问题获得正确的解决。伽利略的这一套方法被证明极其成功和有效，这一点我们马上将会看到。

一个运动着的物体，如果给它施加一个力，将会出现什么样的情况呢？在这里，伽利略做出了第二个重要的发现。连续不断地施加一个力，将会使物体的速度增加或减少。我们称单位时间内增加或减少的速度为物体的加速度。这样，如果一个物体以每秒钟增加每秒30英尺的速度，那么它的加速度就是30英尺每二次方秒，或者采用缩写的形式为（30英尺／秒²）。第二运动定律所描述的是：如果一个力使得一个物体的速度增加或减少，那么用适当的单位来表示，这个力就等于物体的质量与它的加速度的乘积，这个定律用一个公式表示就是

F＝ma　　　　　　　（1）

这个公式具有非常重要的意义。它表明，一个不变的力，在一个质量不变的物体上将产生一个不变的加速度，因为如果F和m都是常数，则a也必定是常数。例如，恒定的空气阻力，速度的减小也是恒定的，它也可以同样说明一个在光滑表面上滚动或滑动的物体，其速度将会逐渐减少，直到速度为零时为止这一事实的原因。

反过来，如果一个运动物体的确具有加速度，也就是如果公式（1）中的a不为零，那么力F也不能为零。从一定高度落到地面的物体的确具有加速度。因此必定有某种力作用在这个物体上。这个力必定就是地球的引力。在伽利略时代，这个观念就已经为某些人接受了。但是，伽利略没有在这个观念上花太多的时间去进行思考，他已经开始把精力花在对下落物体进行定量化研究上了。

他发现，如果空气阻力忽略不计，那么所有下落到地球表面的物体都具有相同的加速度，也就是，所有物体都将以32英尺每二次方秒的相同速率获得速度。如果物体落下，也就是说，仅仅是让其从手上下落，那么它的初始速度为零。因此，在第一秒钟终时，其速度则为每秒32英尺；第二秒钟终时其速度为32乘以2即每秒64英尺；等等。在t秒钟终时，其速度为每秒32t英尺；用符号表示为：

v＝32t　　　　　（2）

这个公式准确地告诉了我们下落物体的速度是如何随时间而增加的。该公式也表明，物体下落的时间越长，则所获得的速度就越大。这是一个众所周知的事实，大多数人都观察到过，从高处落下的一个物体击地时的速度，比从低处落下的物体击地时的速度要大。

为了求出一个下落物体在给定时间内所落下的距离，我们不能采用速度乘以时间的方法，这样给出的仅仅是当速度为常数时的正确距离。不过，伽利略证明了，物体在t秒内所下落的距离的正确公式是

d＝16t²　　　　　（3）

d是物体在t秒内所下落的英尺数。例如，在3秒钟内，物体下落16×3²即144英尺。

将公式（3）的两边同除以16，然后再同时取平方根，我们就得到了一个物体下落一段给定距离d时所需要的时间，它由公式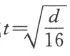给出。应该注意的是，下落物体的质量在该公式中没有出现。这一结论，伽利略通过从比萨斜塔上往下扔物体而进行过检验⁽¹⁾。但是，今天人们依然发现这一点的确难以置信：在真空中从一定高度同时抛下一块铅片和一根羽毛，它们也将同时落到底部。

联系公式（2）和（3），可以推导出另一个有用的公式。在公式（2）的两边同时除以32，我们得到

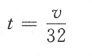
如果将这个t值代入公式（3），我们得到

即

公式（4）告诉我们，如果我们知道了一个自由落体的速度，那么就能计算出它达到这个速度时所下落的距离。

在这个公式的两边同乘以64，就给出

v²＝64d

即

公式（5）给出了一个自由落体下落到距离d时所获得的速度。

现在让我们举一个例子，来看看如何利用运动定律推导出一个重要的公式。我们考虑垂直地向空中抛掷一个球的现象。当然，球离地面的距离（高度）随球上升的时间不断变化。设t是球上抛所用去的时间（秒），从它开始作上抛运动时的瞬间起计时，h是球在t秒内离地面的高度。在这样的情况下，我们将获得关于变量h和变量t的一个有用的关系式。

假设用足够大的力将球抛向空中，使它脱手时的速度达到每秒100英尺。如果没有其他力作用在该球上，那么按照牛顿第一运动定律，球将始终保持这个速度。在t秒内这个球向上运动的距离，等于它的速度乘以它运行所用去的时间。但是，在这个球向上运动的同时，它受到来自地球的吸引力，就像一个作自由落体运动的球一样。按照公式（3），在t秒钟内这个球被吸引向下的距离是16t²英尺。因此，球的运动就是同时发生的两种独立运动的合成，在t秒钟内上升100t英尺，和在相同的t秒钟内下落16t²英尺，因此在t秒钟内球离地面的高度h就是

h＝100t－16t²　　　　　（6）

简单地推导出像（4）、（5）、（6）这样的公式，显示了伽利略如何希望从少数基本的定律出发，实现他推导出自然界重要定律的方案。我们看到，利用物理学原理，数学推理能够演绎地推导出定理。这些例子，以及我们将要考察的其他例子也表明，数学家如何躺在安乐椅中而得到了许多富有重要意义的自然界定律。他的工具，除了纸和笔之外，就是数学公理、定理以及像运动定律这样的物理学原理。数学演绎——这是他的工作的实质——产生了关于物理世界的知识。

从这些证明出发，伽利略又开始进行观察，并且从中获得了另一个运动定律。如果一个物体携带着另一个物体，如飞机装载乘客，则乘客首先应遵从飞机的运动。这似乎毋庸置疑。但是，如果乘客突然从飞机中紧急跳伞，那么他仍将有飞机的水平方向的运动。事实上，如果没有空气阻力和向下的地球吸引力，乘客将完全与飞机一道飞行。这条定律解释了，为什么当地球自转和绕太阳公转时，地球上的物体不会被抛出去的原因。

这条定律对抛物运动的潜在价值非常明显，而且伽利略不久就利用了它。在研究抛物运动时，他注意观察到，一个物体的运动可以归结为两个同时独立的运动。这一发现的意义可以通过一个例子得到证实。一个从一架水平飞行的飞机上扔下的物体具有两种运动。按照刚才所描述的定律，一个是与飞机运行同方向的直线运动，这一运动是由飞机的速度产生的。另一个运动垂直向下。这两种同时存在的运动的合成，就导致物体沿一条曲线向下运动，如伽利略所指出的那样，是抛物线的一部分。但是，下落物体的水平运动和垂直运动彼此独立。如果飞机飞得较快，则该物体的水平运动也将较快，而向下的运动将保持不变。因此，物体将与飞机飞得较慢时落地花相同的时间，尽管在着地以前它在水平方向将飞行得更远。因此，如图48所示，一个物体在O点离开飞机，当飞机速度较大时，它在Q点着地，而飞机速度较小时，它在P点着地，但到达P或Q所需的时间将是一样的。

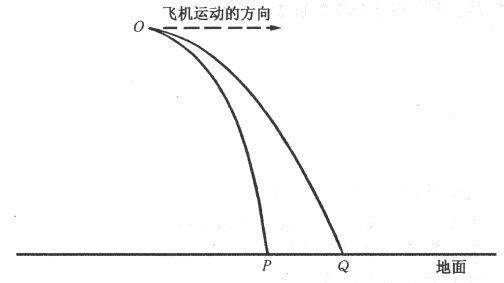
图48　具有不同水平速度的两个自由落体同时着地

伽利略将这个同时独立运动原理应用于炮弹运动的研究，证明了炮弹的运动也是抛物线的一部分，当与地面成45°角发射炮弹时，将得到最大的射程。

所有这些成果和许多其他的成果，伽利略在其《关于两门新科学的方法和数学证明》（Discourses and Mathematical Demonstrations Concerning Two New Science）中给出了详细的阐述，这是一部耗费了他30多年心血的杰作。在这部著作中，伽利略开创了近代物理科学数学化的历程，建立了力学科学，设计和树立了近代科学思维的模式。不幸的是，就在准备出版他的手稿时，伽利略被人以不信仰基督教为由，而禁止出版他的任何著作。这样，他不得不将手稿秘密地转运到荷兰出版，而且还得装着他与印刷出版毫无关系的样子。他强调说，自己的这份手稿不小心在一个偶然的机会中落到了荷兰出版商手里，这位出版商未经他的许可就出版了他的著作。1638年该书出版后，没几年伽利略就逝世了。随着他的去世，意大利思想的独立精神也凋零了。

————————————————————

(1) 即著名的比萨斜塔实验。——译者注