速度和加速度

在研究运动时，有许多标量和矢量具有重要的意义。我们已经探讨过一些标量（温度、距离、时间）和矢量（位移、作用力）。接下来我们将对这些量进行更深入的研究，并介绍一些新的量。

假设一个旅行者能在5小时（hr）的时间内从波士顿旅行350千米（km）到达纽约。已知距离和时间，我们就能定义一个衍生量——平均速率，其算法是用旅行的距离除以旅行的时间。在上面的例子中，平均速率为70千米每小时（70km/hr），由350千米除以5小时求得。70千米每小时大概相当于44英里每小时（mi/hr）。

让我们用v表示“速率”，用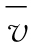表示“平均速率”（在这里，我们用符号上方的横杠来表示该符号的平均值。在后面的章节中横杠又是其他的意思）。我们对某一物体的平均速率的定义是经过的路程（用符号s表示）与所耗时间（用t表示）的比值。于是，用符号表示就是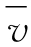=s/t。使用符号不仅方便指称，更有利于我们运用代数方法来处理各种量。不过，在本书中我们很少用到代数。不幸的是，使用符号也是有代价的：我们要么记清楚这些符号代表什么，要么就得在旁边写下它们各自的定义。

要是我们的旅行者在纽约到波士顿的途中不停地看车子的速度计，他就会发现速度计的读数并不总是70千米每小时，而是时高时低。为了弄清楚汽车在任一时间点的速率，我们就需要利用一个概念——瞬时速率。但是瞬时其实不包含任何的时间长度。我们说速率是距离除以时间，但是当时间是0的时候，我们该如何求得速率？我们很小的时候就在数学中学过，任何数都不能除以0。

我们是这样解决这一难题的：将整个距离分为若干小段，然后测量经过每段距离时花费的时间。这样，每段路线上的平均速率即为该段路线的长度除以经过它所耗时长。每段距离越短，相应的耗时便越少。当某段距离和经过它所耗时长短到汽车在这段时间内的变速无法明显地识别时，汽车在这段时间内的平均速率就大约等于汽车穿过这一小段路程的速率。因此，我们可以将物体在某一刻的瞬时速度定义为物体在包含这一时间点的某段无限短的时间内的平均速度。一个更精确的定义是，物体的瞬时速度是当距离和时间取任意长度时，物体平均速度的界限。数学有一个分支用来计算无限小的量，那就是微积分，不过本书不会对微积分进行深入讨论。

就像我们把速率这一标量定义为物体运动的距离与所用时间的比值，我们同样也可以把速度这一矢量定义为物体位移的距离与所用时间的比值。速度这一矢量通常用V表示。速率v是速度的大小。遗憾的是，甚至连物理学家们都会出现用词不考究的情况，错把“速度”当“速率”。正因为这一点，人们经常不得不在上下文中苦苦寻找线索来进行判断。

之前，我们讲到一辆在旅途中变换着速率行驶的小汽车。小汽车在行驶时同样也会改变方向。当一个物体的速率或方向发生变化、或两者都发生变化时，我们称它的速度发生了改变。如果一个物体的速度发生了改变，我们说这个物体经历了加速度（通常用a表示）。跟速度一样，加速度也是一个矢量，尽管加速度的大小——也叫加速率（译者注：英文中没有对加速度和加速率的用词进行区分，两者都是acceleration）——是个标量。因为我们用同一个词表示矢量加速度和标量加速度，我们就得通过上下文进行辨别。不过它们两个的符号却不一样，矢量加速度的符号是a，而标量加速度的符号是a。

我们对加速度的定义是，在某段很短的时间内物体运动速度的变化量与时间的比值，或者说，加速度就是速度的变化率。当小汽车沿着一条笔直的公路加速或减速行驶时，这辆小汽车的加速度实际上只体现在速率的变化上。当小汽车以恒定速度沿着一条曲线行驶时，这辆小汽车的加速度其实是体现在方向的变化上。当然，这辆小汽车也可以边沿着曲线行驶边改变其速率，这也是加速度的表现形式。在日常用语中，降低速度一般称为“减速”，但我们通常用加速这一个词语来代替所有的减速、加速，以及任何情况下方向的改变。

许多人容易混淆速度和加速度的概念，因为两者都是矢量，两者都有各自的方向，且方向还不一定相同。若一个物体的速度和加速度方向相同，这个物体便会沿直线做加速运动。若加速度和速度方向相反，物体则会沿直线做减速运动。若加速度和速度方向形成一个夹角，物体便会沿着一条曲线运动。

当一个物体的速度在某一刻为0时，其加速度有可能不为0。例如，当你向上抛出一个球，当球到达它离地面的最高点时，球的速度便为0。然而，此刻球的加速度不是0，因为尽管球暂时保持静止，它的速度却在发生变化。如果速度和加速度都为0的话，速度就会保持不变，此时球就会在空中一直保持静止不动。这显然与我们的观察不符。

速度和加速度的单位是不同的。因为速度是位移与时间的比值，所以速度的单位是位移的单位，例如米（m）与时间单位——例如秒（m）的比值，如m/s。加速度的单位是速度的单位（如m/s）与时间单位（s）的比值，如m/s/s。这个单位同样也写作m/s2。