不断地累乘

我们都知道国际象棋的发明人向国王求赐麦粒的传奇故事，从而深刻地体会到了一个很小的数字不断用2累乘，其增大速度之快令人震惊，这里再为亲爱的读者讲一些不太熟知的例子。

【题目】1只草履虫经过27小时就会分裂成2只，假设如此分裂出来的草履虫都能存活，那么想使1只草履虫繁衍出的后代所占的体积与太阳的体积相同，需要多久？

提示一：如果每只草履虫分裂出的2只都能活下来，那么1只草履虫的第40代子孙加在一起，可占据1立方米的体积。

提示二：太阳的体积是1027立方米。

【解题】解答本题的关键在于，计算出将1立方米用2乘几次才能得出1027立方米。我们知道：

210≈1000

那么太阳的体积就可以写为：

显然，将1立方米用2累乘90次可以得出1027立方米，这也就意味着，1只草履虫的第40代子孙要再经过90次分裂，或者说，从第一代草履虫开始计算，要经过40+90=130次分裂，其所占体积才会与太阳体积相等。

根据题目可知，1只草履虫经过27小时就会分裂成2只，那么可以计算出，第130次分裂是在第147天。

一位微生物学家曾观察到了1只草履虫的第8061次分裂，这并非杜撰。我希望你能来计算一下，假如这只草履虫的后代全部存活，那么这第8061代会占多大的体积呢？

将思路转回这道题本身，我们觉得还可以把它反过来进行提问：假如把太阳平分成两半，然后再把这两半分别平分成两半，依此类推，那么要分多少次才能使每一个部分的体积都和草履虫一样大？

是的，无论正着问还是反着问，答案都是一样的：130次。但当你意识到把太阳分裂130次就可以使它碎成每一粒只有草履虫大的渣渣时，你还是会觉得过于离奇。

再来提一个与此类似的问题：将一张纸对半撕开，然后把两个半张分别对半撕开，依此类推，要对半分开几次，才能使得到的每一部分纸片都像原子一样大呢？

我们假设每张纸重1克，原子的重量是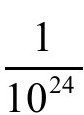克。由于210≈103，所以1024≈280。显然，想把一张纸在不断地对折分开后，使每一块碎片都只有原子的体积那么大，所需要的次数是80次，这与人们所估计的几百万次是截然不同的。