电气系统建模

电气系统的建模过程与机械系统相似，尤其是取消中间变量和化成标准形式运动方程的步骤。

1）理解功能，分析系统，确定输入、输出变量

电气系统中涉及的变量如表2-6所示。

表2-6 电气系统变量

2）采用基本元件画出简化图

表2-7是电气系统涉及的三个基本模型元件即电阻、电容、电感以及两个理想电源元件，即理想电压源和理想电流源。

表2-7 电气系统基本元件

续 表

电阻表征电压与电流的静态特性并发热耗能。电容和电感表征电压或电流变量的动态特性，电容进行电场储能，而电感则进行磁场蓄能，因此电气系统涉及电磁场统一的概念。

这三个元件也可以采用一个统一元件变量即阻抗Z，上述元件均定义为元件输入电压与输出电流的传递函数的同一格式。

无论负载电路如何变化，理想电压源的两端电压恒定不变，理想电流源提供的电流恒定不变。这两个元件都是理想电源元件，实际电源存在内部阻抗，在建模时可以将电源分解为理想电源加实际内部阻抗的形式。

3）推导数学模型

上述基本元件经串联或关联的方式构成实际系统，连接时遵守基尔霍夫定律。基尔霍夫定律分为基于回路的电压定律和基于节点的电流定律。

基尔霍夫电压定律指电路中沿任何封闭回路的总压降为零，即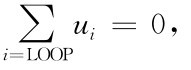具体如图2-16（a）所示，有u1＋u2－u3－u4＝0。

基尔霍夫电流定律指电路中任何一个节点的电流代数和为零，即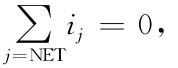图2-16（b）所示，有i1＋i2＋i3＝0。具体如

图2-16 基尔霍夫定律

后续取消中间变量和化成标准形式运动方程与机械运动系统完全一致，不再赘述。

［例2-10］ 对图2-17（a）所示的电气电路建立输入电压u与输出电流i间的传递函数模型。

图2-17 电路

［解1］ 采用霍尔基夫电压定理，标记电压如图2-17（b）所示，并定义电流i1，按基本元件定义可得

uR1＝R1i1

uR2＝R2（i1－i）

uL＝

uC＝C∫idt

对两个回路应用基尔霍夫电压定律可得

u－uR1－uR2＝0

uR2－uL－uC＝0

共7个变量6个方程，拉氏变换并消除中间变量，可得到输入电压u与输出电流i间的传递函数

［解2］ 采用霍尔基夫电流定理，标记电流如图2-17（c）所示，并定义节点A和B，按基本元件定义可得

u－uA＝R1i1

uA＝R2i2

uA－uB＝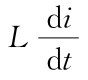

对节点A应用基尔霍夫电流定律可得

uB＝C∫idt

i1＝i2＋i

共6个变量5个方程，拉氏变换并消除中间变量，可得到输入电压u与输出电流i间的传递函数

电气系统建模时结合具体电路器件应考虑负载效应。如图2-18（a）所示的RC电路，假设后继无负载，即电流i1全部流经电容C1可以推得

图2-18（b）中两个相同类型的RC电路串联，第二个RC电路是第一个RC电路的负载，电流i1不再全部流经电容C1，而是分流了电流i2到第二个RC电路。将串联后的电路作整体建模，可以得到

图2-18 电路

但如果两个RC电路间加入一个输入阻抗无限大输出阻抗无限小的隔离放大器，如图2-19 （c）所示，则电流i1不再分流，可对隔离前后的电路分别建模，从而有

隔离放大器常采用运算放大器电路。运算放大器为输入阻抗无限小、输出阻抗无限大的有源器件，图2-19（a）中是其简化原理符号，输入电压u1、u2与输出电压uo间有关系式

图2-19 运放及运放电路

uo＝K（u2－u1）

K为运算放大器增益，K≥1。

在图2-19（b）中标记运放电路的中间变量i1、i2和u1，两个电阻元件分别有

节点u1处运算放大器输入阻抗无限小，有

i1＝i2

K≥1，uo为有限值，则

u1≈0

因此有

整理后得

即此运放电路为反相放大电路，当R1＝R2时则成为反相跟随器uo＝－ui。