精度的基本概念

控制精度是控制系统的基本要求之一，稳态误差是用来衡量控制精度的性能指标。系统的稳态误差由系统结构形式、信号类型、内外扰动和系统元器件性能状况决定。其中元器件性能的精度不高、摩擦、老化、间隙以及零点漂移等缺陷引起的动态系统稳态误差只能通过针对性地改进元件解决。本节将讨论由系统结构类型和输入信号（包括控制作用和扰动作用）形式所引起的原理性稳态误差。

1）精度的定义

精度首先表征为系统的实际工作量的误差，误差有两种定义。一是如图4-11所示的控制系统中将误差定义为输入信号R（s）与反馈信号B（s）之差，即

E（s）＝R（s）－B（s）＝R（s）－C（s）H（s）　（4-1）

图4-11 系统方块图

另一种误差定义是从系统的输出端定义，即误差信号E′（s）是指希望输出量Cr（s）与实际输出量C（s）之差，

E′（s）＝Cr（s）－C（s） 　（4-2）

根据反馈控制系统的工作原理可知，当E（s）＝0时，意味着系统输出量完全复现输入信号，这时被控制的输出量实际值与希望值相等，即Cr（s）＝C（s）。令式（4-1）的E（s）＝0，就得到被控制的输出量希望值

Cr（s）＝R（s）／H（s） 　（4-3）

将式（4-3）代入式（4-2）求得

E′（s）＝R（s）／H（s）－C（s） 　（4-4）

再将式（4-1）写成

E（s）／H（s）＝R（s）／H（s）－C（s） 　（4-5）

比较式（4-4）和式（4-5）可得

E′（s）＝E（s）／H（s） 　（4-6）

式（4-6）就是两种误差间的内在联系。单位反馈系统中H（s）＝1，两者具有相同数值，但量纲可能不同。E（s）易于测量并有一定物理意义，因此通常系统误差分析采用E（s），必要时再由式（4-6）得到E′（s）。

误差e（t）是一个时间函数，当要求给出性能指标时，需要基于e（t）定义精度指标。最基本的定义就是稳态误差

即时间无穷大后误差的情况。

考虑到e（t）是个动态的时间函数，人们构建了一系列包含动态情况的精度指标，在时域中定义有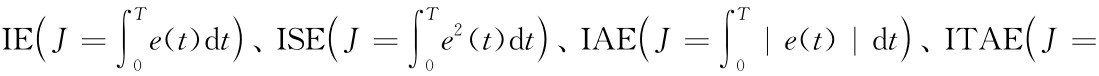等。针对这些定义寻找“最优”，可得出一系列标准式。比较可惜的是上述指标在实践应用（如系统设计、校正）时应用性较差，无法给出系统校正方向，目前尚在应用的是ITAE结合极点配置，表4-2是针对不同输入时不同阶次的ITAE标准式。

表4-2 ITAE标准式

图4-12 系统方块图

2）稳态误差计算

一般控制系统如图4-12所示，R（s）为控制输入信号，对于不同R（s）引起的系统稳态误差ess可用来衡量系统的精度。N（s）为扰动信号也可引起稳态误差esn，特别对于恒值系统，抑制扰动信号的影响是系统主要任务。根据线性系统的叠加原理，系统稳态误差

es＝ess＋esn

（1）系统在控制输入信号作用下的稳态误差。

图4-12所示系统中取G（s）＝G1（s）G2（s），令扰动输入信号N（s）＝0，由输入信号R（s）引起的误差

如果误差信号收敛，根据终值定理可得系统跟随R（s）的稳态误差

由式（4-8）知，稳态误差与系统结构G（s）H（s）和输入信号R（s）的形式有关。

（2）系统在扰动作用下的稳态误差。

图4-12所示系统中若令控制作用R（s）＝0，即可得扰动作用下的误差为

如果误差信号收敛，根据终值定理，该稳态误差esn为

由式（4-10）知，稳态误差与系统结构G（s）H（s）和扰动信号N（s）的形式有关。

需提醒的是式（4-8）、式（4-10）通过误差传递函数并运用终值定理求得，不适用于误差信号不收敛的场合。

［例4-10］ 单位反馈系统的开环传递函数为G（s）H（s）＝，试求：（1）当输入信号为单位阶跃函数r（t）＝1［t］和单位斜坡函数r（t）＝t时，系统的稳态误差ess；（2）若系统的开环传递函数G（s）H（s）保证不变，而反馈通路传递函数由H（s）＝1改为H（s）＝2，求系统希望输出量与实际输出量之差。

［解］ （1）根据式（4-8）可得

单位阶跃函数输入时，R（s）＝1／s，所以

单位斜坡函数输入时，R（s）＝1／s2，有

（2）根据式（4-6）得E′（s）＝E（s）／H（s）＝E（s）／2，对此式进行拉氏反变换得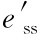，＝ess／2。

单位阶跃输入时，希望输出量与实际输出量之差为e′ss＝0．05／2＝0．025；

单位斜坡输入时，希望输出量与实际输出量之差为e′ss＝∞／2＝∞。

［例4-11］ 设某单位反馈系统的开环传递函数为G（s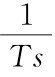）＝，试求输入信号为正弦信号r（t）＝sinωt时的稳态误差。

［解］ 根据式（4-7）可得

对应的e（t）为不收敛的三角函数信号，不适用于终值定理，故不能套用式（4-8）。