频率特性求取

按照频率特性的定义，系统频率特性可以通过如下方法求得：

（1）根据已知系统的微分方程，以正弦信号为输入，求取输出量的稳态分量和输入的正弦信号的复数之比；

（2）进行实物实验，对系统输入频率由0变化到∞的正弦信号，得到稳态输出的正弦信号，测量求得稳态输出与输入信号的幅值比和相位差。

上述两种方法都是在时间域求取系统的频率特性，须取得系统的正弦信号时域响应并截取稳态分量。其实可经过系统传递函数，不须求解全部时域解而获得稳定系统的频率特性。

图5-3中线性系统，xr（t）、xc（t）分别为系统输入和输出，设G（s）为系统传递函数，并有

输入正弦函数

xr（t）＝Asinωt

稳定系统的正弦输入的稳态响应不受初始条件影响，可以假设初始条件为零。如果Xc（s）只具有不同的极点，输出量拉氏变换可部分分式展开为

式中：bi（i＝1，2，…，n）为待定实系数；a、a－为待定的共轭复数。

Xc（s）的拉普拉斯反变换为

对于稳定的系统，－s1，－s2，…，－sn具有负实部，因而随着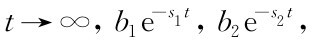…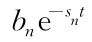，都趋于零。方程（53）除了右边第一、二项外，其余各项在稳态时都等于零。

如果Xc（s）包含有m重极点－sj，那么xc（t）将包含有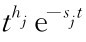（j＝0，1，2，…，m）这样的分项。由于－sj的实部为负，所以的各项随着t→∞也都趋于零。

因此，不管系统属于哪种形式，其稳态响应总为

式中：

复数G（jω）可以写成幅值∣G（jω）∣和幅角∠G（jω）的表达形式

同样

因此式（54）可写成

系统稳态输出量和输入量具有相同频率，但输出量的振幅和相位与输入量不同。

根据以上讨论，可以得到

可见，只要把系统传递函数G（s）中的算子s换成jω，就可以得到系统的频率特性

因此也可以将稳定系统的频率特性视作系统传递函数的一种特殊情况。

频率特性和传递函数是描述同一个物理系统的不同域的数学模型。微分方程是时间域的数学模型，传递函数是复数域的数学模型，而频率特性则是系统频率域的数学模型。