【摘要】:同一系统的不同状态向量之间可进行线性变换。∣λI-A∣和∣λI-P-1AP∣分别是状态变换前后的系统动态方程式特征值,系统经过线性变换后其特征值不变。对角线化就是将状态空间表达式的一般形转换为对角线标准形。对于普通形的状态空间表达式,如何通过线型变换得到对角线标准形,可参阅其他相关文献。题中给出的是能控标准形,则可取线性变换阵为
同一个系统可以有无限个状态向量,即状态向量不唯一。对应的状态空间表达式也不唯一。同一系统的不同状态向量之间可进行线性变换。
1)状态向量的线性转换
假设系统的状态方程为
 =Ax+Bu
=Ax+Bu
y=Cx+Du
令状态向量作如下线性变换
x=Pz
式中:P为非奇异线性变换阵。
则状态变换后的系统动态方程为
式中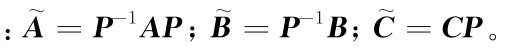
因P非奇异,乘积的行列式等于行列式的乘积,有
∣λI-A∣和∣λI-P-1AP∣分别是状态变换前后的系统动态方程式特征值,系统经过线性变换后其特征值不变。
2)能控标准形的对角线化
对角线标准形是一种常用的状态空间表达形式。对角线化就是将状态空间表达式的一般形转换为对角线标准形。以下仅给出由能控标准形化为对角线标准形。对于普通形的状态空间表达式,如何通过线型变换得到对角线标准形,可参阅其他相关文献。
一个n阶系统,设状态方程中系统矩阵A为能控标准形,且它具有两两相异的特征值λ1,λ2,…,λn。取线性变换阵P为
则变换后的矩阵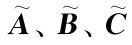 分别为
分别为
[例8-07] 设系统的状态空间表达式为
试将此系统对角线化。
[解] 由特征方程∣λI-A∣=0求出特征值为λ1=-1、λ2=-2、λ3=-3。题中给出的是能控标准形,则可取线性变换阵为
因此有
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















