用状态反馈进行极点配置，需要反馈所有状态变量。但在许多实际情况中，不是所有状态变量都能通过物理传感器检测得到，往往只有输入和输出可直接检测，此时可采用状态观测器估测各状态值以实现状态反馈。
对于式（8-11）所描述的系统，可以构造一个动态系统，以原系统的输入和输出作为它的输入，而它的状态就作为原系统状态的重构状态
，且
渐近于x，即
则称该重构系统为原系统的一个状态观测器。
可以证明：若线性定常系统完全能观，则状态变量x可由输出y和输入u进行重构。
设重构的动态系统与原系统的结构和参数均相同，即
由于状态不能直接测量，可利用输出量之间的差值
利用能检测到的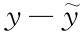
，通过输出误差反馈阵G形成校正通道，将其反馈到重构系统中，用以调整观测状态
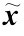，其原理框图如图8-8所示。
图8-8 状态观测器
由图8-8知重构的状态方程为
经整理后的观测器方程为
可看出观测器以原系统的输入和输出作为输入。
由式（8-11a）减去式（8-13）可得
显然要使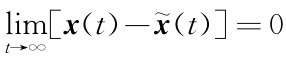
成立，则必须（A－GC）的特征值（或观测器极点）全部为负实部，即确保观测器稳定。
观测器的快速性和抗干扰性均取决于（A－GC）。因快速性和抗干扰性在一定程度上互为矛盾，故应当恰当选择观测器的极点（即A－GC的特征根），一般可取其为系统固有频率的五倍左右。
［例8-13］ 有一线性定常系统
试设计一个全维状态观测器，取观测器的极点为λ1＝－1．8＋j2．4和λ2＝－1．8－j2．4。
［解］ （1）判定系统能观性。
能观判别阵
的秩为2，故系统能观。
（2）
观测器特征方程
（3）由题中观测器的期望极点得观测器的期望特征方程为
（λ＋1．8－2．4j）（λ＋1．8＋2．4j）＝λ2＋3．6λ＋9＝0
（4）比较两特征方程，由同阶次项系数相等得g1＝29．6、g2＝3．6。
得最终的状态观测器为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
