测量误差的估计

实验或实训中经常要记录很多测量数据，这些数据应当是能反映出被测量实际大小的全部数字，即有效数字。但是在实验观测、读数、运算与最后得出的结果中，哪些是能反映被测量实际大小的数字，哪些应予以保留，哪些不应当保留，这就与有效数字及其运算法则有关。前面已经指出，测量不可能得到被测量的真实值，只能是近似值。实验数据的记录反映了近似值的大小，并且在某种程度上表明了误差。因此，有效数字是对测量结果的一种准确表示，它应当是有意义的数码，而不允许无意义的数字存在。如果把测量结果写成54．2817 ±0．05(cm)是错误的，由不确定度0．05(cm)可以得知，数据的第二位小数0．08已不可靠，把它后面的数字也写出来没有多大意义，正确的写法应当是: 54．28±0．05(cm)。测量结果的正确表示，对初学者来说是一个难点，必须加以重视，多次强调，才能逐步形成正确表示测量结果的良好习惯。

1．有效数字的概念

任何一个物理量，其测量的结果都或多或少地有误差，那么一个物理量的数值就不应当无止境地写下去，写多了没有实际意义，写少了又不能比较真实的表达物理量。因此，一个物理量的数值和数学上的某一个数就有着不同的意义，这就引入了一个有效数字的概念。若用最小分度值为1mm的米尺测量物体的长度，读数为5．63cm。其中5和6这两个数字是从米尺的刻度上准确读出的，可以认为是准确的，叫做可靠数字。末尾数字3是在米尺最小分度值的下一位上估计出来的，是不准确的，叫做欠准数。虽然是欠准可疑，但不是无中生有，而是有根有据有意义的，显然有一位欠准数字，就使测量值更接近真实值，更能反映客观实际。因此，测量值应当保留到这一位是合理的，即使估计数是0，也不能舍去。测量结果应当而且也只能保留一位欠准数字，故测量数据的有效数字定义为几位可靠数字加上一位欠准数字称为有效数字，有效数字的个数叫做有效数字的位数，如上述的5．63cm称为三位有效数字。

有效数字的位数与十进制单位的变换无关，即与小数点的位置无关。因此，用以表示小数点位置的0不是有效数字。当0不是用作表示小数点位置时，0和其他数字具有同等地位，都是有效数字。显然，在有效数字的位数确定时，第一个不为零的数字左面的零不能算有效数字的位数，而第一个不为零的数字右面的零一定要算做有效数字的位数。如0．0135m是三位有效数字，0．0135m和1．35cm及13．5mm三者是等效的，只不过是分别采用了米、厘米和毫米作为长度的表示单位; 1．030m是四位有效数字。从有效数字的另一面也可以看出测量用具的最小刻度值，如0．0135m是用最小刻度为毫米的尺子测量的，而1．030m是用最小刻度为厘米的尺子测量的。因此，正确掌握有效数字的概念对物理实验来说是十分必要的。

2．直接测量的有效数字记录

实验或实训中通常仪器上显示的数字均为有效数字(包括最后一位估计读数)，都应读出，并记录下来。仪器上显示的最后一位数字是0时，此0也要读出并记录。对于有分度式的仪表，读数要根据人眼的分辨能力读到最小分度的十分之几。在记录直接测量的有效数字时，常用一种称为标准式的写法，就是任何数值都只写出有效数字，而数量级则用10的n次幂的形式去表示。

(1)根据有效数字的规定，测量值的最末一位一定是欠准确数字，这一位应与仪器误差的位数对齐，仪器误差在哪一位发生，测量数据的欠准位就记录到哪一位，不能多记，也不能少记，即使估计数字是0，也必须写上，否则与有效数字的规定不相符。例如，用米尺测量物体长为52．4mm与52．40mm是不同的两个测量值，也是属于不同仪器测量的两个值，误差也不相同，不能将它们等同看待，从这两个值可以看出测量前者的仪器精度低，测量后者的仪器精度高出一个数量级。

(2)根据有效数字的规定，凡是仪器上读出的数值，有效数字中间与末尾的0，均应算作有效位数。例如，6．003cm、4．100cm均是四位有效数字; 在记录数据中，有时因定位需要，而在小数点前添加0，这不应算作有效位数，如0．0486m是三位有效数字而不是四位有效数字，有效数字中的0有时算做有效数字，有时不能算做有效数字，这对初学者也是一个难点，要正确理解有效数字的规定。

(3)根据有效数字的规定，在十进制单位换算中，其测量数据的有效位数不变，如4．51 cm若以米或毫米为单位，可以表示成0．0451m或45．1mm，这两个数仍然是三位有效数字。为了避免单位换算中位数很多时写一长串，或计数时出现错位，常采用科学表达式，通常是在小数点前保留一位整数，用10n表示，如4．51×102m，4．51×104cm等，这样既简单明了，又便于计算和确定有效数字的位数。

(4)根据有效数字的规定对有效数字进行记录时，直接测量结果的有效位数的多少，取决于被测物本身的大小和所使用的仪器精度。对同一个被测物，高精度的仪器测量的有效位数多，低精度的仪器测量的有效位数少。例如，长度约为3．7cm的物体，若用最小分度值为1mm的米尺测量，其数据为3．70cm，若用螺旋测微器测量(最小分度值为0．01mm)，其测量值为3．7000cm，显然螺旋测微器的精度较米尺高很多，所以测量结果的位数也多; 被测物是较小的物体，测量结果的有效位数也少。对一个实际测量值，正确应用有效数字的规定进行记录，就可以从测量值的有效数字记录中看出测量仪器的精度。因此，有效数字的记录位数和测量仪器有关。

3．有效数字的运算法则

在进行有效数字计算时，参加运算的分量可能很多。各分量数值的大小及有效数字的位数也不相同，而且在运算过程中，有效数字的位数会越乘越多，除不尽时有效数字的位数也无止境。即便是使用计算器，也会遇到中间数的取位问题以及如何更简洁的问题。测量结果的有效数字，只能允许保留一位欠准确数字，直接测量是如此，间接测量的计算结果也是如此。根据这一原则，为了达到: ①不因计算而引进误差，影响结果; ②尽量简洁，不作徒劳的运算。简化有效数字的运算，约定下列规则:

(1)加法或减法运算。

大量计算表明，若干个数进行加法或减法运算，其和或者差的结果的欠准确数字的位置与参与运算各个量中的欠准确数字的位置最高者相同。由此得出结论，几个数进行加法或减法运算时，可先将多余数修约，将应保留的欠准确数字的位数多保留一位进行运算，最后结果按保留一位欠准确数字进行取舍。这样可以减小繁杂的数字计算。

推论一: 若干个直接测量值进行加法或减法计算时，选用精度相同的仪器最为合理。

(2)乘法和除法运算。

由此得出结论: 用有效数字进行乘法或除法运算时，乘积或商的结果的有效数字的位数与参与运算的各个量中有效数字的位数最少者相同。

推论二: 测量的若干个量，若是进行乘法或除法运算，应按照有效位数相同的原则来选择不同精度的仪器。

(3)乘方和开方运算。

由此可见，乘方和开方运算的有效数字的位数与其底数的有效数字的位数相同。

(4)自然数1，2，3，4，…不是测量而得，不存在欠准确数字。因此，可以视为无穷多位有效数字的位数，书写也不必写出后面的0，如D=2R，D的位数仅由直测量R的位数决定。

(5)无理常数π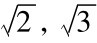，，…的位数也可以看成很多位有效数字。例如L=2πR，若测量值R=2．35×10－2(m)时，π应取为3．142。则

L=2×3．142×2．35×10－2=1．48×10－1(m)

(6)有效数字的修约。根据有效数字的运算规则，为使计算简化，在不影响最后结果应保留有效数字的位数(或欠准确数字的位置)的前提下，可以在运算前、后对数据进行修约，其修约原则是“四舍六入五看右左”。五看右左即为五时则看五后面的数，若为非零的数则入; 若为零则往左看拟留数的末位数，为奇数则入为偶数则舍。中间运算过程较结果要多保留一位有效数字。