【摘要】：在一般情况下，真实值是不易知道的，故常用精确度来判断分析数据的好坏。对精确度的系统评价通常用标准偏差和变异系数来表示。因此，比较两者标准偏差的差异，可以看出标准偏差越大，数据的离散程度就越高，精确度越差。除了标准偏差，变异系数是评价分析数据精确度的直观方法，可通过式进行计算。在本例中，变异系数已远超过5%，因此，该重复结果的精确度和重现性均较差，仪器操作或实验过程存在需改进地方。
在一般情况下，真实值是不易知道的，故常用精确度来判断分析数据的好坏。对精确度的系统评价通常用标准偏差(standard deviation)和变异系数(coefficient variation)来表示。
假设对某一指标重复测定了n次，那么标准偏差可用式(14-4)来计算。
式中: σ——标准偏差;
μ——真实值;
xi——各个样品测量值;
n——样品个数。
在(14-4)中，由于真实值μ未知，所以一般用平均值x¯代替μ，σ则用样品标准偏差SD代替。因此，式(14-4)可简化为式(14-5)。
在一般情况下，我们进行指标测定时，重复次数一般少于30，即n＜30，此时n可用(n-1)代替，因此，式(14-5)变为式(14-6)。
以14．1．3中的面包水分测定数据为例，因为n=5＜30，其标准偏差可通过式(14-6)进行计算。在前面我们已算出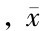
=54．62%，由此算出
但如果我们将41．72%这一测定数值改为51．72%，其平均值x¯=56．62%，由此算出SD=3．45。因此，比较两者标准偏差的差异，可以看出标准偏差越大，数据的离散程度就越高，精确度越差。
除了标准偏差，变异系数(即相对标准偏差)是评价分析数据精确度的直观方法，可通过式(14-7)进行计算。仍以面包水分的测定为例，其变异系数计算如下:
虽然不同类型的分析对变异系数的要求不同，但在一般情况下，变异系数小于5%时，可认为重复结果的精确度和重现性水平均很高。在本例中，变异系数已远超过5%，因此，该重复结果的精确度和重现性均较差，仪器操作或实验过程存在需改进地方。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
