对数的运算教学设计

对数的运算教学设计

赵志禄

【课　　题】2.2.1对数与对数的运算

【教学内容】对数的运算法则及其应用

【三维目标】

一、知识与技能

掌握对数的运算法则，能熟练地利用法则解决有关对数式的化简、求值问题。

二、过程与方法

1.利用类比的方法，得出对数的运算法则，让学生体会到数学知识的前后连贯性，加深对公式内容及公式适用条件的记忆。

2.通过探究、思考、培养学生理性思维能力、观察能力以及判断能力。

三、情感态度与价值观

1.通过师生、生生之间的相互交流，使学生加深对数运算法则的理解，增强学生的数学交流能力和数学的分析问题的能力。

2.通过对数运算的学习，使学生明确数学概念的来龙去脉，体会知识间的相互联系，感受数学的整体性。

【教学重点】对数运算法则及应用

【教学难点】对数运算法则的逆用

【教具准备】多媒体（PPT）

【教学流程】

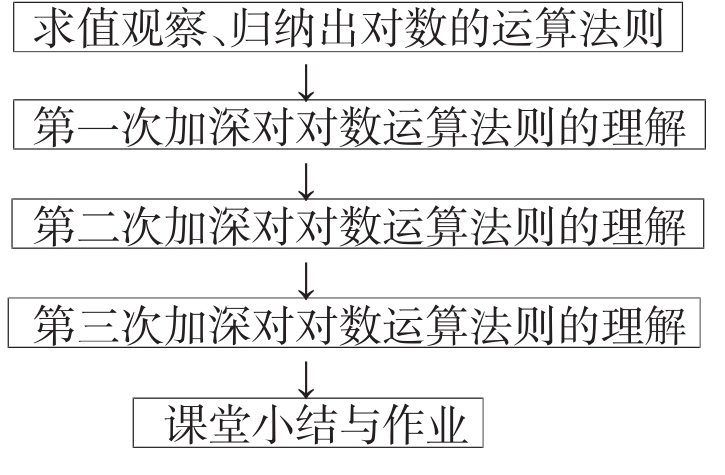
【教学过程】

一、创设情景，引入新课

师：上节课，我们学习了对数的概念，对数与指数的互化，对数的恒等式等，哪位同学能简要地说一说它们吗？（复习旧知，知道联系，为后面新知的学习埋下伏笔）

生：略（师板书：若a^b=N，则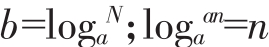 a＞0且a≠1）

师：对数的含义是什么？（使学生意识到对数应该具有指数的运算法则）

生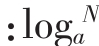就表示a的多少次方是N，实际就是指数。

师：同底数幂运算有哪些法则，对数有吗？（引发学生思考）

点题、板书课题

二、讲解新课。

1、投影幻灯片一（使学生对对数的运算法则有一个感性认识）

投影一、计算下列各组对数的值，并观察归纳其规律。

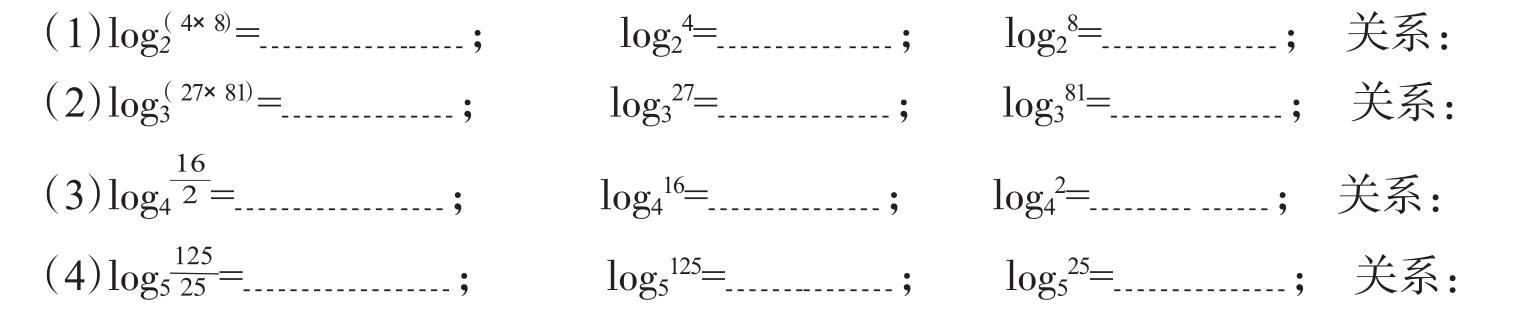
师：就以上各式中发现的关系，谁能用一般式表示出来吗？

师：就这样吗？这里的,M,N没有任何范围限制吗？

生：a＞0且≠1,M＞0，N＞0

师：它们的适用范围千万不能丢，当然，它的真伪我们也不能用特殊来代替一般，还需要进行一般性证明，谁给大家演示一下证明过程。

生：略

师：追本溯源，利用旧知解决新问题，变未知为已知是我们解决问题时经常要采用的方法之一，这种思想也是重要的数学思想之一，大家一定要灵活应用，好，下面再看一看，若a＞0且a≠1，b＞0那么，为什么？

2.投影幻灯片二（初步尝试运算法则的应用）

（生板演）

师：（讲评学生板演，强调书写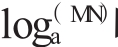时一定要把MN用“（　）”括住），请同学们看下列问题会解吗，投影幻灯（希望能逆用运算法则）

投影三：

1.求下列各式的值

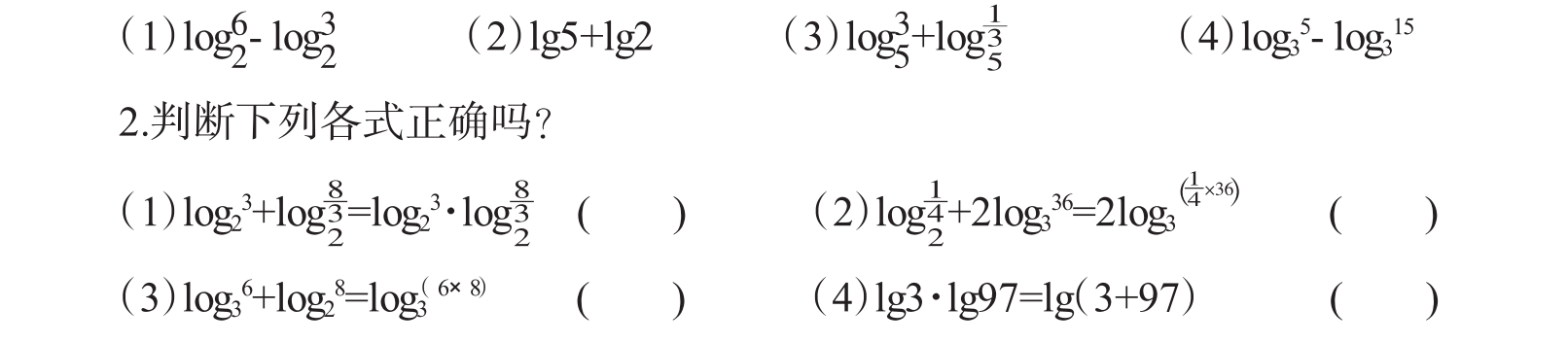
生：板演第一题

师：讲评完第一题后（提问让学生口答第2题，老师再次强调应用法则时的注意事项，并投影幻灯）。（希望学生能熟练逆用公式，加深对法则的理解）

投影4：

求下列各式的值

例2：（1）3lg5+3lg2　　（2）2lg5+lg4　　（3）lg14-2lg+lg7-lg18　　（4）（lg5）²+lg2lg5+lg2

生：板演

师：讲评学生解答之后小结

三、课内小结

1.让学生概述本节所学知识与方法

2.师强调：

（1）对数的运算法则是有范围限制的，a＞0且a≠1，M＞0 N＞0；

（2）逆用对数的运算法则时，对数的系数和指数必须是1，并且底数相同，如果对数的系数不是1，就要用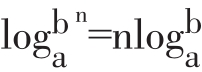^（a＞0且a≠1，b＞0）将系数化为1，如果对数的指数不是1，就要用分解因式等方法降幂。

（3）在理解对数的运算法则时，只要把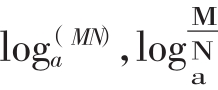分别理解成同底数的两个幂的积和商的指数，就会联想到同底数幂相乘（除），底数不变，指数相加（减），自然也就记住对数的运算法则了。

四、布置作业

1.课本P82，习题2.2 A组3，4,5

2.预习课本P72～P74内容

【板书设计】