两个代数猜想不等式的证明及推广

两个代数猜想不等式的证明及推广

马占山

文［1］提出了如下一个轮换代数不等式，即文［1］中的LBQ109设x₁∈R⁺，（i=1，2，3，4），则有

本文旨在给出这个猜想成立的证明及其推广。

1.证明：不等式（1）等价于

设a，b，c，d∈R⁺且，则有

（2）［（1+b）（1+c）（1+d）］²+［（1+a）（1+c）（1+d）］²+［（1+a）（1+b）（1+d）］²+［（1+a）（1+b）（1+c）］²≥［（1+a）（1+b）（1+c）（1+d）］²（3）

为计算上的方便，这里应用如下一个恒等式

（x+y+z+w）²=x²+y²+z²+w²+2xy+2xz+2xw+2yz+2yw+2zw

因而给（3）的两边都加上：

2（1+a）（1+b）（1+c）（1+d）［（1+a）（1+b）（1+a）（1+c）（1+a）（1+d）（1+b）（1+c）（1+b）（1+d）（1+c）（1+d）］

（3）的左边=［（1+b）（1+c）（1+d）（1+a）（1+c）（1+d）（1+a）（1+b）（1+d）（1+a）（1+b）（1+c）］²=［（4+3）（a+b+c+d）+2（ab+ac+ad+bc+bd+cd）+（abc+bcd+cda+dab）］²

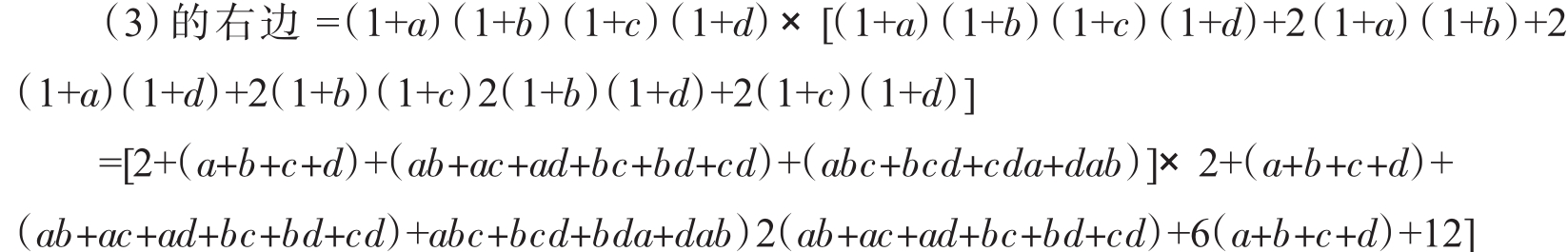
令a+b+c+d=m，ab+ac+ad+bc+bd+cd=n，abc+bcd+cda+dsb=p

（3）的右边=（m+n+p+2）（7m+3n+p+14）=7m²+3n²+p²+10mn+8mp+4np 28m+20n+16p+28

（3）的左边=（3m+2n+p+4）²=9m²+4n²+p²+12mn+6mp+4np+24m+16n+8p+16

记M=（3）的左边—（3）的右边。故有：

M=2m²+n+2mn-2mp-4n-8p-12

M=2m²+n²+2mn+2mp-4m-4n-8p-12

故只需证M≥0成立即可。

由于n²=（ab+ac+ad+bc+bd+cd）²=（a²b²+a²c²+a²d²+b²c²+b²d²+c²d²）+2（a²bc+ab²c+abc²）2（b²cd+bc²d+bcd²）+2（c²da+cd²a+cda²）+2（d²ab+da²b+dab²）+6

而2mp=2（a+b+c+d）（abc+bcd+dab）=2（a²bc+ab²c+abc²）2（b²cd+bc²d+bcd²）+2（c²da+cd²a+cda²）+2（d²ab+da²b+dab²）+8

则：n²-2mp=（a²b²+a²c²+a²d²+b²c²+b²d²+c²d²）-2

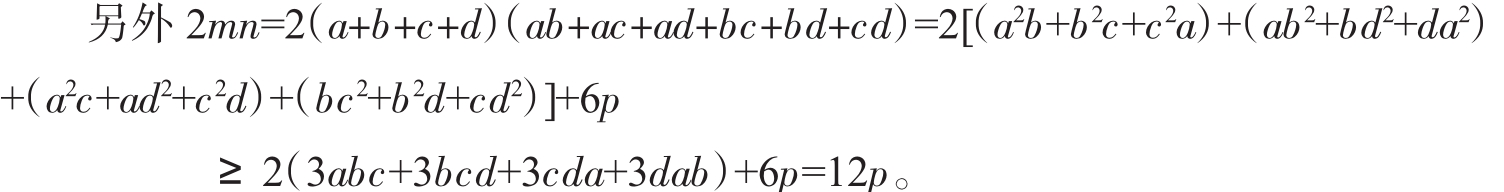
故　2mn-8p≥4p；又显然有m²-4m≥0。

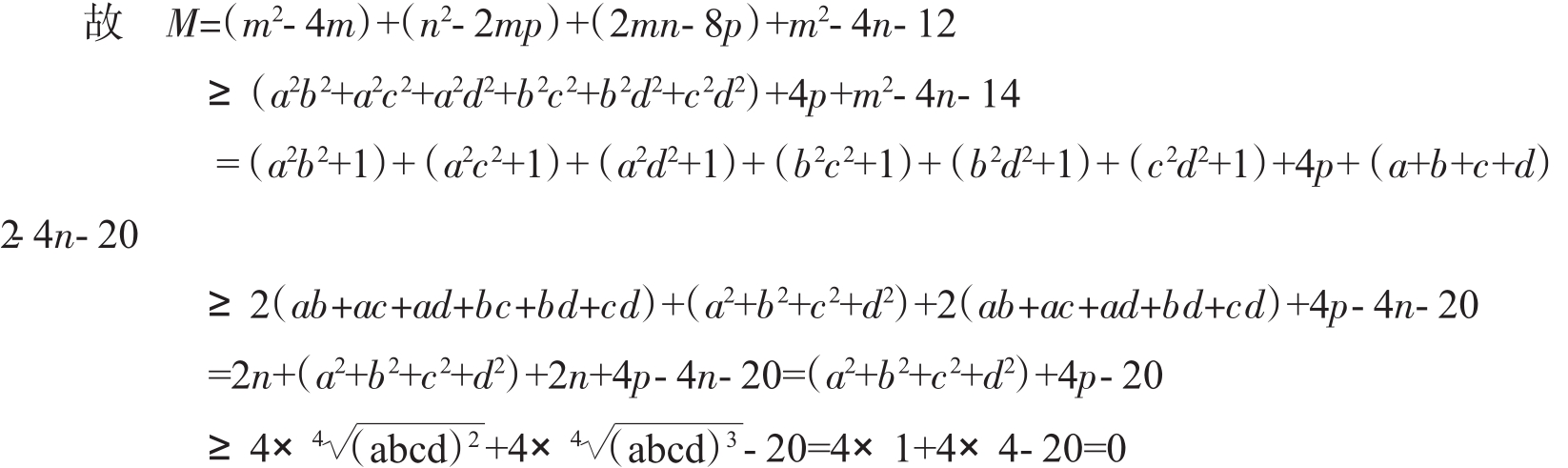
当且仅当a=b=c=d=1时等式成立。进而当且仅当x₁=x₂=x₃=x₄时不等式（1）取到等号。

2.推广1：设x₁，x₂，x₃，x₄ R⁺，则有：

证明：在幂平均不等式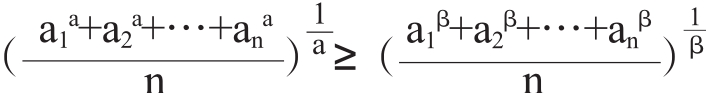中，（a＞β＞0，a₁ R⁺，i=1，2，3，4）令a₁=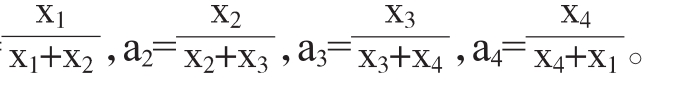

取β=2，n=4，再结合不等式（1）即要得证。

文［1］给出如下另一猜想不等式：

下面笔者给出不等式（1）的证明，然后再给出其推广。

证明：令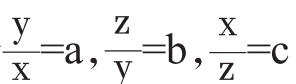，则不等式（1）等价于

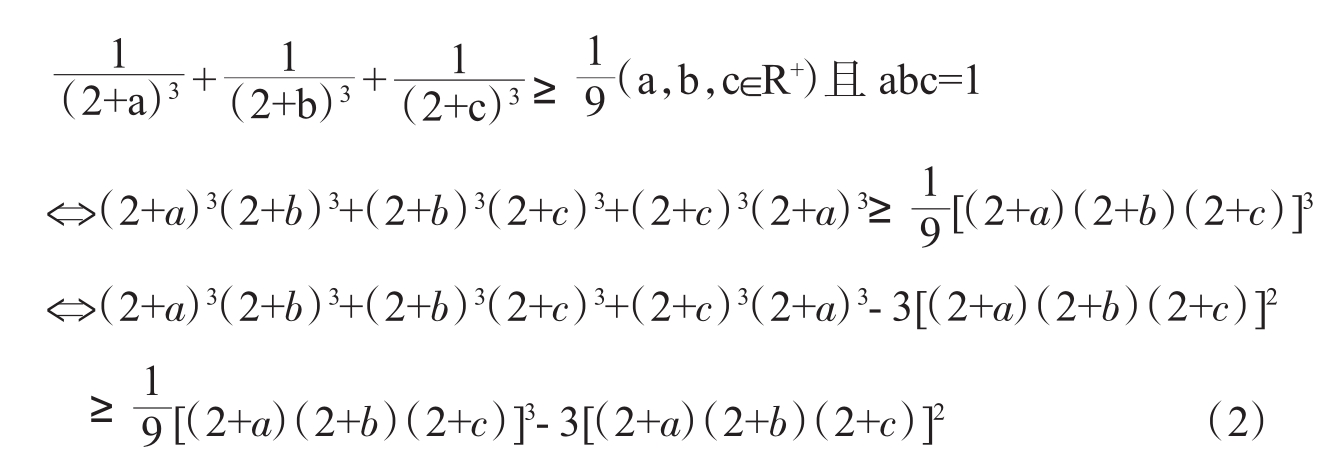
应用恒等式m³+n³+p³-3mnp=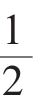（m+n+p）［（m-n）²+（n-p）²+（p-m）²］，不等式（2）的左边可化为

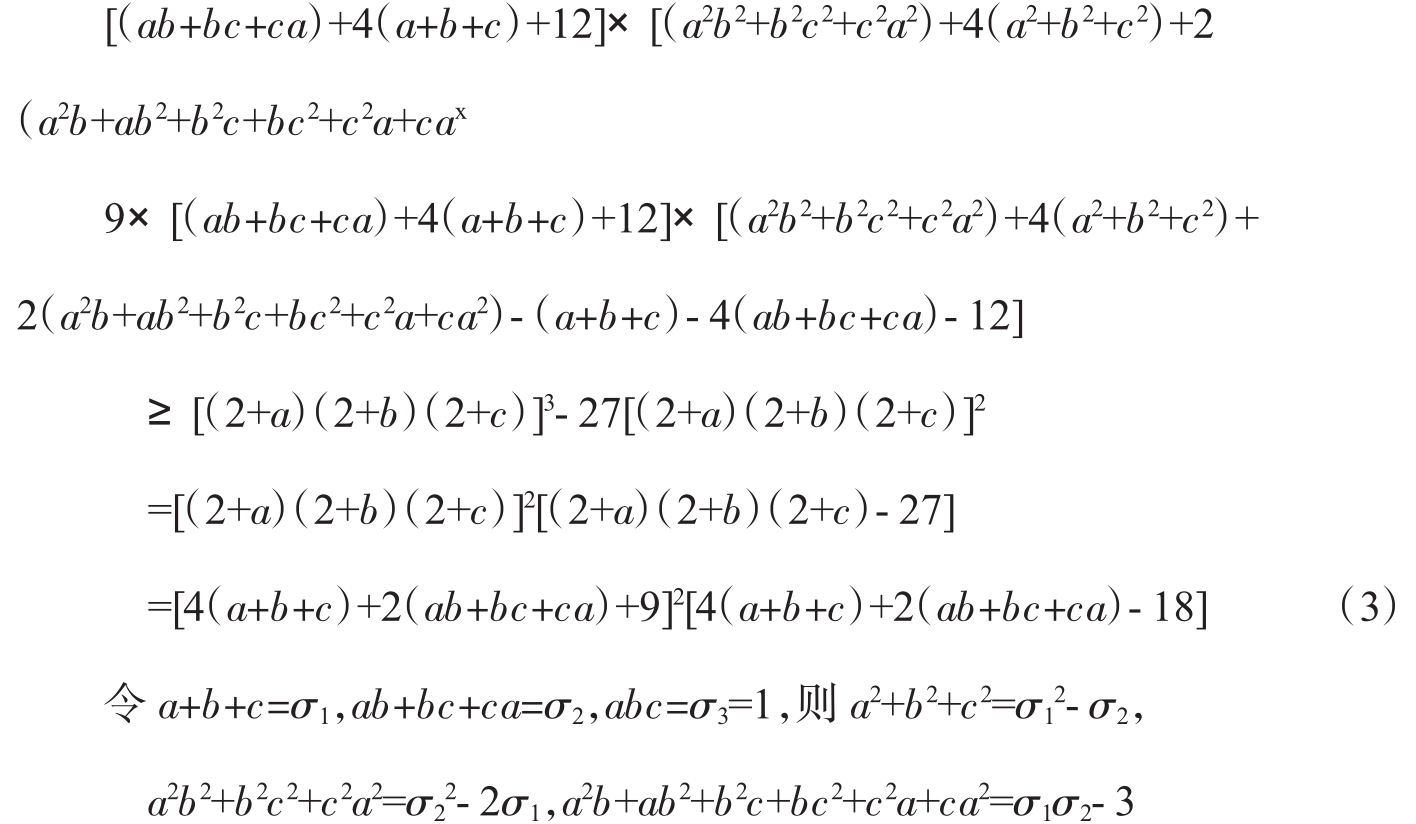
从而不等式（3）即可

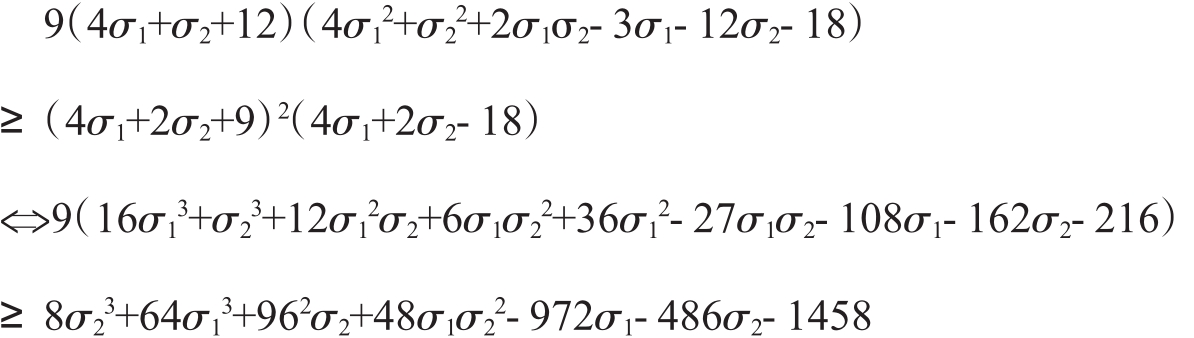
左、右相减得

从而只需证（4）式即可。

∵σ₂=ab+bc+ca≥3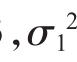=（a+b+c）²≥3（ab+bc+ca）=3σ₂≥9

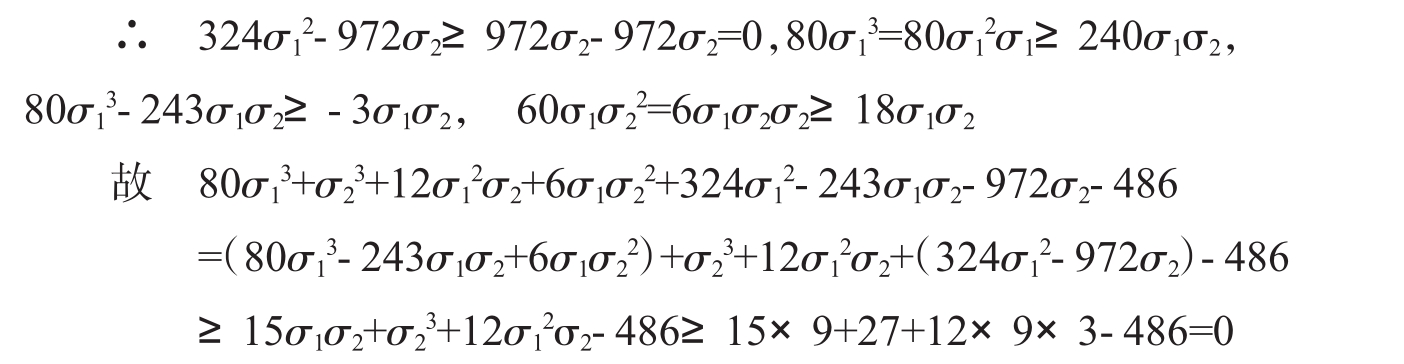
不等式（2）等号成立的条件是当且仅当a=b=c=1，进而不等式（1）等号成立的条件是当且仅当x=y=z。

证明：在幂平均不等式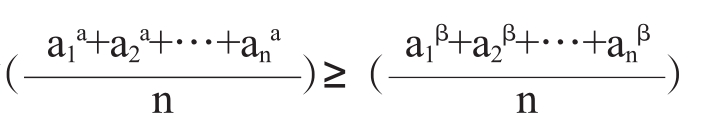

（α＞β＞0，ai∈R⁺，i=1，2，…，n）中，令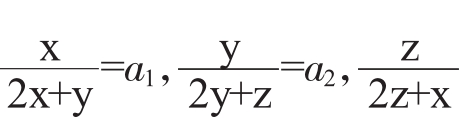 =a₃，β=3，再结合不等式（1）即可得证。

参考文献

刘保乾.110个有趣的不等式问题LBQ109，LBQ107.不等式研究.西藏人民出版社，404.

此文发表于《中学数学研究》