等差递减数列前项和最大值求法

等差递减数列前n项和最大值求法

刘春杰

2008年宁夏高考试题17题：

已知{a_n}是一个等差数列，且a₂=1，a₅=-5.

（1）略.

（2）求{a_n}前n项s_n的最大值.

一、试题解答

解法一：a₅-a₂=（5-2）d=-6，d=-2于是求得a₁=3，a₃=-1＜0。以后各项是负数，因此s₂=a₁+a₂=4为最大。

解法二：a_n=a₁+（n-1）d=-2n+5

可见n=2时，S_n最大为S₂=4。

二、解法提炼

对于首项为正数的等差递减数列前面所有的正数项和为最大，为此，我们只需判断{a_n}中

方法一：（1）a_m=0时，s_m=s_m-1为最大；

　　　　（2）a_m＞0，a_m+1＜0时s_m最大，特别的，能写出通项a_m=dm+a（d为公差，a为常数）。

由a_m＞0得dm+a＞0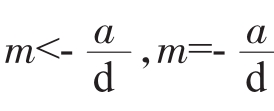时，s_m最大。

方法二：s_n是n的二次函数，可利用二次函数及图象的性质确定最大值及n的值。

三、方法应用

例1：等差数列{a_n}中，a₁₀=62，a₂₀=22，求数列{a_n}的前n项和最大值。

解：a₂₀-a₁₀=（20-10）d=-40

　　d=-4，可求出a₁=98

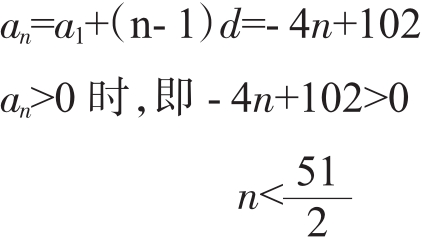
取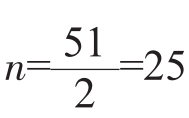时，S₂₅最大。

另解：s_n=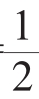（a₁+a_n）n=-2（n-25）²+1250，可见n=25时S_max=S₂₅=1250

例2：设等差数列{a_n}满足3a₈=5a₁₃且a₁＞0，S_n为前n项和，求S_n最大时的n值。

另解：由2a₁+39d=0，知a₁+（a₁+39d）=0即a₁+a₄₀=0,S₄₀=0。

由S₀=S₄₀=0，结合二次函数图象的对称性知S₂₀最大，n=20。

例3：在等差数列{a_n}中，S₁₂＞0，S₁₃＜0，问S₁，S₂，…，S_n中哪个最大？

解：S₁₂=6（a₁+a₂）=6（a₆+a₇）＞0

由此可知：a₆＞0，a₇＜0，说明S₆最大。