《平行线的性质》教学设计
陈亚琴
一、教学目标
知识与技能:掌握平行线的性质,能应用性质解决相关问题。
数学思考:在平行线的性质的探究过程中,让学生经历观察、比较、联想、分析、归纳、猜想、概括的全过程。
解决问题:通过探究平行线的性质,使学生形成数形结合的数学思想方法,以及建模能力、创新意识和创新精神。
情感态度与价值观:在探究活动中,让学生获得亲自参与研究的情感体验,从而增强学生学习数学的热情和勇于探索、锲而不舍的精神。
二、教学重点、难点
1.教学重点:平行线的性质
2.教学难点:“性质1”的探究过程
三、教学方法
“引导发现法”与“动像探索法”
四、教具、学具
1.教具:多媒体课件。
2.学具:三角板、量角器。
五、教学过程
(一)创设情境,设疑激思
1.播放一组幻灯片。内容:①火车行驶在铁轨上;②游泳池;③横格纸。
2.声音:日常生活中我们经常会遇到平行线,你能说出直线平行的条件吗?
学生思考后回答:
①同位角相等两直线平行;
②内错角相等两直线平行;
③同旁内角互补两直线平行。
教师首先肯定学生的回答,然后提出问题:若两直线平行,那么同位角、内错角、同旁内角各有什么关系呢?
(二)数形结合,探究性质
1.画图探究,归纳猜想
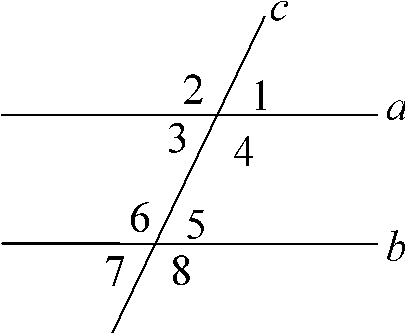
任意画出两条平行线(a∥b),画一条截线c与这两条平行线相交,标出8个角(如图)。
问题一:指出图中的同位角,并度量这些角,把结果填入下表:
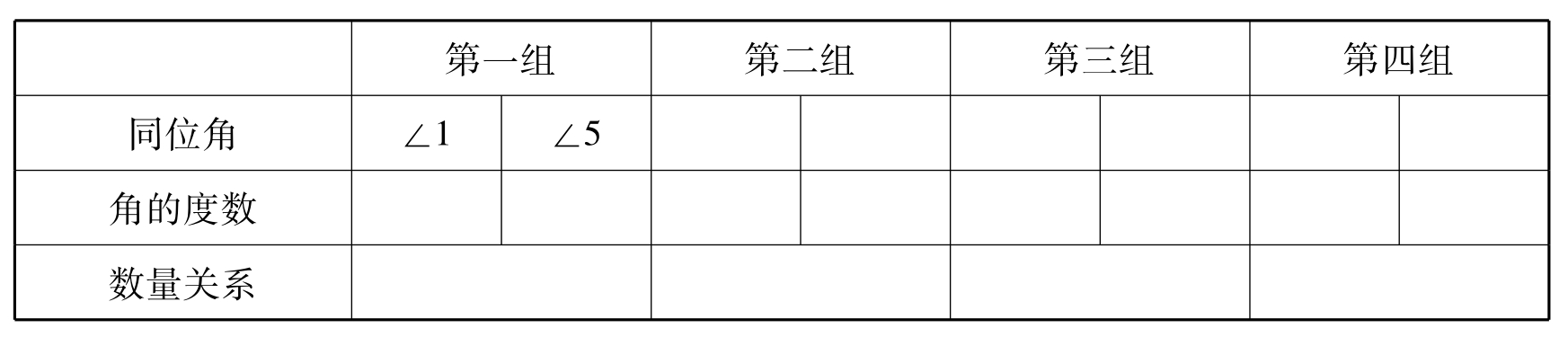
学生活动:画图——度量——填表——猜想
结论:两直线平行,同位角相等。
问题二:再画出一条截线d,看你的猜想结论是否仍然成立?
学生:探究、讨论,最后得出结论:仍然成立。
2.教师用《几何画板》课件验证猜想
3.性质1.两条直线被第三条直线所截,同位角相等。(两直线平行,同位角相等)
(三)引申思考,培养创新
问题三:请判断内错角、同旁内角各有什么关系?
学生活动:独立探究——小组讨论——成果展示。
教师活动:评价,引导学生说理。
因为a∥b 因为a∥b
所以∠1=∠2 所以∠1=∠2
又∠1=∠3 又∠1+∠4=180°
所以∠2=∠3 所以∠2+∠4=180°
语言叙述:
性质2 两条直线被第三条直线所截,内错角相等。
(两直线平行,内错角相等)
性质3两条直线被第三条直线所截,同旁内角互补。
(两直线平行,同旁内角互补)
(四)实际应用,优势互补
1.如图1,平行线AB、CD被直线EF所截
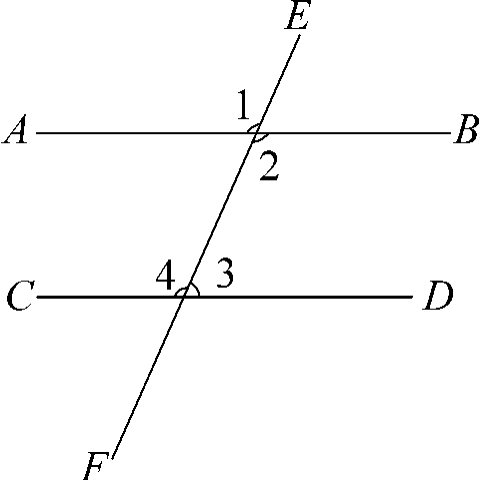
图1
(1)(抢答)
①若∠1=110°,则∠2=______。理由:________。
②若∠1=110°,则∠3=______。理由:________。
③若∠1=110°,则∠4=______。理由:________。
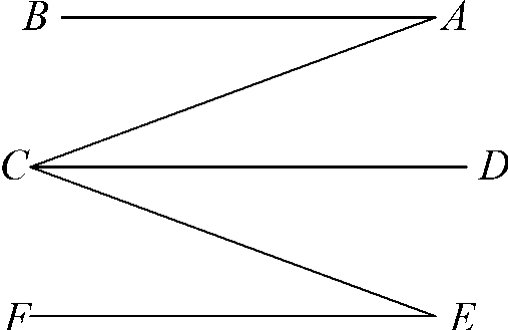
图2
(2)如图1,由AB∥CD,可得()
A.∠1=∠2 B.∠2=∠3
C.∠1=∠4 D.∠3=∠4
(3)如图2,AB∥CD∥EF,
那么∠BAC+∠ACE+∠CEF=()
A.180° B.270° C.360° D.540°
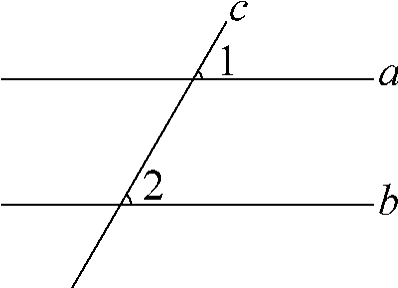
图3
(4)谁问谁答:如图3,直线a∥b,
如:∠1=54°时,∠2=________.
学生提问,并找出回答问题的同学。
2.(讨论解答)
如图4是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,求梯形另外两角分别是多少度?
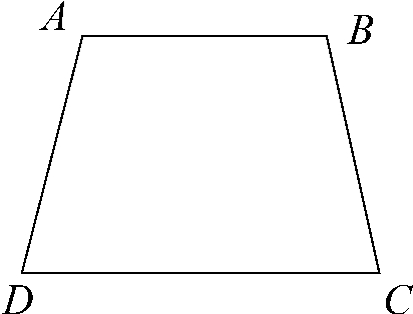
图4
(五)概括存储(小结)
1.平行线的性质①②③;
2.用“运动”的观点观察数学问题;
3.用数形结合的方法来解决问题。
六、教学反思
1.教的转变
本节课教师的角色从知识的传授者转变为学生学习的组织者、引导者、合作者与共同研究者。在引导学生画图、测量、发现结论后,利用几何画板直观地、动态地展示同位角的关系,激发学生自觉地探究数学问题,体验发现的乐趣。
2.学的转变
学生的角色从学会转变为会学。本节课学生不是停留在学会课本知识的层面上,而是站在研究者的角度深入其境。
3.课堂氛围的转变
整节课以“流畅、开放、合作、‘隐’导”为基本特征,教师对学生的思维活动减少干预,教学过程呈现一种比较流畅的特征,整节课学生与学生、学生与教师之间以“对话”“讨论”为出发点,以互助、合作为手段,以解决问题为目的,让学生在一个较为宽松的环境中自主选择获得成功的方向,判断发现的价值。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















