三角形的两角与全等的相似

《探索三角形相似的条件（一）》教学设计

刘　雪

一、教学目标

1.知识目标：探索两个三角形相似的条件，并会用相似三角形的判定方法（一）来判断和计算。

2.能力目标：通过运用三角形相似的条件解决简单问题，进一步发展合情推理能力和初步的逻辑推理能力。

3.情感目标：在直观感觉——动手感知——理性思维——应用拓展的活动中，开发、培养学生的发散性思维，进一步发展学生的探究、合作交流意识，以及动手、动脑和谐一致的习惯。

二、教学重点、难点

教学重点：三角形相似的条件1的探索与应用。

教学难点：条件的应用及找相等的两组对应角。

三、教学方法

引探式的教学法。教师着眼于引导，学生着眼于探索。其主要流程可以分为“直觉观察——实验探究——讨论交流——应用拓展”

四、教学过程

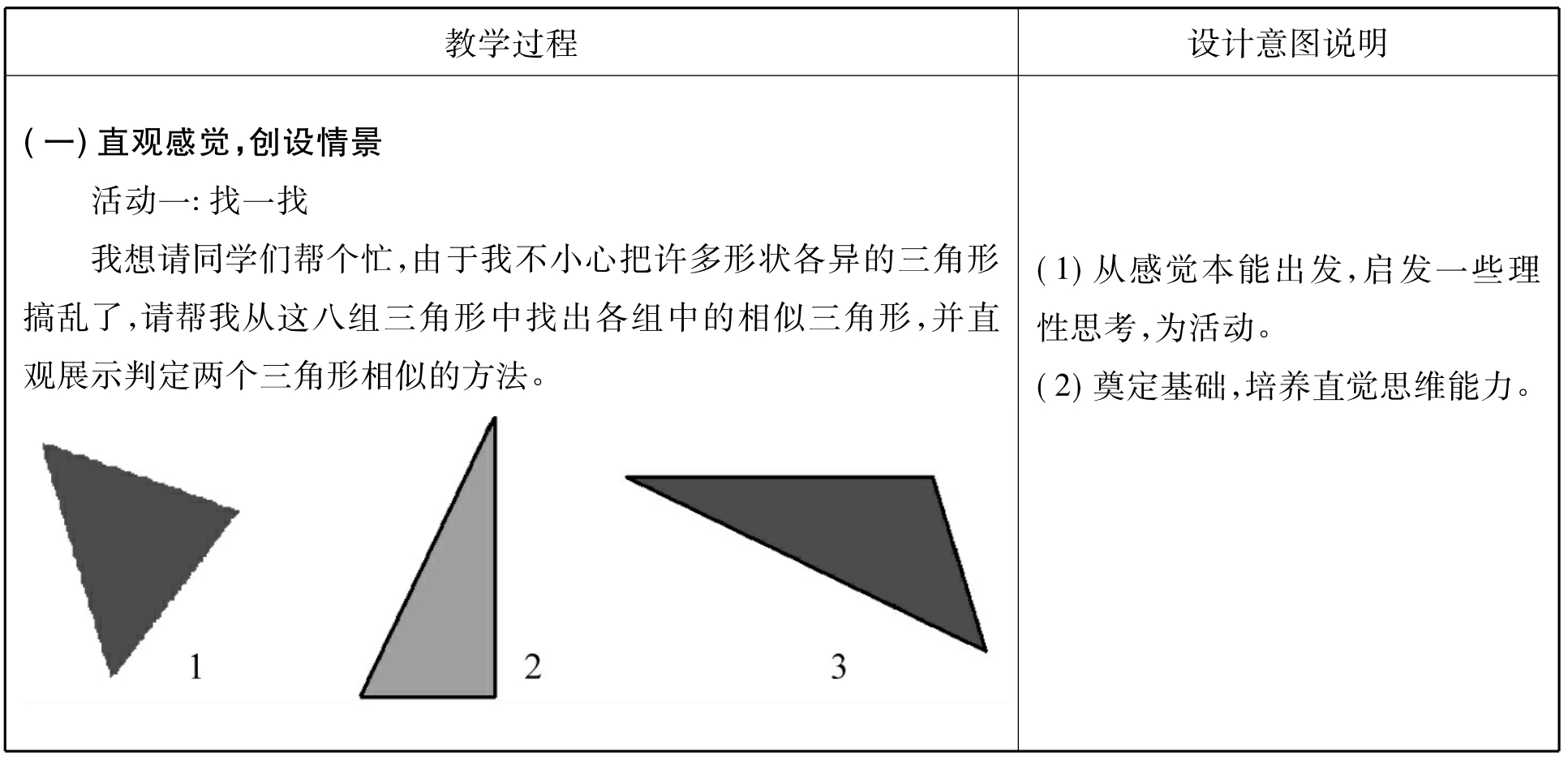
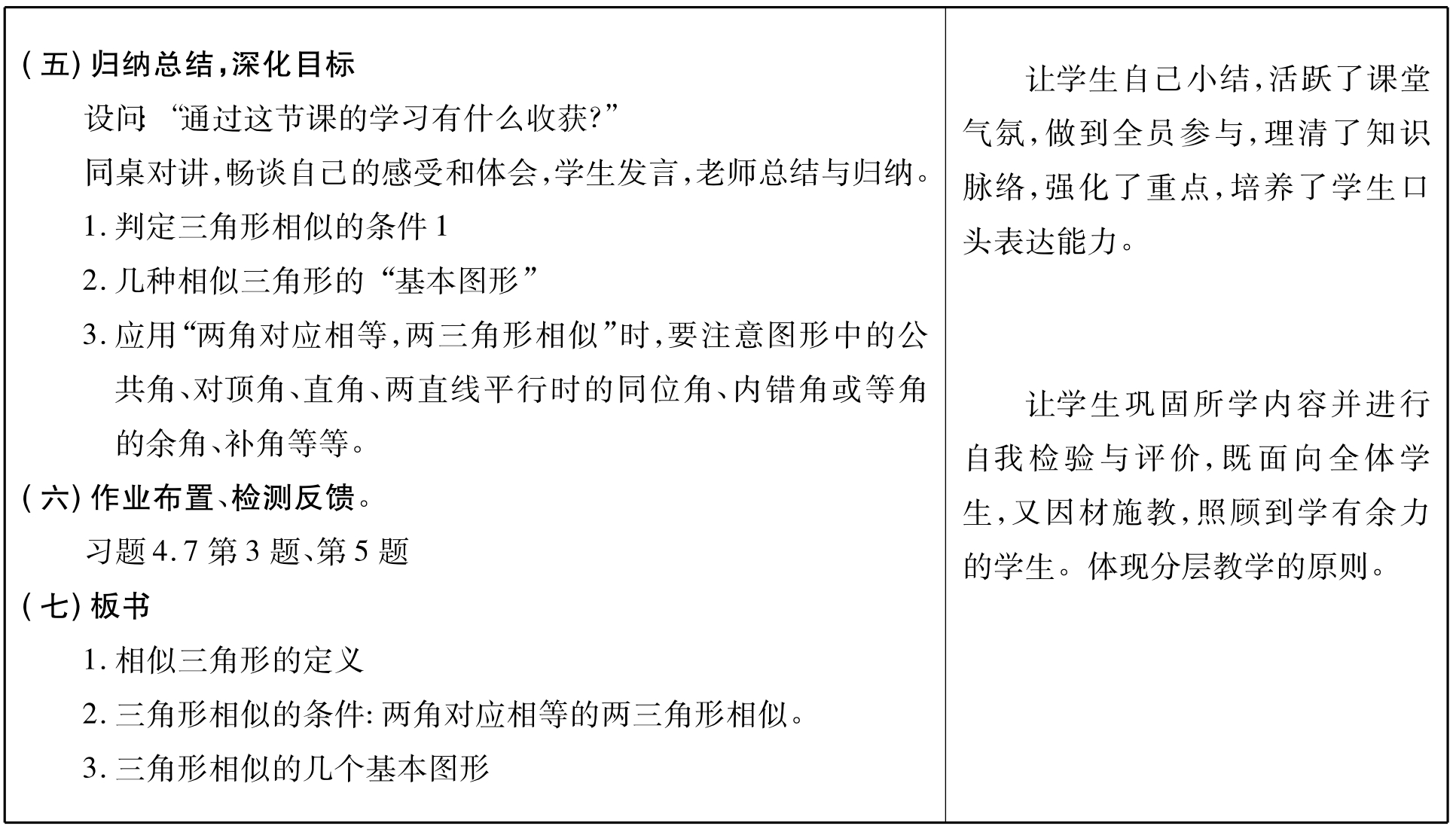
五、教学反思

校外公开课我讲的是《探索三角形相似的条件（1）》一课，本节课的主要内容是“如果一个三角形的两角与另一个三角形的两角对应相等，那么这两个三角形相似。”应该说本节课的知识是学生比较容易掌握的，但为了更好地体现知识目标、能力目标、情感目标，能更好地培养学生的思维能力，养成良好的研究习惯，在本节课的教学中，根据《新课标》的要求，我从数学研究的一般思路“猜想—验证—说理—应用”进行了知识形成过程的教学。下面谈谈教学过程的得与失。

（一）提出猜想

我们知道，两个三角形全等的判定条件有角角边、角边角，而全等三角形是相似比为1的特殊的相似三角形，综合这二者，可以从以下两个层次做进一步的思考。

第一个层次：全等的两个三角形除了是全等关系，还是相似关系。

第二个层次：相似三角形对边的要求比全等三角形对边的要求要宽松。但对角的要求是同等的。

在以上两个层次的研究基础上，提出科学、大胆的猜想：在较少条件下，即一个三角形的两角与另一个三角形的两角对应相等，那么这两个三角形是否相似呢？

猜想并不是胡想乱想，它的提出需要学生对已有的知识和所需探究的知识有很深刻的理解，很深的洞察力。光有知识是远远达不到要求的。上面猜想的提出就是一个很好的例子，如果不能理解出上面的两层含义，就不会有这样科学、合理的猜想。在这猜想提出的过程中，学生会更清楚全等和相似两者之间的关系（特殊与一般的关系），也会在无意间感受、运用着类比和从特殊到一般的数学研究方法。

实际教学中，好多同学敢于提出自己的猜想。

（二）测量验证

猜想对吗？我们需要对它做出一个判断。测量法、特殊值法等都是很好的验证方法。图形问题则是测量法的舞台，本节课的实际教学就是采用测量法来加以验证的。学生操作：

第一组：画△ABC和△A₁B₁C₁，使∠A=∠A₁=45°，∠B=∠B₁=30°

第二组：画△ABC和△A₁B₁C₁，使∠A=∠A₁=60°，∠B=∠B₁=45°

分别测量∠C和∠C₁是否相等，测量三边长度，探求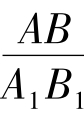、、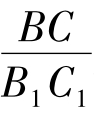是否相等。学生通过自己的测量，深信不疑的把脑中的问号拉成了感叹号。到此，学生已经成功的迈出了探索的第一步，也是意义最重大的一步。

在教学中，发现学生画图的速度很慢，甚至有的同学量出的角是不相等的，这就需要在平时加强对学生动手能力的培养。

（三）正确应用

学习数学的最终目的是应用，应用可以分两种：一种是解决数学内部的问题；另一种是解决生活实际问题。对照本节课，是数学内部的应用。传统教学对于解题能力的培养很有好处，在此我也吸收了一些很好的经验。同时，对本节课例题的选择又有很强的灵活性。比如动点在何处时三角形相似，再比如最后的“观察”中找相似三角形。

学生在这里基本都能理解解题的方法，但通过个别同学的板书，可以发现学生解题的规范性太差。这需要在今后的教学中吸取传统教学的优势，加强解题规范性的训练。

通过以上三个步骤，学生经历了“如果一个三角形的两角与另一个三角形的两角对应相等，那么这两个三角形相似”这一知识的形成过程，从而对该知识有了更为立体的认识。在这过程中，学生感受到了数学研究的一般方法。