数列通项求法小结

数列通项求法小结

杜晓红

（西安市庆安中学，陕西　西安　710077）

【摘要】本文提出了数学教学中常见的数列求通项问题，已知数列的递推关系式求数列通项。引入了构造法：通过构造新的等差、等比数列解决这类非等差、非等比的通项问题。构造法的引入对于学生解决非特殊数列通项有很好的导向作用。

【关键词】数列通项　构造法　累加　累乘　特征根方程

我们知道在数列问题中，数列通项是我们解决数列问题的关键。除了我们熟知的等差和等比数列通项以外，经常会遇到非等差和非等比数列的求通项问题。

知数列的递推关系式求通项是一种常见题型，那么构造法就成为我们解决这一类问题的一个很好的途径。

构造法就是在解决某些数学问题的过程中，通过对条件与结论的充分剖析，有时会联想出一种适当的辅助模型，以此促成命题转换，产生新的解题方法，这种思维方法的特点就是“构造”。若已知条件给的是数列的递推公式，而要求出该数列的通项公式，但使用构造法往往给人耳目一新的感觉.

本文是我根据教学中的具体实例以及教学参考资料将数列求通项的方法做一总结，希望方便于学生学习和老师的教学，主要有以下几类。

一、构造特殊数列

由于等差数列与等比数列的通项公式显然，对于一些递推数列问题，若能构造等差数列或等比数列，无疑是一种行之有效的构造方法.

例1：设各项均为正数的数列{a_n}的前n项和为S_n，对于任意正整数n，都有等式：+2a_n=4S_n成立，求{a_n}的通项a_n.

解：∵

（a_n+a_n－1）（a_n－a_n－1－2）=0，∵a_n+a_n－1≠0，∴a_n－a_n－1=2.

即{a_n}是以2为公差的等差数列，且.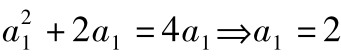

∴a_n=2+2（n－1）=2n

例2数列{a_n}中前n项的和S_n=2n－a_n，求数列的通项公式a_n.

解：∵a₁=S₁=2－a₁→a₁=1

当n≥2时，a_n=S_n－S_n－1=2n－a_n－［2（n－1）－a_n－1］=－a_n+2+a_n－1

令b_n=a_n－2，则b_n=b_n－1，且b₁=1－2=1

{b_n}是以为公比的等比数列，b_n=

∴a_n=2－（）^n－1.

二、a_n+1=a_n+f（n）型数列，（其中f_（n）不是常值函数）

此类数列解决的办法是累加法，具体做法是将通项变形为a_n+1－a_n=f（n），从而就有a₂－a₁=f（1），a₃－a₂=f（2），…，a_n－a_n－1=f（n－1）。将上述n－1个式子累加，变成a_n－a₁=f（1）+f（2）+…+f（n－1），进而求解。

例1在数列{a_n}中，a₁=2，a_n+1=a_n+2n－1，求a_n。

解：依题意有a₂－a₁=1，a₃－a₂=3，…，a_n－a_n－1=2n－3

逐项累加有a_n－a₁=1+3+…+2n－3==（n－1）²=n²－2n+1，从而a_n=n²－2n+3。

注：在运用累加法时，要特别注意项数，计算时项数容易出错。

类似题型练习：已知{a_n}满足a₁=1，a_n+1－a_n=求{a_n}的通项公式。

三、a_n+1=a_n·f（n）型数列，（其中f_（n）不是常值函数）

此类数列解决的办法是累积法，具体做法是将通项变形为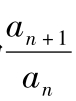=f（n），从而就有=f（1），=f（2），…，=f（n－1）将上述n－1个式子累乘，变成=f（1）·f（2）…f（n－1），进而求解。

例1已知数列{a_n}中a₁= 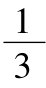，a_n=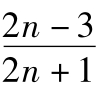·a_n－1（n≥2），求数列{a_n}的通项公式。

解：当时n≥2时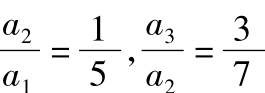，，，…，，将这n－1个式子累乘，得到，从而，当n=1时，，所以。

注：在运用累乘法时，还是要特别注意项数，计算时项数容易出错。

类似题型练习：在数列{a_n}中，a_n＞0，a₁=2，，求a_n.

提示：依题意分解因式可得［（n+1）a_n+1－na_n］（a_n+1+a_n）=0，而a_n＞0，所以（n+1）a_n+1－na_n=0，即。

四、a_n+1=pa_n+q型数列

此类数列解决的办法是将其构造成一个新的等比数列，再利用等比数列的性质进行求解，构造的办法有两种：（1）待定系数法构造，设a_n+1+m=p（a_n+m），展开整理a_n+1=pa_n+pm－m，比较系数有pm－m=b，所以m=，所以是等比数列，公比为p，首项为。（2）用做差法直接构造，a_n+1=pa_n+q，a_n=pa_n+1+q，两式相减有a_n+1－a_n=p（a_n－a_n－1），所以a_n+1－a_n是公比为p的等比数列。

例1在数列{a_n}中，a₁=1，当n≥2时，有a_n=3a_n－1+2，求{a_n}的通项公式。

解法1：设a_n+m=3（a_n－1+m），即有a_n=3a_n－1+2m，对比a_n=3a_n－1+2，得m=1，于是得a_n+1=3（a_n－1+1），数列{a_n+1}是以a₁+1=2为首项，以3为公比的等比数列，所以有a_n=2·3^n－1－1。

解法2：由已知递推式，得a_n+1=3a_n+2，a_n=3a_n－1+2，（n≥2），上述两式相减，得a_n+1－a_n=3（a_n－a_n－1），因此，数列（a_n+1－a_n）是以a₂－a₁=4为首项，以3为公比的等比数列。所以a_n+1－a_n=4·3^n－1，即3a_n+2－a_n=4·3^n－1，所以a_n= 2·3^n－1－1。

类似题型练习：已知数列{a_n}满足a₁=1，a_n+1=2a_n+1（n∈N^*）求数列{a_n}的通项公式.

注：根据题设特征恰当地构造辅助数列，利用基本数列可简捷地求出通项公式.