小数魔术师之除法

第2课　小数魔术师之除法

数学故事

破译百宝箱密码

欢欢和乐乐接到了来自数学宝岛的请柬。

欢欢和乐乐高兴地踏上了旅途。他们走啊走，终于来到了除法湖。欢欢低头看了看自己和乐乐的船票，上面写着渡船的规定:按号登船。每张船票上有一个除法算式，求出的商就是要找的船号。于是两个人约好到数学岛上见面，就分别找自己的船号去了。

欢欢拿着197.6÷5.2的船票，他想:把除数和被除数同时乘10，算式就转化为1976÷52，按照整数除法法则，他很快求出了商是38。于是欢欢登上了他的38号船。

乐乐拿着13.5÷0.03的船票，他很快算出商是45，于是一口气跑到45号船边，可是船上已经坐满了人准备开航了。乐乐急得大声喊:“喂，等等我!”检票员一看他的船票说:“朋友，你的船号不是45号。”乐乐愣住了，“难道我算错了?”他仔细想了想:13.5÷0.03，可以把除数0.03扩大到它的100倍转化成整数3，同时被除数13.5也扩大到它的100倍，这个算式转化为1350÷3，商是450。

“哦，我明白了，我的船票是450号。”乐乐挠了挠脑袋，重新找到了自己的船号，顺利地登上了数学宝岛。

欢欢和乐乐在数学宝岛上见到了那个神秘的百宝箱。大家正悄悄议论说:“百宝箱上的密码是由3道难题组成，谁有办法在规定的10秒钟之内解决所有难题，谁就能打开它!”

欢欢、乐乐兄弟俩自告奋勇来帮大家破解密码题。他们在箱子上的红色按钮上一按，“滴”的一声响，第一道密码题出现了:“最大的三位数是0.3的多少倍?”

欢欢转了转眼珠，立刻说出答案是3330。他是这样想的:最大的三位数是999，999除以0.3的商是3330，所以它是0.3的3330倍。

“咔嚓”一声，密码锁解开啦!

乐乐迫不及待地按下了箱子上黄色的按钮，“滴”一声响过后，第二道密码题出现了:“被除数(0除外)扩大到它的100倍，除数不变，商会怎样变化?”

乐乐赶紧动起了脑筋，被除数扩大到它的100倍，而除数不变，它们的商应该也会扩大到原数的100倍。乐乐立刻报出了这个答案，因为他们不能耽误一点儿时间，离10秒钟的时限还差5秒了。

只听见又是“咔嚓”一声，第二道密码锁打开啦!

好极了，兄弟俩同时按下箱子上的蓝色按钮，最后一道密码题出现了:“一个数保留两位小数是4.98，那么这个数最小是多少?”

乐乐想了想问欢欢:“是不是4.979呀?”欢欢思考了一会儿说:“不对，题目问的是最小的数，我想四舍五入后得到4.98的小数有很多，但最小的应该是4.975。”话音刚落，“咔嚓”一声，最后一道密码锁解开了，人们发出一阵欢呼声，百宝箱打开了，里面有许多的数学知识和数学宝典，大家高兴极了，纷纷向欢欢和乐乐表示祝贺。

巧解趣题

奇妙的循环圈

欢欢和乐乐两兄弟打开百宝箱后，被邀请留在数学宝岛上做客。他们每天潜心钻研箱子里的数学宝典，收获可丰富啦。瞧，这一天，欢欢看到了这道题:

不计算，直接填得数。

1÷7=0.142857142857…

2÷7=0.285714285714…

3÷7=0.428571428571…

4÷7=_____________　　　　　　

5÷7=_____________　　　　　　

6÷7=_____________　　　　　　

欢欢通过观察发现了两个“秘密”:①每个商都是循环小数;②循环节的数字都是1，4，2，8，5，7。

乐乐说:“这算什么秘密，我觉得前面三个算式的商，6个循环数字的排列顺序根本不同，没什么规律嘛!”

可是，数学宝典教会他们要仔细寻找规律。很快，欢欢和乐乐发现了循环节的排列规律:把1，4，2，8，5，7这6个数字，写成一个按顺时针方向的循环圈。

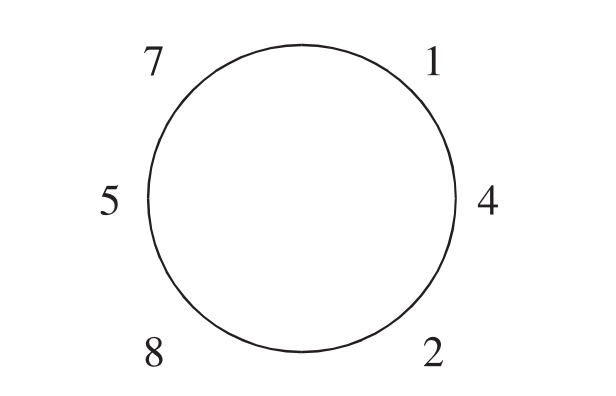
1÷7商的十分位是1，商的循环节就是142857;

2÷7商的十分位是2，商的循环节就是285714;

3÷7商的十分位是4，商的循环节就是428571;

……　　　　　　　　　　　　　　　　　　

解题思路:只要算准十分位上商几，就将它作为循环节的起点，按顺时针方向依次把这6个数字写下去。

聪明的同学们，有了这个奇妙的循环圈，请你们也来试一试，把下面的商直接写出来吧!

4÷7=_____________

5÷7=_____________

6÷7=_____________

智力提升

数学宝典里的知识还真不少呢，让我们趁这个机会进入“神秘的除法园地”，一块去体验吧!

1.“神机妙算”填一填。

(1)36分=(　)时　　　　　5980米=(　)千米

　　750千克=(　)吨　　　　　　　　　　

(2)两个因数的积是14，其中一个因数是2．8，另一个因数是(　)。

(3)6．4除以4．8的商用循环小数表示是(　)，这个商保留三位小数是(　)。

(4)在○里填上“＞”“＜”或“=”。

8．5÷0．9○8．5　　　　　　2．7÷2．7○1　　　　

4．8÷1．2○4．8　　　　　　6．56÷4．2○1　　　　

1．6÷0．05○1．6÷0．5　　9．2÷0．1○9．2×10

(5)求商的近似数时，要先看清(　)，除到比要保留的小数位数(　)，再按照(　)法求出近似数。

(6)4．976保留整数约是(　)，3．549精确到十分位约是(　)，10．6357省略百分位后面的尾数约是(　)。

(7)近似数是2．54的最大三位小数是(　)，最小的三位小数是(　)。

(8)根据商不变的规律填下面各数。

0．39÷0．25=(　)÷2．5

0．21÷0．6=(　)÷6　　

0．547÷1．5=(　)÷15　

0．8÷0．005=(　)÷5　　

(9)列竖式进行计算。

15．6÷3．5≈　　　　　　　　　　7．8÷16≈　

(得数保留一位小数)　　　　　　(得数保留两位小数)

80．5÷23=

(用乘法验算)

2.小小法官辨一辨。(对的打“√”，错的打“×”)。

(1)无限小数大于有限小数。　　　　　　　　(　)

(2)4．83÷0．7、48．3÷7和483÷70三个算式的商相等。　　　(　)

(3)在1．5353…，0．19292，5．314162…，8．4666…四个小数中，有三个循环小数。　　　　(　)

(4)一个数除以大于1的数，商一定大于这个数。　　　(　)

(5)无限小数就是循环小数。　　　　(　)

3.智多星来选一选。

(1)下面各式的结果大于1的算式是(　)。

A.0．99×1　　　B.1÷0．99　　　　C.0．99÷1

(2)下面算式中与3．07÷4．8结果相等的算式是(　)。

A.30．7÷48　　　B.30．7÷4．8　　　C.307÷48

(3)下面的数是循环小数的是(　)。

A.0．7777　　　B.15．438438438　　　　C.1．7474……

(4)对3．38585……这个小数，下面说法错误的是(　)。

A.是有限小数　　　　B.是无限小数　　　　C.是循环小数

(5)下面商最大的算式是(　)。

A.8．5÷0．125　　　B.8．5÷12．5　　　C.8．5÷1．25

4.探究规律算一算。

(1)用计算器计算，写出结果，并找出规律。

111111111÷9=　　　　　222222222÷18=

333333333÷27=　　　　　555555555÷45=

888888888÷72=　　　　　　　　　　　　

你发现了什么?说一说。根据你的发现，你还能写出一个与上面得数相等的除法算式吗?

(2)用计算器计算前四个算式的商，再试着写出后面两个算式的商。

3×7=　　　　　　　　3．3×6．7=　　　　

3．33×66．7=　　　　3．333×666．7=　　

3．3333×6666．7=　　3．33333×66666．7=

(3)用计算器计算前3题，再直接写出后6题的得数。

1234．5678×9=　　　　　1234．5678×18=

1234．5678×27=　　　　　1234．5678×36=

1234．5678×45=　　　　　1234．5678×54=

1234．5678×63=　　　　　1234．5678×72=

1234．5678×81=

(4)不计算，运用规律直接写出得数。

6×7=42　　　　　　　　　6．6×6．7=44．22

6．66×66．7=　　　　　　6．666×666．7=　

6．6666×6666．7=　　　　　　　　　　　　

5.解决生活中的数学问题。

(1)小洋原来有18．4元，爸爸又给了他7．2元，小洋用这些钱买了4支钢笔，每支钢笔多少元?

(2)工程队修一条公路，原计划每天修路1．65千米，20天可以完成。实际只用了15天，实际平均每天修路多少千米?

(3)有830千克的苹果要装纸箱运走，每个纸箱最多能装18千克，至少需要多少个纸箱才能全部运走?

(4)编一个中国结要用丝带1．7米，一卷长8米的丝带最多可以编几个这样的中国结?

(5)玩具厂购买一批布，原来做一个玩具熊需要0．8米，可以做720个。后来改进技术每个节约用布0．2米，这批布现在可以做多少个?

(6)一条高速公路长432千米，一辆客车4．5小时行完全程;一辆货车5．4小时行完全程。客车的速度比货车快多少?

(7)学校大门有一串彩灯，按“红、黄、绿、白”的规律排列起来，请你算一算，第18只和第24只彩灯分别是什么颜色?

(8)一个循环小数6.28732873…你知道它的小数点后面第70位上的数字是多少吗?

智慧阅读

《西游记》里的孙悟空是一个神通广大，本领高超的人物。他能七十二变:变虫、变树、变房子，还会腾云驾雾，一个筋斗可翻出十万八千里，但不管他怎样变幻，总还是落在如来佛的掌心里逃脱不掉。数学家们发现，这样的现象竟然也会在数字的变幻中出现，就让我们一起来探究一下吧!

神秘的“黑洞数”

黑洞数又称陷阱数，它们是一类具有奇特转换特性的整数。任何一个数字不全相同的整数，经有限“重排求差”操作，总会得某一个或一些数，这些数即为黑洞数。“重排求差”操作即组成该数的数字重排后得到的最大数减去重排后得到的最小数。

举个例子，随便找个数，如297，三个位上的数按从大到小和从小到大的顺序各排一次，得到972和279，相减972－279=693，按上面做法再做一次，得到594，再做一次，得到495。之后反复都得到495。

因此，三位数的黑洞数为495。

那么，四位数的黑洞数是什么呢?再来试试吧!

随便选一个四位数，如1628，先把四个位上的数按从大到小和从小到大的顺序各排一次，得到8621和1268，相减8621－1268=7353，再把7353按上面的方法做一遍，由大到小排列得7533，由小到大排列得3357，相减7533－3357=4176，把4176再重复一遍:7641－1467=6174。

如果再往下做，奇迹就出现了!7641－1467=6174，又回到6174。

这是偶然的吗?我们再随便举一个数，例如，开始时我们取数8208，重新排列后最大数为8820，最小数为0288，8820－288=8532;对8532重复以上过程:8532－2358=6174。这里，经过两步变换就掉入6174这个“陷阱”。

需要略加说明的是:以0开头的数，例如0288也得看成一个四位数。再如，我们开始取数2187，按要求进行变换:

2187→8721－1278=7443→7443－3447=3996→9963－3699=6264→6642－2466=4176→7641－1467=6174。

这里，经过五步变换就掉入了“陷阱”——6174。

拿6174本身来试，只需一步:7641－1467=6174，就掉入“陷阱”再也出不来了。

好啦!6174的“幽灵”又出现了，大家不妨试一试，对于任何一个数字(不完全相同的四位数)，最多运算7步，必然落入陷阱中。

同学们，数学中还有很多有趣、有意义的规律等着我们去探索和研究，让我们在数学中寻找更多的乐趣吧!1.想一想:“黑洞数”是怎么推导出来的?

2.试一试:下面数的“黑洞数”是多少?

请你以196尝试一下:第一步写出961－169，第二步之后变为(　)，再变为(　)，再变为(　)，再变为(　)，再变为(　)……所以这个数字游戏的“黑洞数”是(　)。

3.你还知道哪些“黑洞数”?

开心数学园

分苹果

小新家里来了5位同学。小新的妈妈想用苹果来招待这6位小朋友，可是家里只有5个苹果。怎么办呢?只好把苹果切开了，可是又不能切成碎块，小新的妈妈希望每个苹果最多切成3块。这就成了又一道题目:给6个孩子平均分配5个苹果，每个苹果都不许切成3块以上。小新的妈妈是怎样做的呢?