高斯的启示

第十一章　常识性思维游戏

所谓常识，即普通的知识、一般的知识、众所周知的知识。一是指与生俱来、无须特别学习的判断能力，或是众人皆知、无须解释或加以论证的知识；另一意思是指对一个理性的人来说是合理的知识，即“日常知识”。常识性思维游戏，也就是根据常识便可解决的游戏。生活大于一切，一个有常识的人，才是一个健全的人。

一点也不害怕

阿凡提被财主的手下抓了起来。财主将阿凡提绑在水池的柱子上，接着又将很多大冰块放在水面上。这个时候，水面刚好将阿凡提的脖子淹到。财主希望等冰块融化之后，可以将阿凡提淹死，然而阿凡提却一点也不害怕。

请问：冰块融化之后，水面会升高吗？

【妙趣解析】

由于冰块融化成水的体积，刚好等于它排开水的体积，所以水面一点都不会升高。

生日蛋糕

今天是明明的10岁生日，爸爸为他买了一个非常大的圆形蛋糕。然而即便是明明的生日，爸爸仍旧想考一下他。爸爸对明明说：“倘若你可以将这块蛋糕分成完全一样的两份，不光重量相同，形状也要一样，并且分出来的形状一定全部都是由曲线组成的，不可以出现直线段，如果你成功了，那么我会再奖励你一份礼物。”明明看着蛋糕，望了半天还是没有动手，你可以帮帮他吗？

【妙趣解析】

只要将蛋糕分成“太极图”的形式，就可以达到爸爸的要求了。

顽童的把戏

有一个小顽童，他最喜欢做一些自以为聪明的小把戏，经常将大人们逗得乐翻了天。有一次，小顽童弄出了这样一个把戏：将一根杠杆放在一只睡着的小猫的背上，将一个足球放在杠杆的左边，然后将一支正在燃烧的蜡烛放在杠杆的右边，这个时候，杠杆正好处于平衡状态，既没有动一下，也没有翻一下身。

请问：足球将滚向左边还是右边？

【妙趣解析】

蜡烛燃烧完了之后，质量会大大减少，杠杆会向左边倾斜，因此足球会滚向左边。

学习时间

有一个人常常抱怨没有学习时间。某次，他又对一个熟人说：“你知道吗？我的时间太紧了，以至于我根本腾不出学习的时间。你算一下，每天我都要睡8个小时，这样一来，一年的睡眠时间就是122天。寒假和暑假加起来，又是60天。每个星期六和星期日，我们都会接连休息两天，这样一年又要休息104天。每天的一日三餐，我都要花上3个小时，那么一年就需要46天。我每天在学校与家之间往返一共需要2个小时，这些时间加起来又是30天。你看看，所有的这些加起来有362天了。”他停了一下说：“我一年只有3天的学习时间，这样又怎么可能有好的成绩呢？”

请问：这个人究竟是在什么地方出错了？

【妙趣解析】

这个人在计算时间的时候重复计算了很多时间，比如说假期中的睡眠时间和吃饭时间，双休中的睡眠和吃饭时间，以及很多上学时走路的时间。

珍珠项链

警察甲、乙刚接手了一起谋杀案。一个寡妇在梳妆台前死去了，头部被硬物击破，基本上没找到什么线索。

甲说：“你注意到了吗？在死者的手中，有一串珍珠项链。”

乙说：“人是在梳妆台前死的，她正在梳妆打扮，这个时候被人害死，手上抓着项链也不奇怪。”

甲说：“错了，在死者的脖子上，早已经戴了项链，她不会再戴了。”

乙说：“说得很对，也许凶手也是一个女人，在搏斗的过程中，死者揪下了凶手脖子上的项链。”

甲说：“又错了，项链完整无缺。我认为这是死者的一种暗示，这个项链一定和凶手有关。”

乙说：“凶手？刚才邻居不是说过了嘛！这个女人不是信佛，就是讲道，平时接触的只有两种人，一是和尚，二是算命的，他们谁会戴项链呢？”

甲说：“谁戴……我似乎知道了。”

请问：凶手到底是什么人？

【妙趣解析】

死者手中抓着珍珠项链，暗示是和尚杀了她。因为和尚总是戴着珠串的，而算命的不会戴这些东西。

冤枉小狗

雷克家养了一条小狗，一天小狗自己跑出去玩，不多时，一位女士敲响了门，这位女士气愤地问：“你家养了一只狗吧，好好管教一下，它把我咬伤了，你说怎么办？”雷克看着女士浑身都好好的，笑着问：“我怎么没有看到咬伤的部位呢？”这时，这位女士卷起裤腿，只见白皙的小腿上，有红色的齿印，雷克看了一眼：“这绝对不是我家狗咬伤的。”看着愤怒依旧的女士，雷克又补充了依据，这位女士顿时没了气焰。你知道雷克说了一句什么话吗？

【妙趣解析】

雷克说：“我家狗不可能让你卷起裤腿然后下嘴咬，它没有那么聪明。”

寿星的年龄

200多年之前，更具体一点来说，在清代乾隆五十年的时候，乾隆皇帝在乾清宫举行了一次千叟宴，应邀参加宴会的老年人有3 900多位，其中有一个客人的年纪大得让人叹为观止。

那么，这位年龄非常大的老寿星的岁数到底有多大呢？乾隆皇帝对众人说了，但是并非明说，而是将一道对联的上联说了出来：花甲重开，外加三七岁月。

这个时候，当朝大臣纪晓岚正在一旁看热闹，对于那位老寿星的岁数，他也说出了自己的见解，当然也并非明说，而是将下联对了出来：古稀双庆，又多一个春秋。

请问：对联里面究竟说了些什么呢？这个老年人的岁数到底是多少呢？

【妙趣解析】

首先分析上联。所谓花甲，就是甲子的意思，一个甲子的时间为60年。“花甲重开”，则意味着已经度过了两个甲子，即120年。当然，这还不是真实的年龄，还得“外加三七岁月”，3与7相乘得21（年），因此总数为60×2＋3×7＝141（岁）。由此可见，乾隆皇帝说的是这个老人家的年龄有141岁。

其次再分析下联。所谓古稀，也就是70岁的意思。唐朝大诗人杜甫在诗歌《曲江二首》中说，“人生七十古来稀”。当然，由于现今我们的生活条件与医疗条件都好了很多，七十自称小弟弟，活到八十不稀奇，但是还在半个世纪之前，可以活到70岁，还是非常让人惊叹和令人羡慕的，通常都会大大地庆贺一番。“古稀双庆”，意思是说这个老先生经过了两次庆贺古稀，也就是过了两个70年，并且还不止于此，还“又多一个春秋”，总数为70×2＋1＝141（年）。由此可见，纪晓岚是在变个花样说那个老年人的年龄，也是141岁。

怪题巧解

第一部俄文数学动脑筋题目文集的作者是大诗人贝涅吉克托夫，对此，绝大多数俄国文学爱好者都持肯定态度。这本集子是以手稿的形式留存下来的，当初并没有被出版社刊印发行。1924年，人们发现了这份手稿，结果便引起了学术界和文学界的轰动。下面说一下诗人贝涅吉克托夫以小说的形式写成的一道题目，题目的原名为“怪题巧解”。

某妇人叫她的三个女儿去市场出售她的90个鸡蛋。对于最聪明的大女儿，她给了10个鸡蛋；对于二女儿，她给了30个鸡蛋；对于小女儿，她给了50个鸡蛋。然后妇人便对三个女儿说：你们先把售价商量好，之后便不再让步。你们都必须坚持同样的价钱，然而我又希望，我的大女儿可以运用她的智慧，纵然是根据你们共同商定的价钱，依旧可以将她自己手中那10个鸡蛋卖出二姑娘卖掉她那30个鸡蛋的钱，并教会二姑娘将她那30个鸡蛋卖出三姑娘那50个鸡蛋卖出的钱，并且还要让三个人的进项也一样。还有，我希望你们在卖蛋的时候，根据统计，不可低于每10个蛋10分钱，全部90个鸡蛋不可低于90分，也就是说不可低于30阿尔登（货币名）。

请问：三位姑娘如何才能完成她们的任务？

【妙趣解析】

三位姑娘在去市场的路上，一边走一边商量。之后，二姑娘、三姑娘都让大姐出一个好主意，大姐思考了一会儿，便说：“妹妹们，在以前，我们都是10个蛋10个蛋来卖的，这次我们不这么干，改为7个蛋7个蛋出售。每一份7个蛋，我们先给每一份订一个价钱，而妈妈的嘱咐，我们三个人也都可以遵守。一定要做到，一分钱也不要让！每份卖一个阿尔登，也就是3分，你们的意见如何？”

二姑娘说：“那太便宜了！”

三姑娘则问：“那么，剩下的那几个蛋应该卖什么价钱呢？”

大姑娘答道：“每个蛋卖3个阿尔登，买主如果等蛋下锅，一定会出这个价钱的。”

最后大家都同意了。

三姑娘的50个鸡蛋做成七份出售，结果一下就被抢光了，总共卖了7个阿尔登，最后筐子里面只剩下了1个鸡蛋。二姑娘的30个鸡蛋则做成四份出售，分别卖给了四个顾客，最后筐子里面只剩下了2个鸡蛋，总共卖了4个阿尔登。大姐则出售了一份7个的蛋，赚了1个阿尔登，最后筐子里面还剩下3个蛋。

这个时候，一个女厨师来到了市场上，她给大姑娘付了9个阿尔登，买下了她的3个鸡蛋。这样一来，加上前面卖出的1个阿尔登，大姑娘总共赚了10个阿尔登。二姑娘的2个鸡蛋换来了6个阿尔登，加上前面卖四份鸡蛋的4个阿尔登，总共赚了10个阿尔登。三姑娘剩下的1个蛋换来了3个阿尔登，连同以前卖七份鸡蛋的7个阿尔登，总共赚了10个阿尔登。

了不起的妙算

在中国古代的民间，“鸡兔同笼”的算题与算法曾经一度广为流传过，甚至被抬高为“了不起的妙算”。李汝珍是清代著名小说家，在小说《镜花缘》中，就写到过“鸡兔同笼”的算题和算法。

《镜花缘》中的故事是这样的：有一个才女，名叫米兰芬。有一次，米兰芬来到了一个阔人的家里，主人请她观赏楼下大厅里面的大小灯球，这些大小灯球啊，真是五彩缤纷，高低错落，宛若群星！

主人对米兰芬说：“楼下大厅里的灯可以分为两种，一种是灯下有一个大球，下面缀有两个小球；另一种是灯下有一个大球，下面缀有四个小球。楼下的大灯球总共有360个，小灯球总共有1 200个。”

最后，主人让米兰芬算一下两种灯球分别有多少个。

请问：你可以算出来吗？

【妙趣解析】

一个大灯球下缀两个小灯球，我们可以把它当成鸡；一个大灯球下缀有四个小灯球，我们可以把它当成兔。（360×4－1 200）/（4－2）＝240/2＝120（一大二小灯的盏数）；360－120＝240（一大四小灯的盏数）。

韩信分油

韩信是楚汉争霸时代一位非常有名的大将，他辅助刘邦成功消灭了楚霸王项羽，一手把汉朝的基业奠定了下来。在民间，流传着很多关于韩信的故事，其中不乏以韩信为主角的有关聪明人的故事，下面就是一例。

有一天，韩信骑着马走在大街上，看到两个人站在路边，正在为分油的事而发愁。在这两个人的中间有一只篓子，其容量为10斤，篓子中装满了油。此外，还有一只罐和一只葫芦，两样都是空的，罐可以装入7斤油，葫芦可以装入3斤油。两个人想平分这中间的10斤油，每个人各得5斤。然而都没有把秤带过来，只可以借用手头的三个容器，可以倒过来倒过去。应该如何分呢？

韩信骑在马背上，把情况了解之后，便对两个人说道：“葫芦归罐罐归篓，二人分油回家走。”说完之后，便打了一下马的屁股，扬长而去。两个人根据韩信所说的办法一会儿倒过来，一会儿倒过去，最后终于将油平均分成了两份，每人各得5斤。两个人都舒了一口气，高高兴兴地回家去了。

请问：他们到底是如何倒来倒去的呢？

【妙趣解析】

三种容器各自装油斤数的变化过程，可以从下面的数据看出：

篓10　7　7　4　4　1　1　8　8　5　5

罐0　0　3　3　6　6　7　0　2　2　5

葫芦0　3　0　3　0　3　2　2　0　3　0

韩信口中的“葫芦归罐”，意思是说将葫芦里面的油往罐里倒；“罐归篓”的意思则是将罐里的油向篓里倒。一般分油都会将油从大容器往小容器里面倒，现在却是将小容器里面的油向大容器里面“归”。将油倒进油葫芦里面，只可以得到3斤的油量；将葫芦里面的油向罐里“归”，“归”到第三次的时候，葫芦里面就只剩下2斤的油量了。再将满满的一罐油“归”进篓中，把空腾出来，将葫芦里面的2斤油“归”到空罐里面；最后再把一葫芦3斤油“归”到罐中，这样，分油的任务就完成了。

小人国

要说《格列佛游记》里面最有趣的故事，当数格列佛在小人国与大人国旅游了。小人国里面的一切物件，如人、畜、植物等的尺寸都只有正常人类的1／12。而大人国则刚好相反，全部物件的尺寸都是正常人类的12倍。作者为何会选12这一倍数，这是很容易理解的，因为英尺与英寸之间的倍数关系刚好是12，而作者则是地地道道的英国人。等于12倍或等于1／12，从表面看起来，这似乎不是很大的增减，然而在大人国和小人国里面，其自然环境与生活环境跟我们正常人类所熟悉的环境却有着非常大的差别，这种差别大大地超出了我们的意料，所以为我们提供了很多非常有趣的题目和材料。

格列佛在谈到小人国的情况时，这样说道：“为了将我送到首都去，他们给我派来了500匹健壮的马。”

再说一下小人国的牛羊。关于小人国的牛与羊，格列佛说当他离开时，只是随便地“将它们放入自己的衣袋里面。”

请问：这有没有可能？

【妙趣解析】

从题目我们可以知道，格列佛的体积是小人国人的1 728倍（12×12× 12）。同理，他的体重自然也是小人国人的1 728倍。想用小人国的马来搬运格列佛的身体，其难度相当于搬运1 728个健壮的小人国人。这样我们就可以理解，为什么搬运格列佛要用500匹健壮的马了。

小人国的牲畜的体重只是正常牲畜体重的1/1 758。我们的牛，通常都有1.5米高，体重则大约为400千克。这样可以推算出，小人国的牛，其身高只有12厘米，体重只有400／1 728千克，也就是说不够1／4千克。非常明显，小人国的牛就像玩具一般，如果愿意的话，是完全可以放进衣袋里面去的。

秘传的手稿

三国时代，刘备的军师诸葛亮，是一个博学多才、神机妙算的人。在罗贯中所著的古典长篇小说《三国演义》第104回里面，说到诸葛亮在出师和魏兵打仗的时候，身上患了重病，手下有一员大将姜维进入行军帐里面看望他。诸葛亮对他说道：“……吾平生所学，已著书二十四篇，计十万四千一百一十二字，内有八务、七戒、六恐、五惧之法。吾遍观诸将，无人可授，独汝可传我书。切勿轻忽！”

从这段话中，我们可以知道，诸葛亮秘传给姜维的手稿总共有24篇，104 112字。大略做一下估计，就可以推算出平均每篇大概有四千多字。

请问：你能不能知道每篇的平均字数是整数，还是非整数？

【妙趣解析】

解决这一问题，可以利用数的整除性判别法。由于24＝3×8，3与8互质，现在只要看总字数104 112可不可以同时被3与8整除。104 112的各位数字的和是1＋0＋4＋1＋1＋2＝9，9可以被3整除，因此104 112可以被3整除。

要看104 112可不可以被8整除，只需看它的末三位112可不可以被8整除。而112÷8＝14，由此可知，112是8的倍数，所以104 112也可以被8整除。因此104 112可以被24整除，也就是说，诸葛亮每篇手稿的平均字数是整数。

事实上，使用除法，就可以直接算出诸葛亮每篇手稿的平均字数为104 112÷24＝4 338。

分牲口

有一位大牧场主住在美国西部，他自知自己已经上了年纪，因此有一天，他将所有的儿子都召集在了一起，并对他们说，要在自己的有生之年，趁还有时间，将自己的牲口分给他们。

大牧场主首先对大儿子约翰说：“你认为你能饲养多少头奶牛，那么你就可以拿走多少头奶牛。你的老婆南希则可以将剩下奶牛的九分之一取走。”

他又对第二个儿子萨姆说：“你不仅可以拿走和约翰一样多的奶牛，而且还可以多获得一头，毕竟约翰已经有了先挑的机会。至于你的老婆萨莉，我会将剩下奶牛的九分之一送给她。”

对第三个儿子，大牧场主说了和上面一样的话。第三个儿子能够拿到的奶牛将比第二个儿子多一头，而其老婆也会拿到剩下奶牛的九分之一。对于其他儿子，这样的话也照样适用：和其年龄稍大的兄长所得的奶牛数相比，每人拿到的奶牛数都会多出一头，而每个儿子的老婆则可以拿到剩下来的奶牛的九分之一。

当最小的儿子将奶牛拿走之后，已经没有剩下的牛送给他的老婆了。于是大牧场主又说道：“马的价值是奶牛价值的两倍，我现在愿意将我所拥有的七匹马根据这样的原则分配，即每个家庭都可以分到相同价值的牲口。”

请问：大牧场主一共拥有多少头奶牛？他一共有多少个儿子？

【妙趣解析】

大牧场主一共有7个儿子，56头奶牛。大儿子拿了2头奶牛，他老婆拿了6头奶牛；第二个儿子拿了3头奶牛，他老婆拿了5头奶牛；第三个儿子拿了4头奶牛，他老婆也拿了4头奶牛。这样依次类推，直到最后，第七个儿子拿到8头奶牛，但是奶牛已经全部分光了，他的老婆已经无牛可分了。奇怪的是，现在每个家庭都分到了8头奶牛，因此每家可以再分到1匹马。这样一来，7个儿子都分到了价值相等的牲口。

屋顶上有积雪

有一天，警察局接到一个报警电话，有一家人被谋杀了，经过仔细排查后，最终锁定了犯罪嫌疑人。因为这家人借了很多钱给这个人，但是因为有急事，所以最近催促其赶紧还钱，因此这个人有理由痛下杀手。当询问这个人时，他称：“昨天发生命案的时间，我正好在家，因为很疲倦，所以，我烧水洗澡，并且洗了一些衣服。”警长看着屋顶堆着的积雪，然后严肃地对他说：“你最好老实交代你的罪行。”

请问：警长是如何发现异常的？

【妙趣解析】

因为警长看到他家屋顶有厚厚的积雪，但是他却说自己昨晚烧过热水，如果是这样，那么烟囱附近的积雪不会那么厚，它们应该早就被蒸气融化了，所以，警长判断这个人在说谎。

999文钱

下面这道算术题是用歌谣形式写成的：九百九十九文钱，甜果苦果买一千。四文钱买苦果七，十一文钱九个甜。甜苦两果各几个？请君布算莫迟延！在用词上，这首歌谣的确有一点儿老古董的味道，而且用的钱也并非现在的人民币。这道题目载于中国古代数学书《算法统宗》中。《算法统宗》是在1592年刻印的，作者名叫程大位，生于公元1533年，死于公元1606年，是明代著名的数学家。

这首歌谣的意思是这样的：现有999文钱，买一种甜果与一种苦果，两种水果一共买了1 000只。其中苦果的价钱是4文钱可以买7只，甜果的价钱是11文钱可以买9只。

请问：999文钱一共买了多少只甜果，多少只苦果？

【妙趣解析】

我们可以先假定1 000只买的全是甜果，由于每9只甜果需要付11文钱，因此买1 000只甜果，需要付的钱数为：11/9×1 000＝11 000/9（文）。

甜果比较贵，苦果相对便宜一些，全买甜果多花的钱为：11 000/9－999 ＝2 009/9（文）。

要想将多花的这些钱省下来，就必须拿出一部分甜果将同样个数的苦果换过来。每拿一只甜果换回一只苦果，节省的钱数为：11/9－4/7＝41/63（文）。

因此需要换回的苦果只数为：2 009／9÷41／63＝2 009/9×63/41＝343。

还剩下的甜果只数为：1 000－343＝657。

所以999文钱一共买了657只甜果，343只苦果。这个时候，买甜果的钱为803文，买苦果的钱为196文，加起来刚好是999文。

一群羊

这道题目也来源于《算法统宗》。原题的编写，主要是通过诗的形式，虽然有些文言化，但还是挺生动有趣的，现抄录如下：甲赶群羊逐草茂，乙拽肥羊一只随其后，戏问甲及一百否？甲云所说无差谬，若得这般一群凑，再添半群小半群，得你一只来方凑，玄机奥妙谁参透？

题目大概的意思是这样的：有一个牧羊人甲赶着一群羊，来到了一片青草茂盛的地方。另外还有一个牧羊人乙，手中牵着一只肥羊跟在牧羊人甲的后面。乙走上前，对甲开玩笑似地说：“你的羊满一百只了吗？”甲答道：“满一百只了，不过有一个前提，就是先往我这群羊里再添进同样多的一群羊，接着再添进半群的四分之一群，然后再将你的这一只也添进去，这样就可以凑满一百了。”

请问：这群羊到底有多少只呢？

【妙趣解析】

倘若不加进乙的一只肥羊，那么总数只有99只，而且这个时候的总数等于羊群原来只数的一倍、再加一倍、再加二分之一倍和四分之一倍，因此这群羊的只数是：99÷（1＋1＋1／2＋1／4）＝36，即这群羊总共有36只。

滚球游戏

古时候的丹麦，存在着一种滚球游戏，据说现在的保龄球，即是由它演变而来的。在玩这种游戏的时候，需要把13根木柱在地上竖成一行，接着用一只球对其中一根木柱或相邻的两根木柱进行猛击。因为击球者和木柱之间距离非常近，所以玩这种游戏根本就不需什么超凡的技巧，即便是随心所欲，也可以将任意一根木柱或相邻的两根木柱击倒。两个比赛者轮流击球，哪个人将最后一根木柱击倒，那么他就是最终的赢家。

与瑞普比赛的是一个游戏老手，他刚刚将第2号木柱击倒了。瑞普或者是将剩下12根木柱中的一根击倒，或者是将球往10个空之中的任意一个投去，这样就可以一次同时将两根相邻的木柱子击倒了。为了保证这一局能够获得胜利，瑞普应该如何做才对呢？而瑞普的对手如果想获胜，他开始的时候，第一个应将哪根木柱击倒呢？

【妙趣解析】

瑞普可以选择将第6号或者第10号木柱击倒。这样一来，木柱就会被分成1根、3根、7根，此后，不管瑞普的对手施展什么伎俩，只要瑞普能够采取正确的战略，那么对手就一定会输。而瑞普的对手要想获取胜利，那么在开始的时候，他应该将第7号木柱击倒，这样就可以将木柱分成各有6根木柱的两组了。接下来，不管瑞普将哪一个组里的木柱投掷出去，瑞普的对手只要在另一组里重演瑞普的动作，那么就会获取最后的胜利。

中秋节

以前过中秋节是多么美好呵！爸爸躺在自己喜爱的椅子上吹着笛子，妈妈与孩子们则一起吃月饼，而对其中3个孩子而言，这一天更是不比寻常。因为中秋节是他们的生日。根据以下条件，看你能否推断出他们的年龄：

（1）今天小华的年龄是小明和小超年龄相加的总和。

（2）去年中秋节时，小明的年龄是小超的2倍。

（3）倘若从现在算起，那么两年之后，小华是小超的2倍。

请问：小华、小明和小超各自的年龄是多少？

【妙趣解析】

在中秋节这一天，小华是8岁，小明是5岁，小超是3岁。

炮舰外交

普左罗总统刚刚得到了一支舰队的支援，这样更有把握保卫他的岛国。这只新舰队是由两艘霍萨级炮舰组成的，火力巨大，然而美中不足的是，这两艘霍萨级炮舰消耗燃料非常厉害，而炮舰上装的木柴只能够让锅炉烧24小时，也就是说，炮舰只可以航行120英里。

普左罗为了炫耀自己最好的军舰，打算进行一次盛大的环岛航行。然而，海军大臣却提醒普左罗，该岛的周长要大于120英里。对于普左罗而言，这次航行关乎自己的荣誉，而对海军大臣来说，却是一个令人头疼的问题。

但是，经过本地大学的数学教授与巫师的计算，认为倘若在海上用一艘舰为另一艘舰装运燃料的话，那么环岛航行还是能够完成的。虽然在港内给一艘炮舰装燃料需要花费8小时，可是在海上，这艘装燃料的炮舰却无须停船等它的姐妹舰赶上来。只是一艘舰在海上往另一艘舰转运燃料的时候，才会稍稍耽误一下普左罗庄严的航行。倘若这个小岛再大那么一点儿，那么整个航行就会成为泡影。

请问：小岛的周长到底是多少？

【妙趣解析】

普左罗岛国的周长为200英里。两艘舰同一时间出发，航行40英里之后，护航舰把它余下的燃料的一半转运到旗舰上去，之后再返回港口。护航舰把燃料重新装好之后，再从相反的方向往快要耗尽燃料的旗舰开去。这个时候旗舰距离港口还剩下40英里。护航舰把自己剩下的燃料的一半又一次转运到旗舰上去，接着，两艘舰再一起开往港口，抵达目的地的时候，两艘舰的燃料也刚好用完了。

丢番图的墓志铭

丢番图是古希腊的数学家，大概生活在公元246年至公元330年，距离现在已经有两千年左右了。在代数学的发展上面，丢番图做出过巨大的贡献。

丢番图写有一本书——《算术》，总共有十三卷。在这部书里面，收集了很多十分有趣的问题，每道题的解法都很巧妙，出人意料。这些解法不仅可以开动人的脑筋，而且还能启迪人的智慧，所以后人将这类题目称为丢番图问题。

然而，关于丢番图的生平，人们却知道得很少。在《希腊诗文集》中，我们可以找到关于他的唯一的简历。诗集中有一首关于丢番图的“墓志铭”，是用诗歌形式写成的，作者为麦特罗尔。这首“墓志铭”如下：

过路的人！

这儿埋葬着丢番图。

请计算下列数目，

便可知他一生经过了多少寒暑。

他一生的六分之一是幸福的童年，

十二分之一是无忧无虑的少年。

再过去七分之一的年程，

他建立了幸福的家庭。

五年后儿子出生，

不料儿子竟先其父四年而终，

只活到父亲岁数的一半。

晚年丧子老人真可怜，

悲痛之中度过了风烛残年。

请你算一算，丢番图活到多大，

才和死神见面？

请问：丢番图究竟活到了多少岁？

【妙趣解析】

在丢番图的墓志铭中，依次出现了1／6、1／12、1／7、1／2，这些都是以丢番图的年龄作为单位“1”的，所以，丢番图的年龄必定是这四个分数分母的公倍数。6、12、7、2的公倍数有84、168、252……丢番图无法活到168岁或更大的年龄，所以可以肯定，丢番图活到了84岁。

硬币

为了以备急用，张阿姨总是喜欢在家存放大笔的钱。唯一的问题就是，张阿姨从来不相信纸币，因此她存放的都是硬币。同时，她把自己的存款藏在窃贼最不可能想到的地方——盛汤的碗中。当张阿姨数钱的时候，她发现了一个非常巧的事情：她的1 500枚硬币刚好是800元，硬币分为1元硬币、5角硬币和1角硬币。

请问：这三种不同面值的硬币各有多少个？

【妙趣解析】

每种面值的硬币各有500枚，它们依次为：

500枚1元硬币＝500元；

500枚5角硬币＝250元；

500枚1角硬币＝50元。

流水问题

“小桥、流水、人家”，流水问题可以说是随处可见。在一本成书于公元10世纪左右欧洲的《希腊文集》中，就有一个关于流水的问题。题目是用诗的形式写成的：

这是一座独眼巨人铜像，

雕塑家技艺非凡。

铜像中巧设机关：

巨人的手、口、眼，

连接着大小水管。

藏在手中的管道，

三天将水池注满；

独眼中的水管需时一天；

口中吐出的水柱，

只需五分之二天。

三处同时放水，

请问：空池几天可以装满？

【妙趣解析】

从题意可知，铜像手中的水管单独开放，只需要3天时间，就可以将水池注满，因此1天可注入水池的1/3；铜像眼中的水管单独开放，1天刚好可以将水池注满；口中吐出的水柱1天可注入水池的5/2。

如果三处同时放水的话，只要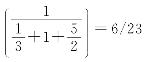天就可以将水池注满。

高斯的启示

高斯是德国大数学家，他小时候有一个故事，大家可能都很熟悉了。

据说在高斯十岁的时候，老师在黑板上写了一个题目：1＋2＋3＋……＋99＋100的和是多少？

老师刚刚将题目写完，小高斯就把答案算出来了：这100个数相加，和为5 050。

原来，小高斯的算法是这样的：依次将这100个数的头与尾加在起来，即1＋100，2＋99，3＋98，……，50＋51，一共有50对，每对皆为101，因此1至100的总和为101×50＝5 050。

现在，让你算一道题目：从1到1 000 000，这100万个数的数字之和为多少？

必须注意的是，这里所说的“100万个数的数字之和”，并非“这100万个数字之和”。比如说，1、2、3、4、5、6、7、8、9、10、11、12，这12个数字的个数之和为1＋2＋3＋4＋5＋6＋7＋8＋9＋1＋0＋1＋1＋1＋2＝51。

你可以认真想一下小高斯用的方法，这样会对你算这道题有很大的帮助。

【妙趣解析】

可以在这100万个数字前面加一个“0”，再将这些数字两两分组：999 999和0；999 998和1；999 997和2；999 996和3……依此类推，一共可以分成50万组，最后剩下1 000 000这个数不成对。各组数的数字之和都是9＋9＋9＋9＋9＋9＋9＝54，最后的1 000 000数字之和为1。因此这100万个数的数字之各为：（54×500 000）＋1＝27 000 001。

纵火犯

一天晚上，有一家发生火灾，因为火势太大，所以很多附近的房屋都受到了破坏，很多人损失惨重。经过调查发现，火灾是从小丽家蔓延开的，现场很多东西都被烧毁。当警察询问小丽是怎么一回事儿时，她称：“昨天，和丈夫、孩子参加婚礼，回来之后，孩子有些饿了，所以我就给他做东西，我听见孩子惊叫一下，赶紧冲出去，没想到，我忘记关煤气灶，火焰就把油锅燃了，这时我犯了一个错误，那就是把一桶油浇了上去，一下子整个厨房都着火了，我都没来得及通知丈夫和孩子。”一位警员看着小丽，对她冷冷地说：“不好意思，这位太太，你最好是和我们走一趟，因为你涉嫌故意纵火。”警察为什么这么说？

【妙趣解析】

因为水比油要重，如果油着火的话，用水灭的话，反而达不到效果，如果用油的话，那么燃烧的油肯定会因为缺氧而停止燃烧，但是小丽却说因为倒油，导致火势增大，这不符合常识，所以，很可能是故意纵火。

生鸡蛋和熟鸡蛋

欢欢的爸爸由于工作的需要，必须到外地出差，临行之前，欢欢的妈妈为他煮了几个鸡蛋。然而，欢欢一不小心，就将生鸡蛋与熟鸡蛋混在了一起。妈妈十分生气，命令欢欢将熟鸡蛋从生鸡蛋里面挑出来，不然的话就不可以吃晚饭。欢欢看了看这一堆的鸡蛋，陷入思考中：从外表上来看，根本分不出哪个是生鸡蛋，哪个是熟鸡蛋，倘若一个一个地打开，虽然可以分出来，但是会弄坏生鸡蛋。应该如何处理呢？

请问：你能帮欢欢想一想办法吗？否则的话，他就吃不了晚饭了。

【妙趣解析】

将鸡蛋一个一个地旋转起来，熟鸡蛋一般都容易转起来，而生鸡蛋则很难转起来。这主要是因为，在生鸡蛋里面，蛋清与蛋黄都呈液体形态，因此想让鸡蛋转起来，往往不太容易；然而当鸡蛋煮熟之后，蛋白与蛋黄就牢牢地“抱”成了一团，变成了一个整体，所以不难旋转起来。