为唤起学生的创新意识而教学

为唤起学生的创新意识而教学

高建斌

创造是人类社会赖以生存和发展的根基，它的作用随着社会的进步和科技的发展而增大，它的威力将在知识经济时代变得更加巨大和不可替代。而培养未来公民的创造能力离不开教育，离不开中小学教师创造性地工作。只有教师认识到培养学生创造意识和能力的重要性和可能性，并摒弃陈旧的教学思想观念，舍弃一些以浪费绝大多数学生智力资源为代价的急功近利的教学行为，才可能避免学生的一个想法、一个新点子和一个假说淹没在我们的教鞭之下；只有用艰苦创业的态度面对经济社会，全心全意地为培养学生的创新素质而创造性地施教，才可能真正为学生能自信地迎接新世纪的挑战做一点实事。下面我从数学教学方面谈一点唤起学生创新意识的想法和做法。

一、让学生好奇地问

兴趣是求知的动力，好奇又是兴趣的先导，是保证人们探索未知世纪最隐秘的动力，而好奇心是人的本能，人皆有之，只是强弱不同罢了。

在数学教学过程中，教师要重视和发展学生的好奇心，让每一个学生养成想问题、问问题、挖问题和延伸问题的习惯，尽量避免在严谨的数学演绎规则下形成“毛毛虫的爬行”习惯，让每一个学生知道自己有权利和能力提出新见解、发现新问题。这一点对学生的发展很重要，它有利于学生克服迷信和盲从，树立起科学的思想和方法，有利于学生形成良好的学习品质。教师要把培养学生旺盛的好奇心作为数学教学目标之一来完成，在教学中要学会耐心倾听学生提出的每一个问题，要努力克服自己在教学中的思维定势，绝不能因为学生问及的问题远离“高考”套路而谢绝解答。

比如，学习了集合后，学生S₁对A和B的交集A∩B={X|X∈A，且X∈B}产生疑问：“在A与B交集定义里面集合A和B应限定为非空集合，否则，若B是空集，则有A∩覫={X|X∈A，且X∈覫}，而‘X∈覫’表示X是覫的元素，这与空集中不含任何元素矛盾。”S1能在别人看不到问题的地方发现问题、提出问题，这种创造性思维的闪现，教师要加倍珍惜和爱护。教学中像这样的“生长点”可信手拈来。

如“指数函数”一节有一个例题：“一种放射性物质不断变化为其他物质，每经过一年剩留的质量约为原来的84%。画出这种物质的剩留量随时间变化的图像并从图像求出约经过多少年，剩留量是原来的一半。”学生S₂看完题立刻就问：“什么是放射性物质，这种变化是化学变化吗？”还有学生问：“这和冬天的冰块过一段时间变小一样吗？”对这些突如其来的问题，即使老师一时回答不准也不能以“离谱”太远为借口简单推托。像这样跨学科的问题若常受冷落，学生自然不知道数学在其中的作用，学生的好奇触觉也就停止发展，创造的火花就会熄灭。对这些多学科交叉的知识，我们要有意识地让学生了解，像此题目中涉及的核反应中的一些概念，与本题有直接联系的仅是放射性衰变定律（放射性元素衰变过程中，原子核数按指数规律随时间而减少）的数学表达式N=N₀e^-λ1（任何时间t=0时的原子核数目N，λ为衰变常数，N 0是t=0时的原子核数目），本题的指数函数为y=0.84^χ，用图像法求出此放射性物质的半衰期约为4年。如果在数学教学中能冲出为“考”而教学的束缚，像这样的“种瓜得豆”所带来的学生学习观念的更新和思考问题方法的变化，是非常有益的。这种灵活发现和灵活应变在科学研究中能创造意想不到的奇迹。

二、让学生自信地想和说

“自信人生二百年，会当水击三千里”，这是毛泽东人生态度的写照；“心想事成”、“梦想成真”常常作为人们相互勉励之语，这里“成功”的前提是先有“梦想”和“自信”。当代企业用“只有想不到，没有做不到”的豪迈语言来表明自信的思考、想象和创造是多么难得和重要。作为教师，要善待学生在学习过程中表现出来的“出格”和“瞎想“，鼓励学生自信地想和说。教学正余弦曲线时，为了让学生对这个像一根跳动的绳一样的图像有一个可信的感性认识，我给学生用物理中“演示简谐振动图像的装置”“画”图像，学生也参与实验和观察，可还没有待我向学生展示这个图像的神奇特点，突然一个学生说：“这有个啥，这‘图’我见多了，用手拎一桶水向前走（胳膊左右摆动）时，洒在地上的水就是这个样……我家的公牛边走边撒尿留下的也是这个样子……”班内哄堂大笑。这突如其来的场面使我有些失意，可细细琢磨觉得他说得有道理，不得已肯定了他的说法，并表扬了他留意身边问题的好习惯。后来这个学生对正余弦函数的单调性、周期性很有兴趣，并能形象地说出余弦曲线是“迟来”的正弦曲线。我想，如果我当时以不“文雅”伤害了他，那么不仅仅是损害了他的自尊，会将他学习数学的激情和求异冲动一起“焚烧”，这也会使其他学生再不敢“出格”，最终是学生们不可能再“出格”，创新的精神也就一同死去，这就变成教育的悲哀了。

在课堂教学中，哪怕学生的想法只是错误的“瞎想”，教师也要加倍爱护，因为“想”的过程比“结果”要珍贵得多。例如，学习球表面积公式时，我先帮助学生回忆了数学家刘微的“割圆术”，即用圆内接正多边形的面积S_N=1/2P_nr_n近似表示圆的面积，当圆内接正多边形的边数n无限增加时，r_n→R，P_n→2лR，Sn→S圆=лR²，让学生了解用极限方法进行推算的基本思想，启发学生寻找球面积的求法。学生S₃说“圆的面积能用圆内接正多边形无限逼近，球面的面积可用球内接正多面体的面积来逼近……”学生S₄说“有道理，如足球，旋转的反光灯……”学生S₅又说：“正多面体的表面积怎样求呢？”，等等。学生的思维从二维的圆和正多边形向三维的球和多面体方向发展，尽管他们走错了路（正多面体有且只有五种），但能用极限的思想进行合理的“瞎想”，这也是创新思维的闪现，教师需给学生作鼓励性的说明后，再启发学生从球面的形成过程来考虑，引导学生去发现，“割半圆→切球体”，最后到“割四分之一圆→切半球体”。这里如果没有老师的信任的鼓励，学生就会失去自信，就会自动关闭探索的动力系统。大多数学生从数学学习中只能学会模仿和“盗版”的技术，而这种“技能”在未来社会只能是高科技下的“小佣人”。因此，教师要利用好数学这场创新因素很多的天地，真正让学生在这块天地里自由自信地走一程。

三、让学生尽情地体验

毛泽东说：一切真知都是从直接经验发源的。在目前的课堂教学中老师应该且必须重视学生的直接经验对学习数学的正面影响，想尽一切办法为学生创造条件，让学生去感知、去体验、去发现，哪怕如同“2+3=3+2”这样很简单的问题，还是像“丈量土地”这样远古的问题，教师只有让学生在实践中激起学习数学的兴趣，在解决问题中唤起学习数学的热情，数学教与学的过程才会有创造激情和冲动，学生的视线方可穿破坚固的“围城”，学生的思想才能冲出定势的禁锢，学生的各种奇思妙想才能表露出来并得以完善和发展。

例如，小学生学习乘除法时，让学生参与操作实验：（1）每个盘子有2个苹果，3个盘子共有多少苹果？2+2+2=6或2×3=6；（2）6个苹果每人取2个，可分给几个人？（第一个人拿走2个后还剩4个，接着第二个人拿走2个后还剩2个，第三个人再拿走2个，正好分完）即6-2-2-2=0或6÷2=3。如果小学生对乘除法有这样深刻的体验，到初中学习乘方与开方运算时，就能用乘法“累加”来发展乘方的概念（如3×3×3×3＝3⁴）。同样在正整数集内实施除法时，当“除数”相同时，除法发展为开方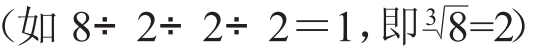（。这些有益的操作或实践，包含和孕育着儿童的天真和创造的幼芽，动一动、做一做、想一想，与高创造力者有相同的心理品质。

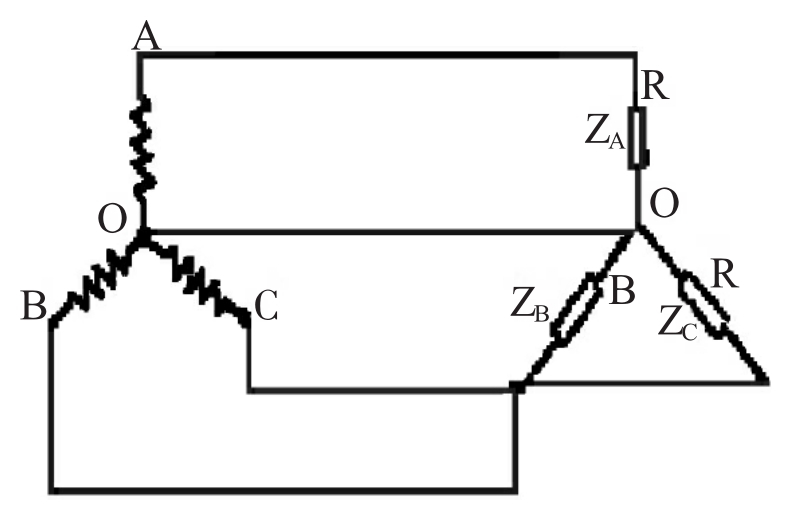
再如高中代数（上）一道题：“发电厂发出的电是三相交流电，它的三根导线上的电流强度分别是时间t的函数：IA=Isinωt，IB=Isin（ωt+120°），Ic=Isin（ωt+240°），求证：I_A+I_B+I_C=0。”这道三角题的证明是很简单的，可学生却问了一个“古怪”的问题，“I_A+I_B+I_C=0”是不是反映照明线路中的地线无电压和电流呢？这又是一个突如其来的难答问题，因为要讲清高中物理第二册“三相交变电流”中的问题不太容易，但我还是查阅资料给了学生一个了解性的回答，先简介物理（第二册）三相交变电流中星形连接、相线、中性线（或零线），再简介照明线路中中性线一般情况下不是无电流（如图）。

要让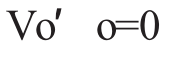则要负载Z_A=Z_B=Z_C，这时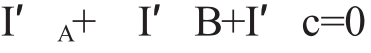零线上才无电流通过（如果这样，三相四线制供电线路就可去掉中性线（零线）变成三相三线制，他在工业上有广泛的应用）。但一般地照明线路是动态的用电过程，不可能做到Z_A=Z_B=Z_C，所以均为三相四线制供电，且I′A+I′B+I′c≠0，即零线（或地线）中也有电流，但不会使人感觉到（因为电压一般在10伏以下），可让学生去测验这一结果。这样回答学生的问题在有些人的眼里简直是“画蛇添足”、“离题万里”之举，就是同学科的老师也说这是不必要的浪费课堂教学时间，可我还是觉得这样做不仅能使这道数学和物理的诱惑力变大，对激发学生学习数学与物理题的兴趣有不可低估的作用。

以上提及的三个方面，意在呼唤同仁们以民族的复兴为着眼点，为培养学生的创造精神和创新意识进行创造性的工作，用我们创造性的教来唤起学生创造性的学，用我们创造性的思维方法锻炼学生的创造性思维品质，用敏锐的眼睛发现教材中的“点火处”，并帮助学生“再点火”。只有我们能换一双眼睛看问题，换一幅脑子思考问题，换一种方法解决问题，教与学才会合理地碰撞出创造的火花，我们的学生才会有标新立异的冲动，才会有创造思想和创新意识的萌芽和发展。

（载《人民教育》2000年第1期）