拼板的组合图形

第1章　J＇s拼板编号法及拼板组合图形

1．1　拼板的编号

为了认识区别各个不同形状的拼板，J＇s拼板编号法对12块拼板进行编号，如图1－1所示。

图1－1　J＇s拼板编号法

拼板的编号基本上采用象形法，将拼板的形状与阿拉伯数字联系在一起，相互对应，便于记忆。但其中8号拼板和10号拼板引用我国的数码计数的象形^[1]，12号拼板则象形英文字母L^[2]。从0到10，再加上英文字母L共12个代码，对应12块拼板，易于识别和记忆。

拼板有正面与反面，在拼图时允许拼板反摆，因此会出现拼板的正反。有些拼板的反面与正面是同样的，如1号拼板，反过来也是同样的形状；但也有不一样的，如2号拼板反过来就不同了。归纳起来，若拼板的形状具有轴对称的性质，则称为“偶拼板”（见图1－2），偶拼板正反面图形是相同的，如0号、1号、3号、8号、10号和L号拼板，计有6块。若拼板反面的形状与原图形是轴对称的，则称为“奇拼板”，奇拼板有2号、4号、5号、6号、7号和9号，也是6块。原拼板的对称拼板称为“拼板的反面”，在其编号上加“－”，如2号拼板的反面记作拼板 2号。图1－3中列出了奇拼板及其编号。

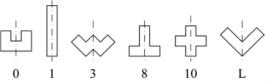
图1－2　偶拼板的轴对称图

在本书插图及图集中，偶拼板和奇拼板的正面采用纯色，奇拼板的反面饰以小圆点花纹。

在实际拼图中，偶拼板比较呆滞，奇拼板则显得活跃。

图1－3　具有正反面的奇拼板及其编号

1．2　拼板的演变与拼板间的关联

12块拼板虽然形状各不相同，但它们都能互相变化，有着一定的内在联系。了解各拼板的来龙去脉及它们相互演变过程，有助于“伤脑筋十二块”拼图和进行图形的变换。

每个拼板都是5个单位面积（格），拼板的演变就是拼板的格结构的变化。

1．2．1　拼板的分类

根据拼板形状外框可以分成4种，如表1－1所示。前3类拼板的周长等于其图形外框的周长，均为12，唯第四类不同。0号拼板，其外框周长为10，而拼板周长为12，因为它的中部空着一格；6号拼版的拼板周长与外框周长均为10，因为它有4个格集中在一起。

表1－1　拼板的分类

将拼板归类后就可以看出这12块拼板是由5个格逐步相互变化而形成的，它们的5个格是一个整体，不能分离，犹如5个格带有磁性，虽然各个格可以转动、移动，但始终在一起，至少有一边相连。拼板中的5个格共有20条边，即20；格与格相连的边有4条，须去掉8条边，使得外形周长为12。这就说明拼板的5个格，格与格之间至少有一边相连，且最多也只有一条边相连。特例是拼板6，它有4个格集中在一起，共有5条边相连，须去掉10条边，所以其外框周长只有10。

1．2．2　拼板中格的转动变化（R变化）

1号拼板由5个格排成一长条，设为格1、格2、格3、格4和格5，且每两格能连在一起后做90°转动。如1号拼板中的格1，2、格2，3、格3，4、格4，5都可作为一个单元进行转动，如链条似的。1号拼板中的格1，2以格2为中心进行转动，若向左转则成7号拼板，若向右转即成 7号拼板。如图1－4所示（格1转向左或右，原格1取消，以格2为中心画一圆弧来表示）。转动（记为“R变化”）是相互的、可逆的。7号拼板是由1号拼板经R变化而得，也可以认为1号拼板是由7号拼板经R变化而来。

图1－4　拼板1的转动

在图1－5中举数例说明拼板中格的转动（R变化）。图形①是7号拼板中的格4，5向右转，变成2号拼板。图形②是7号拼板中的格4，5向左转而成0号拼板。图形③是L号拼板中的格1，2向左转而成 9号拼板。图形④是 9号拼板中的格4，5向下转而成3号拼板。图形⑤是 9号拼板中的格4，5向上转而成 6号拼板。图形⑥是 6号拼板中的格3，4向下转而成L号拼板。图形⑦是3号拼板中的格1，2向上转而成9号拼板。

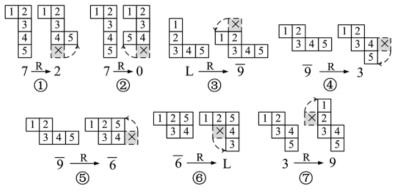
图1－5　拼板的R变化举例

1．2．3　拼板中格的移动变化（M变化）

拼板中的5个格都可移动，每次移动1格（但不能分离）。以7号拼板为例，如图1－6所示。7号拼板中格1与格2相连，将格1向下移1格后变成 5号拼板（格1与格3相连），继续将格1向下移1格便变成5号拼板（格1与格4相连），再将格1向下移1格后与格5相连，便变成7号拼板。由此可见，格1由上而下每移动1格，拼板变化一次，7号拼板通过移动（M）变化成 5，又成5，最后变成7。

图1－6　拼板7的移动

在图1－7中举出了拼板M变化的有趣例子。

图形①中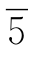号拼板中格2向左移就成9号拼板。图形②是5号拼板中格5向左移就成了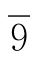号拼板。图形③是8号拼板中格1向上移变成 4号拼板；若格1继续向上移就变成2号拼板。图形④是8号拼板中格5向上移变成4号拼板；若4号拼板中格2向右移就成3号拼板。图形⑤还是8号拼板中格5向上移变成4号拼板；但这次在4号拼板中变成格1向上移则成10号拼板；格1继续向上移变成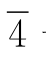号拼板；若此时将格5向上移就又变成8号拼板；经过几次M变化，最末的8号拼板却是初始8号拼板的倒图。

图1－7　拼板的M变化举例

其实这仅仅是移动（M）变化的一部分。移动（M）变化与转动（R）变化一样也是相互的、可逆的，可无限移动。

1．2．4　转动（R）变化与移动（M）变化的组合

拼板格的转动（R）变化与移动（M）变化相组合后更是变化无穷。原则上讲，12块拼板都可以相互变化。某一块拼板可以由其他拼板变化而来，而它也可以变化成其他拼板。在图1－8中，格号按序排列的1号拼板，在转动与移动的组合变化中可以变成其他十几种拼板，最后又变回到1号拼板，但它们的格的排列经过变化后就不同了。

拼板中格的变化详细过程请参阅图1－9“拼板中格的变化流程图”。

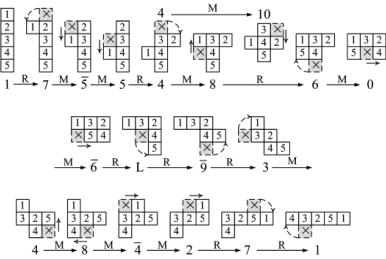
图1－8　拼板的R变化与M变化的组合

图1－9　拼板中格的变化流程图

图1－9　拼板中格的变化流程图

1．2．5　拼板的“相邻”与“互余”

从上面可以看出有些拼板的形状相互仅差一格，有的左右差一格，有的上下差一格，有的是一格旋转90°。

两拼板之间仅是上下或左右差一格的，称它们为“相邻”，如0和6，2和4，3和4等等；5和，6和也是相邻的。某拼板与某“相邻”的拼板互为“邻块”，如2和4相邻，4是2的邻块，2也是4的邻块。

若两拼板是由一端的一格旋转90°而成的，称它们为“互余”，如0和7，1和7，3和9等等。某拼板与它“互余”的拼板互称为其“余块”，如0和7互余，7是0的余块，0也是7的余块。

拼板的邻、余块数目说明了它与其他拼板的联系及活动能力。从表1－2中可以看出，拼板4和6的邻、余块最多，而拼板1和10最少。这就决定了拼板中4和6最活跃，而1和10最呆滞。所以在拼图时尽量先安排拼板1和10，最后处理拼板4和6。

表1－2　拼板的邻块和余块

拼板的“相邻”和“互余”关系在拼板可变换组合图形中起着重要的作用。许多“相邻”、“互余”的拼板能组成各种可变换的组合图形。所以熟悉和掌握拼板的“邻块”、“余块”关系，在探索“伤脑筋十二块”奥秘中至关重要。

1．3　拼板的组合图形

由若干块拼板构成的图形称为“组合图形”。组合图形形状各不相同，数量千千万万。但在某一组合图形中的拼板可以进行变换（相对位置的改变），换言之，这个图形有数种拼法而外形没有改变。这种图形称为“可变换的组合图形”。以后讲的组合图形都是指可变换的组合图形。

下面举几个简单例子来说明可变换的组合图形。

拼板2和4可以拼成的图形有数十种，但只有如图1－10所示的两种是可变换的组合图形，因为它们都是轴对称图形，把它们翻过来的图与原图是吻合的，但相对的排列改变了。图1－10①中拼板改变成4，2；而图1－10②中拼板2，变成了，4，正反面都改了。

图1－10　可变换的组合图形例1

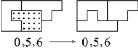
图1－11　可变换的组合图形例2

例2是拼板0，5和 6拼成的组合图形（见图1－11）。右边的图形中3个拼板的相对位置改变了，同时拼板6翻转了，但其外形没有变。

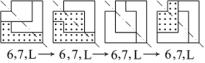
图1－12　可变换的组合图形例3

图1－12的例3中显示了由拼板6，7和L拼成的组合图形。其中拼板6和L构成的轴对称图形有两种变换：6和L组合及 6和L组合；若把6和L看做一个整体，与7号拼板拼在一起，7号拼板旋转变成 7，与拼板6和L的轴对称图形又有两种组合，故此组合图形有4种拼法，构成4幅图形。虽然外形没有改变，但其内部的排列却不相同了。

从以上3个例子可以看出，可变换的组合图形，不但变换数量有许多，而且变换方式也不一样，例1中的图形为轴对称图形；例2为拼板的相对位置的改变；例3则是两种变换复合在一起。所以变换方式多种多样，且错综复杂。

1．4　拼板组合图形变换的方式

拼板组合图形中，拼板变换的方式可分为两大类：对称型变换和非对称型变换。

在对称型变换中，根据对称形式还可细分为：①中心对称型变换（DD型）；②纵轴对称型变换（ZD型）；③斜轴对称型变换（XD型）和④矩型对称型变换（JD型）。

非对称型变换可分为：①移位型变换（E型）；②替代型变换（T型）；③置换型变换（Z型）和④隐性变换（YT型）。

记录时用英文大写字母表示对称型变换，如“DD”，“JD”，“E”，“Z”等，下标为组合图形的序号，后面也可加一括号记录参与拼板的编号。如图1－13①中的变换为纵轴对称，参与的拼板有3和4，查《组合图形汇总表》（第三篇）可知应记为“ZD4（3，4）”。对于一些特殊的变换，如替代型变换、置换型变换、隐性变换的参与拼板编号的记录方式请见各相关的章节。

1．4．1　对称型变换

符合对称型变换的图形有很多类，如纵轴对称图形、中心对称图形，矩形图形是上述两种对称图形的综合，还有斜轴对称图形。实施对称变换时，参与的拼板编号没有变化。

1．纵轴对称组合图形（ZD型）的变换

两块或数块拼板构成的组合图形如果是纵轴对称图形，那么绕纵轴将图形翻过来仍旧可放回原处，也就是该组合图形的反面图和正面图的外形是一样的，只是排列改变了。

如图1－13所示，图形①中拼板3和4构成了纵轴对称组合图形ZD4，把它翻过来后，外形是一样的，但排列由3和4变成了 和3。图形②中，拼板1，6，7构成的图形也是纵轴对称图形ZD17－1，翻转后外形没变，拼板的排列由1，7变成6，7，1。

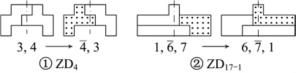
图1－13　纵轴对称的组合图形

图1－14　偶拼板组成的纵轴对称图形

纵轴对称图形的组成方式很方便。

第一种是由偶拼板组成。偶拼板0，1，8和10本身就是轴对称图形，若相互在同一对称轴上就构成纵轴对称图形。如图1－14所示，拼板0和1、0和8、0和10、1和8等等。它们的组合翻过来后与原图形一样，且排列相同，在图案中的变换并不能产生新的图案，因此在可变换组合图形中不予考虑。

第二种是互为“邻块”的相邻的两拼板构成的纵轴对称组合图形。在图1－15中，拼板2和4（两个图形）、3和4（两个图形）、4和8、4和10、5和7、5和9（两个图形）等，它们相互之间都只相差一格，所以可以拼在一起组成纵轴对称型图形，它们是可变换组合图形的重要组成部分。

大量的可变换纵轴对称图形是由两个以上的拼板组成的。在第2．3节介绍的J＇s黄金组合图形（见图1－16①，ZD53－1）是非常特殊的纵轴对称图形，不但外形漂亮，在其图形中包含有5种变换图形（见图2－14）；图1－16中的图形②是由拼板3，4，9构成的灯笼形纵轴对称图形（ZD19），图形③是由拼板0，3，10和L构成的房屋形纵轴对称图形（ZD30－1）。这能激起对组合图形的想象力，提高趣味性。

图1－15　相邻拼板组成的纵轴对称图形

图1－16　其他纵轴对称型组合图形

2．中心对称组合图形（DD型）的变换

组合图形如果是中心对称的，那么该图能以对称中心为轴心在平面内旋转180°，得到的图形仍可放回原处，但排列次序改变了。

图1－17　中心对称的组合图形

图1－17中画出了两个中心对称组合图形。图1－17①是由拼板3，7，9构成的组合图形DD3－3，经过旋转180°后外形不变，排列从3，变成了，3。图1－17②是由拼板5，2，3和6构成的中心对称组合图形DD7－2，平面内旋转180°后外形没变，排列由，3变成，3。

中心对称变换与轴对称变换的不同点在于它是在平面内旋转180°，拼板不翻过来；而轴对称变换是把图形（拼板）翻过来。它们的共同点是产生另外一个对称的图形。

3．矩形组合图形（JD型）的变换

矩形的特点是既是纵轴对称又是中心对称，所以可以翻过来，又可以旋转180°。它可变换出正、反、倒、顺四个图形。

图1－18例举了两个矩形组合图形。图1－18①是由拼板7，9，L构成的5×3矩形组合图形JD1－6。图形（b）是图形（a）的侧反面图，图形（c）是图形（a）经过平面旋转180°后得到的，图形（d）是图形（c）的侧反面图。同样，图1－18②是由拼板8，5，7和4组成的5×4矩形组合图形JD2－4，图形（a）到图形（d）是它的4种不同排列的图形。

图1－18　矩形的组合图形

4．斜轴对称组合图形（XD型）的变换

两块或数块拼板构成的图形，如以它的对角线为对称轴对称，则可以以对角线为轴，原处立体旋转180°（翻过来）后的图形与原图形重合，则该图形为斜轴对称型组合图形。

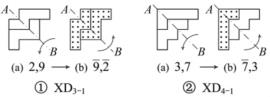
图1－19　斜轴对称组合图形及其变换

图1－19画出了最简单的斜轴对称型组合图形及其变换。如图1－19①所示，由拼板2和9构成的组合图形（a）是关于对角线AB对称，它可以AB为轴进行翻转（翻过来）成图形（b），外形没有变，但其排列改变了：由正面变成反面，即拼板的排列由2，9变成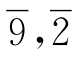（XD3－1）。又如图1－19②所示，由拼板3和 7构成的组合图形（a）经过翻转后得到了图形（b）（XD4－1），其排列也改变了。

要实施斜轴对称型变换，斜轴对称型图形的构成是关键。下面介绍几种斜轴对称型图形的构成方法。

两个互余的拼板可构成斜轴对称型图形。如图1－20中所举的4例。拼板0和7（XD1）、1和7（XD2）、3和9（XD5）、4和6（XD8）都是互余的拼板，它们构成的组合图形可以翻转，翻转后拼板的排列改变了，拼板的正反面也改变了。

图1－20　互余拼板构成斜轴对称型图形

两块偶拼板也可以构成斜轴对称型图形。如偶拼板3和10、3和L、10和L等虽然也组成了斜轴对称型图形，但它们旋转前后完全一致，如图1－21所示，不仅图形一样，排列也没有变，所以在可变换组合图形中也不予考虑。

图1－21　偶拼板构成斜轴对称型图形

由3块或3块以上的拼板构成的斜轴对称型组合图形通常是以正方形为基础、以对角线为对称轴，其外形变化多端，排列形式繁多。图1－22中举出了6种常见的外形和排列。图形①由3块拼板1，2，7构成（XD14）；图形②也是由3块拼板构成，它们为拼板3，5，8（XD15－4）；图形③由4块拼板1，2，6和7构成（XD22－6）；图形④由5块拼板组成（XD29－1）；图形⑤由6块拼板组成（XD34－9）；图形⑥由7块拼板组成（XD36－8），其中由7块拼板构成的斜轴对称型图形正好是正方形缺一格，即6×6－1＝35格，这种外形是图案中常见的一种组合图形。

图1－22　以正方形为基础的斜轴对称型图形

1．4．2　非对称型变换

1．移位型组合图形（E型）的变换

由两块或两块以上拼板构成的组合图形，经过图形内部拼板相对位置的移动（排列改变）而其外形不变的变换称为移位型变换，记录方式为E15（2，7，L）。

见图1－23中所举的例子。图1－23①中图形是由拼板6和7构成的组合图形（E2），经内部拼板移位后外形仍然不变。同样，图1－23②中图形是由拼板4和9组成（E1），图1－23③中的图形由拼板2，7，L组成（E15），图1－23④中的图形由拼板0，4，5组成（E4），经过拼板移位，均产生了外形相同但内部拼板排列不同的图形。

图1－23　移位型变换

图1－24　二次移位变换

一般组合图形中只有一次移位，产生一个新排列的图形。但也有可做二次移位、产生两个新排列的图形。如图1－24所示，图中①为由3块拼板0，4，6构成的组合图形（E5），图②为由4块拼板2，4，5和L构成的组合图形（E49）。它们经过二次移位分别产生了两个不同排列的图形。可见每移位一次就产生一个新图形。

2．替代型组合图形（T型）的变换

由两块或数块拼板构成的图形A与另两块或数块拼板构成的图形B，若A，B两图形的外形相同且能重合，那么图形A与图形B可互相替代。这种变换称作“替代型变换”。由于涉及的拼板在变换前后的组合不一样，记录时除表明类别及编号外，最好标出两组（或多组）可互相替代的拼板编号。

图1－25中显示了可以实施替代变换的若干组图形。图1－25①中有两幅图形A和B，图形A由拼板0和4构成，图形B由拼板6和7构成，它们具有相同的外形，所以它们可以相互替代，记作T4－2（0，4～6，7）。同样，图1－25②中的图形A与图形B也可以替代，即拼板0和10也与拼板6和L在构成A，B图形时可以替代（T18－3）。图1－25③中的图形A与图形B分别由3块拼板构成，这两组组合图形的外形相同也可以替代（T75－3）。图1－25④中有由拼板2和3、6和8、7和9构成的3幅相同的图形，可以相互替代，记作T34（2，3～6，8～7，9）。同样图1－25⑤中也有由拼板1和7、5和8、9和L构成的3幅相同图形（T27），可以相互替代。

图1－25　替代变换的图形

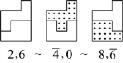
图1－26　相邻拼板组成的可替代的图形

替代型变换实施方法有：

（1）两个相邻的拼板与另两个相邻的拼板组成的两组图形可相互替代。如a，b为两个相邻拼板，c，d为另两个相邻拼板，那么a，c组成的图形可与b，d组成的图形相互替代。

从图1－26中可以看出，拼板6，0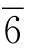是相邻的3个拼板，拼板2，8也是相邻的3个拼板，它们的组合图形2和6、0和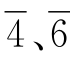和8的外形相同，可以相互替代。这种类型的图形很多，最基本的列在表1－3中。

表1－3　相邻拼板构成的可替代图形

（续表）

（2）两互余的拼板，与另两个互余的拼板构成的两个图形可相互替代。

这种类型的图形很多，常见的如图1－27所示。图1－27①中拼板0和7是互余的，拼板6和9也是互余的，那么拼板0和6构成的图形与拼板7和9构成的图形可相互替代（T9－2）。图1－27②中拼板1和7是互余的，拼板4和6也是互余的，拼板1和4构成的图形与拼板6和7构成的图形可相互替代（T19）。从图1－27③到图1－27⑦所示的5组图形都是由两对互余拼板构成的可替代的图形。

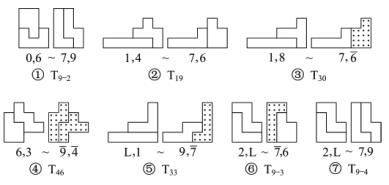
图1－27　互余滑块组成的可替代的图形

表1－4列出了由互余拼板构成的可替代图形。在表1－3和表1－4中，右下角标出了在拼图过程中使用过的替代型变换编号。可见在拼图中替代型组合图形的变换用得比较多。

3．置换型组合图形（Z型）的变换

“置换”是借用了化学中的名词。在化学的置换反应方程式中

即在反应过程中C从AB中把B置换出来了。

在组合图形的变换中，拼板A和B构成的图形，在其外形不变的前提下，拼板C从AB图形中把B置换出来。这种变换同样是可逆的，相互的。

图1－28　置换型变换（一）

图1－28中举了两个例子。在图1－28①中，拼板2和6与拼板4和6构成的图形的外形相同，所以2号拼板与4号拼板可以相互置换，即4号拼板从拼板2和6构成的图形中把2号拼板置换出来，反之，2号拼板也可以从拼板6和4构成的图形中把4号拼板置换出来。在图1－28②中，3号拼板把6号拼板从拼板4和6构成的图形中置换出来；反之，6号拼板也可以从拼板3和4构成的图形中把3号拼板置换出来。

未被置换的拼板称作“根”，被置换的拼板称作“花”，形象地表示一根上的两朵花可以互换。图1－28①中6号拼板是根，拼板2，4是花，记为Z16（62－4）；图1－28②中4号拼板是根，拼板3，6是花，则可记为Z5（43－6）。

置换型变换的实施方法有：

（1）利用能自身翻转成相邻拼板（差一格）的拼板作根，与其他两相邻拼板实施置换变换。拼板中，为自身翻转成相邻拼板的拼板，在置换型变换中常以它们作根。

以图1－28①中的置换变换Z16（62－4）为例。根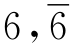是能自身翻转成相邻的拼板，拼板2，4是相邻的拼板，以作根可分别与拼板2，4构成相同的图形，即生成能互相置换的图形，所以拼板2，4可以相互置换。

表1－5给出了能实施置换型变换的拼板和它们的组合图形。表中横向为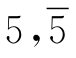及，纵向为另外的相邻拼板，交错格为它们构成的能置换的图形。

表1－5　能实施置换型变换的拼板及组合图形

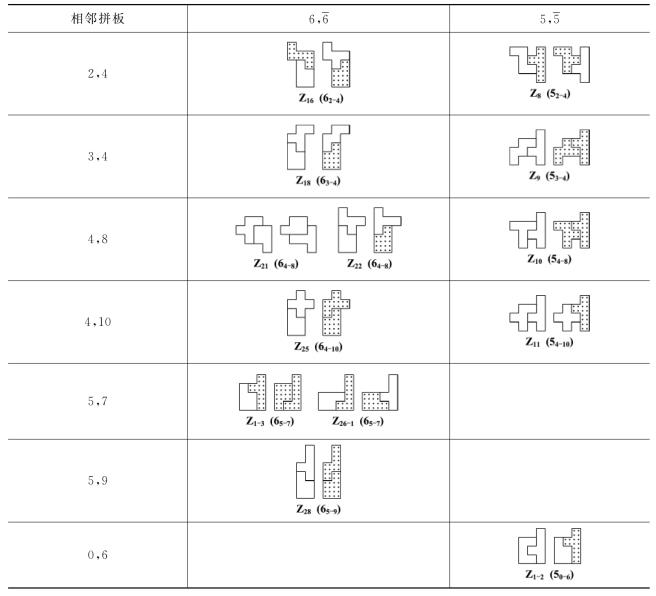
（2）6号拼板与其他互余拼板可以实施置换型变换。

由于6号拼板的特殊性质——把拼板6翻身成?，既是移位一格（相邻），又是将头部转一格（互余）。所以6号拼板还可以与其他互余的拼板构成同样外形的图形，使得那对互余的拼板相互置换。具体见表1－6所示。表中横向为互余的拼板。

表1－6　6号拼板与互余拼板实施置换型变换

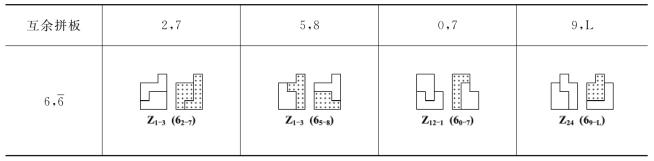
除此之外，尚有许多。图1－29中画出的几例都是可以置换的图形。置换在拼图中极其重要，尤其是用于解决第十二块拼板的难题。后面将详述。

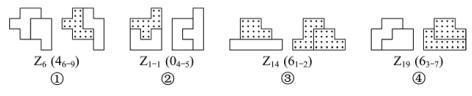
图1－29　置换型变换（二）

4．隐性型组合图形（YT型）的变换

组合图形中拼板变换的方式虽然各不相同，但都在相同外形的前提下实施，或在图形内部变换（D型和E型），或相互变换（T型和Z型）。这种在外形上显而易见，较容易认识的，称之为“显性变换”。相对而言，在组合图形不同外形的情况下进行变换则较难识别，较隐蔽，故称之为“隐性变换”。

为了说明隐性变换的特点，下面举出两例。

例1如表1－7所示，拼板4，5与拼板8，9都可构成外形相同的图形α1，α2和β1，β2。

在显性变换中，拼板4，5与拼板8，9可实施两组替代型变换：第一组为替代型变换T54，替代的为图形α；第二组为替代型变换T51替代的为图形β。显然，图形α和图形β是不同的。

表1－7　隐性变换（一）

在隐性变换中，图形α虽然与图形β是不同的两种图形，然而，拼板4和5原构成的图形为α1，可以变换成图形β1（见表1－7），从而取代由拼板8和9构成的图形β2，替换出拼板8和9，即α1→β1；替换出来的拼板8和9构成图形α2填入原图形α1的位置，即β2→α2；这样就完成了一次隐性变换（YT8）。本例的隐性变换是通过两对替代型变换的组合完成的。

例2如表1－8所示，拼板1，2，5和6均可分别构成图形α和β。其中，拼板1和5构成图形α1，拼板2和5构成图形α2，这实际上是置换型变换Z7（51－2）；拼板2和6构成图形β1，拼板1和6构成图形β2，这是置换型变换Z14（61－2）。由表1－8中可看出，图形α1＋β1是由拼板1，2，5和6组成，图形α2＋β2也是由拼板1，2，5和6组成，那么图形α1＋β1可与图形α2＋β2互相替代（YT2）。此例是利用两个置换型变换组合后实施的隐性变换，比例1更隐蔽、更复杂。

表1－8　隐性变换（二）

隐性变换是组合图形变换中最深奥的变换，但它有助于图案最后两块拼板的拼图，值得我们对它进行探索研究。

1．4．3　组合图形变换方式小结

（1）组合图形的变换要有奇拼板参与，大多数变换都离不开奇拼板的正面、反面的变换。因为变换的产生除了排列变化外，主要通过拼板正反面的变化。

（2）偶拼板虽然正反面是同一形状，但在某些变换中，为了能直观和保持图形的完整性，有时也保留偶拼板的位置。如图1－30中的6×6－1形式的旋转型变换（XD36－22）。在图1－31①中保留了偶拼板3和10，较容易看出图1－30①中图形（b）是图形（a）旋转后的图形，这是一个旋转型图形。而在图1－30②中把拼板3和10删去，就较难看出图形（b）是图形（a）旋转后的图形。其实在旋转中拼板3和10也是反过来的，一起参加变换，只是它们的反面和正面一样，被忽略而已。

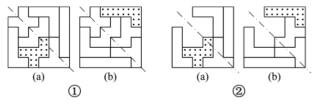
图1－30　6×6－1的斜轴对称型变换

（3）表1－9汇总了本节所介绍的6种变换方式。表中A，B，C，D表示拼板，α，β代表图形。

表1－9　拼板变换方式汇总表

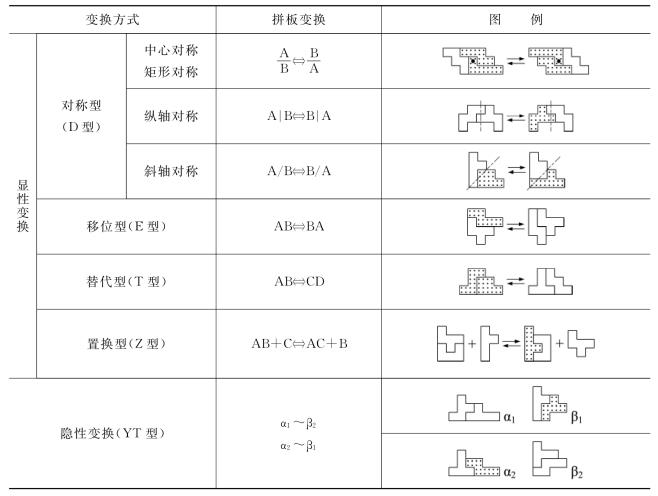
（4）用12块拼板可以拼出许许多多可变换组合图形，我们仅对在本书拼图中出现的可变换组合图形进行了整理，汇编在第三篇《表集》中的“组合图形汇总表”内。总计有DD型变换24组（42幅），JD型变换7组（69幅），XD型变换36组（107幅），ZD型变换63组（98幅），E型变换148组（155幅），T型变换78组（104幅），YT型变换9组（9幅），Z型变换34组（39幅）。相信随着拼出图案的增加，可变换组合图形会变得越来越丰富。

1．5　组合图形中拼板间的关联

1．5．1　链式关联

若有3块拼板A，B和C组成的图形中，拼板A，B可变换成BA从而排列成BAC，而正好AC又可变换成CA，使排列变成BCA。这种关联中只有先完成AB成BA的变换才能产生AC成CA的变换，A，B，C像链的三个环。该变换是可逆的，倒过来变换也一样，可往返变换。整个变换是：ABC～BAC～BCA～BAC～ABC…像钟摆一样可来回变换，所以链式关联也可称为“摆式关联”。组合图形ABC通过两次变换生成3幅组合图形。链式关联参与的拼板可以有4块、5块……变换可以有三次、四次……每增加一次变换就增加一幅图形（一种新排列的图形），因此形成一个族，这个族的图形数量等于变换次数加1。

图1－31所示为三块拼板3，4，9的链式关联。图形①的排列为4－3－9，其中4－3组合是纵轴对称图形，通过变换ZD4可变成3－4组合，即图形②，排列为3－4－9；此时的4－9组合又可以通过移位型变换E1变成图形③，排列为3－9－4。从图形①到图形③是通过两次变换生成了3幅图形。必须注意，原来4和9之间并没有变换关系，是通过3和4的变换后才有4和9的变换。假设从图形①到图形③的变换为顺向，那么从图形③到图形①的变换则为逆向。变换可在此范围内往返进行。

图1－31　链式关联（一）

图1－32　链式关联（二）

图1－32中举出了另一例链式关联。图形由拼板0，1，7构成。图形①的排列为1－0－7，若将0－7组合做斜轴旋转变换XD1，可获得图形②；若将图形②中1－7组合做斜轴旋转变换XD2则变成图形③的排列7－1－0。图形也是经过两次链式关联的变换，产生了3幅图形。

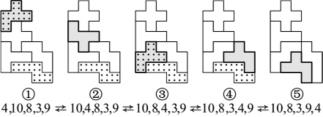
图1－33　链式关联（三）

图1－33所示是五块拼板4，10，8，3和9的链式关联。图形①的排列为4－10－8－3 －9，其中组合4－10为轴对称图形，经ZD8变换后成图形②；在图形②中组合4－8也可进行纵轴对称变换ZD7，成为图形③；图形③中的拼板3－4组合为纵轴对称型ZD4，变换后成图形④；图形④中拼板4－9组合又可做移位变换E1，变换后成图形⑤。此例的链式关联有4次变换，环环相扣，产生5幅图形。变换可以由图形①到图形⑤，也可以从图形⑤到图形①。值得注意的是，在变换中，4号拼板从上方逐步下降到下方，也可以从下方逐步升到上方，显得很活跃。

1．5．2　复式关联

一个组合图形中有几个变换，而且变换时各不相干，这种关系的变换称之为复式关联。

图1－34　复式关联

图1－34是由拼板1，5，6构成的图形。整个图形可以做斜轴旋转XD15－2，其中由5和6拼成的图形也可单独进行旋转XD4－2，由此两个旋转变换是各不相干的。当拼板1，5，6整体旋转时不用考虑拼板5和6的旋转；组合5－6旋转时也不会影响1，5，6的整体旋转。总之，在复式关联中两个变换各不相干，都可单独进行变换。所以，最终产生的图形数等于2×2＝4幅。

图1－35画出了由拼板0，4，6，9，10和L组成的5×6矩形图形JD4－1的复式关联。矩形本身就有4个变换的图形（图中的图形①到图形④），而其中拼板4和9又可作移位变换E1，产生两种变换图形，一共产生2×4＝8幅图形，图1－35中的8幅图形都是它的变换图形。所以该矩形图形的变换具有各不相干的两种类型（矩形变换与移位变换各不相干），属于复式关联。

图1－35　5×6矩形图形JD4－1的复式关联

1．5．3　混合式关联

若一个组合图形中，拼板既有链式关联，又有复式关联，则称该图形具有混合式关联。

图1－36　混合式关联

图1－36所示为由拼板0，2，3，6，9，10和L组成的组合图形，整个图形是（6×6－1）的斜轴旋转图形XD36－11。现在分析一下该组合图形的变换。

首先，该图形可以斜轴旋转，图形④、⑤、⑥是图形①、②、③经过旋转后的图形。图中3号拼板也参与了旋转，因为它的正反面是一样的，所以旋转前后没有变化。在图中取掉3号拼板不影响旋转变换，但识别比较难些。

拼板0和10构成的图形是对称型图形，虽然它们可以变换，但0和10是偶拼板，正反面是一样的，所以变换后仍旧是原样。

拼板2，6，9和L组成的图形中，拼板可以进行移位变换E55，图形①和图形②就是它们相互移位的两个图。

在图形②中，拼板6和9又可以进行斜轴旋转XD9而得到图形③。但拼板6和9的旋转是在拼板2，6，9和L移位的前提下才能进行，所以它们是链式关联。

由此可见，图1－36的变换由两部分组成：整体图形的旋转变换；部分图形的移位与旋转。这种复式与链式的混合式关联一共可产生2×（2＋1）＝2×3＝6种图形。

【注释】

[1]我国的计数之字曰“数码”。图1－1中的数码符号参见1912年12月（民国二年）商务印书馆《新字典》（朱祖谋主编，蔡元培序）中“石”部“码”字条，第276～277页。

[2]选用L表示第十二块拼板，有两层意思。第一，除0外它位于后11位，用阿拉伯数的1和中文的“一”相组合而成英文字母大写的L，形象化了，便于记忆；第二，L在英文26个字母中正好排在第十二位。