由组合图形作基础，创造出新图案

第2章　J＇s图案编码法及图案可变换系列

2．1　J＇s图案编码法

拼板有了编号，就可以对拼板拼出的各种图案进行编码，以便收集、归纳图案，汇编成图集。

J＇s图案编码法采用图案的4个角的拼板编号。号码由左上角、右上角、左下角、右下角及紧挨右下角上面的拼板的编号组成。该编码的前4位为正位码，字号一样大，同一水平写，而末位写为正位码的下标，如图2－1所示。编码应写在图案的右上方。

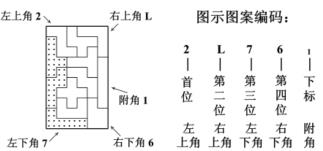
图2－1　J＇s图案编码法

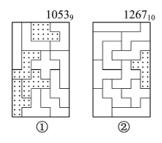
图2－2　J＇s图案编码实例（一）

图2－2中举出两个编码实例，图中图案①的编码为10539，图案②的编码为126710。因为10号拼板不可能出现在图案的四个角上，所以不会出现在图案的正位上，即不会与拼板1和0相混淆，因此图2－2①所示的图案编码决不会是10，而只能是1和0。但10号拼板可以出现在附角的编码里，如图2－2②所示的图案编码中附角为10，因附角只取一个，所以不可能产生1和0两个附角号，写10只能表示是10号拼板。

图案编码的排列按编码的自然数排列。编码为12进位制，0是第一位，L是最后一位，总的排列次序为：0，1，2，3，4，5，6，7，8，9，10和L。由末位（即附角编号）开始采用12进位制到第四位、第三位、……直至首位，如01238，01269，0127L，014710和053L6，等等。

在外框为5×12的图案中，1号拼板可能横在图案的上方（或下方），则在它的左上角以“1”表示，右上角以“－”表示，不用0或空缺，以避免产生编码上的混乱。如图2－3中的图案①，图案的编码为1－57L。同样，在外框为4×15的图案中，拼板5和7可能横在图案的上方（或下方），则取左上角为5（或7），右上角为“－”。图2－3中图案②的编码应为7－8L2。

图2－3　J＇s图案编码实例（二）

在图案编码排列次序中，“－”排在“0”之前。如图案1－57L排在1057L之前，167－0排在167010之前。

2．2　图案的相互关联及可变换系列

图案由12块拼板组成，其中有的包含各种可变换组合图形，

组合图形的关联性和变换性决定了图案的关联性和变换性，从而形成了图案的可变换系列。

2．2．1　图案的自变系列

图案是矩形图形。矩形图形如前所述可以有正、反、倒、顺4种变换，衍生为4幅图案，它们实质上是同一幅图案。

图2－4　图案的自变系列图

设一幅图案置于直角坐标系的第Ⅰ象限，那么在Ⅱ，Ⅲ，Ⅳ象限生成的另3个图就是它的反面、反倒、正倒图。每个象限的图是同一个图案的4种表现之一，因而有4个编码，如图2－4所示。这种由图案自身变异而生成的4幅图案就是图案的自变系列。

为查阅方便，我们设定这4幅图案中自然数编码最小的图案为主图。在图集中主图位于直角坐标系的第Ⅰ象限，其余各象限图为该主图的自变系列图。图2－4中主图编码为017L8，其自变系列图的编码分别为107L4，7L105和L7018。

每幅图案都有自变系列图。在拼图中，有时拼成图2－4中的017L8，有时拼成如图2－4中的7L105，其实两次拼成的是同一图案，它们是同一自变系列的两幅图案，一幅是第Ⅰ象限图，一幅是第Ⅲ象限图。

2．2．2　图案的变换系列

在图案中如包含可变换的组合图形，那么图案因其中的可变换组合图形而变换衍生成另外一幅图案。衍生的数量由其中组合图形的变换而定。

1．图案中含有一组组合图形的变换系列

如图2－5①所示。图案中的拼板2和9为斜轴对称型组合图形XD3－1，可进行旋转型变换成和 ，因而使图案衍生成两幅，组成一个系列的两幅图。由于这两幅图案除了XD3－1变换外，其他拼板均无变动，也没有涉及到4个角及附角的拼板，所以两幅图案的编码没有变，都是13L610（见第9章〈6〉－1－171系列）。

但在图2－5②中，也是拼板2和9的变换（XD3－1），而其位置在右上角，变换后使右上角拼板变了，所以图案的编码也改变了，由126710变成196710（见第9章〈6〉－2－61系列）。

有的图案中变化的拼板正好在附角的位置上。如图2－5③所示，拼板2和4是对称型变换ZD1，正好在附角位置上。图案编码由178L2变成178L4，它们也是同一变换系列的两幅图案（见第9章〈6〉－2－84系列）。

含有一组组合图形的图案，经过一次变换衍生了另一幅图案。它俩犹如一对孪生姐妹，构成一个变换系列。

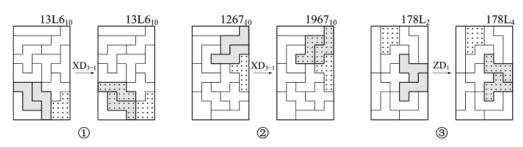
图2－5　含有一组组合图形的变换系列

2．图案中含有两组或三组组合图形的变换系列

图2－6所示为包含两组组合图形的图案，且这两组图形的变换各不相干。图形中拼板2 和4、8和L是两组对称型变换组合图形（ZD2和ZD13），变换时各不相干。从图中可以看出，图形①和②中拼板2，4进行了变换而拼板8，L未变换；图形③和④中则是拼板8，L变换后拼板2，4又进行一次变换。由此可见，有两组各不相干的变换可以形成2×2＝4种不同排列的图案。涉及图案编码的只有两个右下角，这就产生了两个编码的4幅图案的变换系列（见第9章〈6〉－2－82系列）。

图2－7给出了含有三组各不相干的可变换组合图形的变换系列。其中包括拼板3和7的旋转型变换XD4－1、拼板4和10的对称型变换ZD8和拼板2和9的旋转型变换XD3－1。图案中这三种变换各不相干，互不影响，所以就衍生成2×2×2＝23＝8种不同排列的图案，成为一个变换系列。因为变换涉及左下角拼板的变换，故该系列的8幅图案只有两个编码：67281和67981（第9章见〈6〉－3－39系列）。

图2－6　含有两组组合图形的变换系列

图2－7　含有三组组合图形的变换系列

3．图案中含有链式关联的组合图形的变换系列

图2－8给出了含有链式关联的可变换的组合图形的变换系列。图案0L641中含有拼板3，6，7链式关联的组合图形。图案①中拼板6，7可移位变换E2成图案②；在图案②中拼板3，6可作对称型变换ZD5－1成为图案③；在图案③中拼板3，7可通过旋转变换XD4－1成图案④。经过三次链式变换（6，7）→（3，6）→（3，7），生成了4幅图案，形成了一个系列（见第9章〈6〉－2－51系列）。

图2－8　含有链式关联组合图形的变换系列

4．图案中含有复式关联的组合图形的变换系列

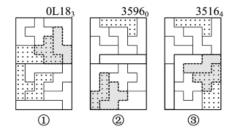
图2－9　含有复合关联组合图形的变换系列

在如图2－9所示的图案中，图案0L183由3个组合图形复合构成。上部的组合A为由6块拼板0，4，6，9，10和L组成的矩形变换图形JD4－1，下部的组合B为由拼板1，2，3，5，7和8组成的矩形变换图形JD4－2，在矩形A内由拼板4和9组成的组合C可作移位型变换E1。下面讨论一下该图案的变换系列。

组合A，B各自有4个变换图，那么就有16种不同排列的图案。但注意，当组合A取第Ⅱ象限（反面），同时组合B也取第Ⅱ象限（反面），那就是整个图案取了第Ⅱ象限（反面），与图案的自变系列中的第Ⅱ象限（反面）重复；同样在第Ⅲ、第Ⅳ象限也一样。所以有一半是重复的，实际上只有8种。由于组合C的4和9的移位变换与组合A，B的变换不相干，故可获得两倍的图案，即有16幅图案。另外，当图案变换到图案②35960时，组合A加上组合B中的1号拼板后成了（6×6－1）的旋转型变换XD36－7，旋转后得到图案③35164；同时，图案③中的组合A含有4种变换，加上拼板4 和9的变换E1就又有8种了。但这与前面的变换是链式关联，所以总的变换系列图案有16＋8＝24幅。

如图2－9所示图案的变换系列有24幅图案，具体可查阅第9章《图案变换系列一览表》中系列〈6〉－4－1。

5．图案中含有混合关联的组合图形的变换系列

如图2－10所示的图案15L62中，组合A是由拼板0，1，4，5，7，9和10组成的（6×6－1）旋转型变换XD36－6；组合B由拼板8，L组成对称型变换ZD13；组合C由拼板2，6与3，8组成替代型变换T23－2；组合D由拼板3，6组成对称型变换ZD5－1；组合E由拼板4，8组成对称型变换ZD7。

看一下该图形的变换过程。

图案①中组合B拼板8和L经ZD13变换后成图案②。

图案②中组合C的拼板2，6与拼板3，8进行T23－2替代变换后成图案③。

在图案③中组合D拼板3，6做了ZD5－1对称型变换后成图案④。

图案⑤～图案⑧是图案①中组合A作旋转变换XD36－6以及分别实施组合B，C，D的变换。

在图案⑧中出现了组合E，进行对称变换ZD7后得到图案⑨。

在图案⑨中又产生了组合D，经ZD5－1变换后得到图案⑩。

由此可见，组合A与组合B，C，D是复式关联；组合B与组合C、组合C与组合D是链式关联；组合E是独立的，与组合A是链式关联。所以该变换系列的总数为2×（2＋1＋1）＋2＝10幅图案（见第9章〈6〉－3－32系列）。

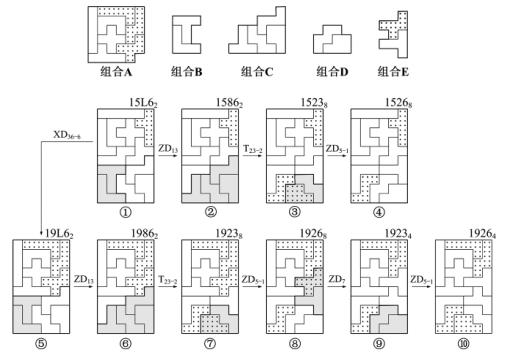
图2－10　含有混合关联组合图形的变换系列

6．图案中组合图形的隐性变换

如图2－11所示，图案57892中，拼板4，5与拼板8，9构成的图形，虽然外形不同，没有关联，其实它们是隐性变换关联YT8。在图案①中拼板4，5可以组成拼板8，9构成的图形，而拼板8，9也能组成拼板4，5构成的图形，因此它们可以互相替代，构成了图案②的图案，组成一个变换系列（见第9章〈6〉－2－116系列）。

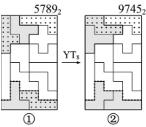
图2－11　含有隐性变换的变换系列

7．副图——变换中某拼板编号消失情况时的编码处理

在可变换系列图集中，图案编码中有的拼板编号（在4个角上的正位码）在变换中会消失。如可变系列〈6〉－1－209中，3幅图案编码应为17L69，697L10和69872。但编码17L69［见图2－12①中图案（a）］中1号拼板在变换中消失了（即经变换后得到的两幅图的编码为697L10和69872），且这3幅图案分别位于17子部与6子部（见第3章表3－8）。为了把图案归纳在一起，或尽量靠近，所以对于编码为17L69的主图，另设对应的副图6L710（即图2－12①中图案（b），其实图案6L710是图案17L69的第Ⅳ象限图），这样变换系列的3幅图均可归在6子部，比较容易了解它们的变换过程。

为了便于查阅，在表集和图集中均收集17L69和其副图6L710。在表集（第三篇）中，附有副图的主图编码下面加一道黑线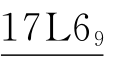：，对应的副图编码前冠以符号?，以示区别。在图集（第四篇）中，为了表明在变换过程中主、副图之间的关系，采用了如图2－12②所示的表示方法。图中，主图17L69的编码加上双实线框，表示其附有副图，并在其图案下表明副图序号（6f－232）、编码6L710、在编码前加符号?以及副图的象限（Ⅲ），见图2－12②中的（a）；在副图中，编码6L710前不仅加上符号?，还用虚线框起来，在其图案下表明相应主图的序号（6－1530）、编码17L69以及主图在该副图自变系列图中的象限（Ⅲ），见图2－12②中的图案（b），便于相互查阅。

图2－12　变换中拼板编码消失时的编码处理

2．2．3　图案变换系列小结

（1）图案中若含有各种可变换的组合图形，图案就会因组合图形的变换而衍生成变换系列图案。

（2）图案中含有各不相干的可变换组合图形时，可变换组合图形的组数与生成图案变换系列的数量关系如表2－1所示。

表2－1　可变换组合图形（互不相干）的组数与变换系列中图案数量的关系

（3）图案中含有链式可变换组合图形，那么变换系列图案数量等于变换数量加1。

若图案中既有不相干的变换组合图形，又有链式可变换组合图形，则系列图案的数量等于不相干的变换生成的数量加上链式变换数量。

（4）图案无论是否含有可变换组合图形，因其本身是矩形，就可以因变换而自成一个系列，这就是自变系列。自变系列图案数量都是4幅，可采用直角坐标系的四象限表示法，自然数编码最小的图案为主图，位于第Ⅰ象限。所以图集中收集的图案的实际数量是主图图案数的4倍。

2．3　J＇s黄金组合图形及黄金图案

J＇s黄金组合图形是个奇妙的可变换组合图形，含有黄金组合图形的图案就是黄金图案。

2．3．1　黄金组合图形

黄金组合图形的外形似古钱形，由拼板0，3，4，5，8和10组成，整体是个轴对称图形，如图2－13所示。除外形对称外，该图形中还包括5种不同的变换组合图形，如图2－14所示。在图2－14中，图形①为组合A，由拼板3，4组成的对称型变换ZD4；图形②为组合B，由拼板4，8组成对称型变换ZD7；图形③为组合C，是拼板4，10构成的对称型变换ZD8；图形④为组合D，是由拼板0，5，8和10构成的对称型变换ZD33－1；图形⑤为组合E，拼板0，3和5构成移位型变换E3。

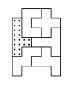
图2－13　黄金组合图形

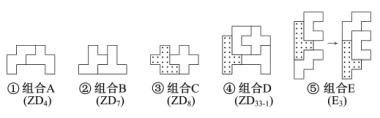
图2－14　黄金组合图形中包含的5种变换组合图形

4号拼板是这个图形中最活跃的拼板。如图2－15所示。

在图2－15中，图形①中4号拼板通过组合A的ZD4变换从左下角到了右下角，成了图形②；图形②中4号拼板又通过组合B的ZD7变换从右下角向上移成图形③；在图形③中4号拼板通过组合C的ZD8变换上升到右上角成图形④；在图形④中，组合E中拼板0，3和5经过E3移位变换成图形⑤；到了图形⑤，4号拼板又通过组合A的ZD4变换成图形⑥，此时4号拼板已位于左上角；在图形⑥中，组合D拼板0，5，8和10通过ZD33－1变换成图形⑦；图形⑦中的4号拼板通过组合C的ZD8变换位置下降，成图形⑧；图形⑧中组合E经过E3移位变换成图形⑨；图形⑨中4号拼板通过组合B的ZD7变换又回到了左下角成图形⑩；图形⑩中再次出现组合D，经ZD33－1变换成的图形与图形①完全一样。

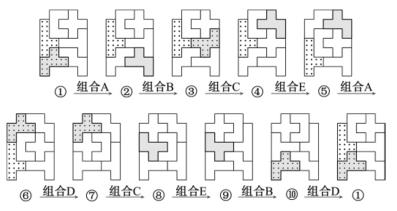
图2－15　活跃的拼板4

组合图形经过10次变换，最终与原来起点一样，4号拼板在变换中逆时针移动了一圈。这是一个奇妙的可变换组合图形，它综合了链式关联与复合关联，4号拼板可以作循环变换而顺时针或逆时针移动，无穷无尽。变换是可逆的，4号拼板可以以任何一个位置作为起点，永无止境。

2．3．2　J＇s黄金图案——包含黄金组合图形的图案

图2－16是J＇s黄金组合图案。图案①6L571中包含有黄金组合图形的因素。图案①中拼板5和9是对称型变换ZD11，变换后成图案②6L971。在图案②中又含有拼板4和9的移位变换E1，变换成图案③6L971，在此图案中便出现了2．3．1节中所述的奇妙古钱形组合图形。

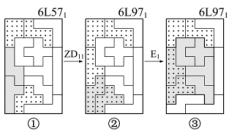
图2－16　J＇s黄金图案

由于组合图形中的4号拼板三次移到图形的左下角而与图案中的9号拼板组成4和9的移位变换E1；当4，9变换时，图案内拼板0，3，5与拼板0，5，8，10等进行着与它不相干的变换（当4和9变换时，0，3，5也可变换，或0，5，8，10也可变换）。所以整个变换系列的图案数为1＋3＋2×（2×4）＝20幅。

关于J＇s黄金图案的变换系列详见图集，可查第9章〈6〉－4－12系列。

2．4　图案的“全正图”、“全负图”及正负指数

2．4．1　“全正图”与“全负图”概念

图案中的拼板有正面放的，也有反面放的。若图案中的拼板全部是正面放的，称为“全正图”，若全部是反面放的称为“全负图”。拼板中的偶拼板（拼板0，1，3，8，10和L）的正反面是相同的，所以在“全正图”、“全负图”中偶拼板是同样的，即偶拼板可以构成“全正图”，也可以构成“全负图”。关键是奇拼板（拼板2，4，5，6，7和9），它们的正面和反面是不同的，“全正图”中要求奇拼板都是正面放的，“全负图”中要求奇拼板都是反面放的。

如图2－17所示。图2－17①中图案（a）是“全正图”07153，图中奇拼板2，4，5，6，7和9都是正面放的，偶拼板自然是正面的；它的反面图70512（见图2－17①中图案（b））是“全负图”，当然奇拼板都是反面放的。图2－17②也是如此，图案06793是“全负图”，它的反面图图案（b）是“全正图”。

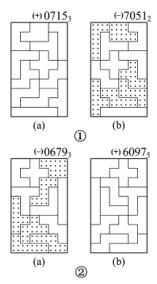
图2－17　“全正图”与“全负图”

“全正图”与“全负图”实质上是一幅图案的两个象限图。在图案编码的排列中以自然数次序排列，所以有“全正图”、“全负图”之别。“全正图”在图案编码前加（＋），如（＋）07153等；“全负图”在图案编码前加（－），如（－）70512等。

2．4．2　“全正图”与“全负图”的变换特性

（1）在可变换系列图案中，变换拼板不涉及奇拼板，仅在偶拼板中进行，那么图案虽然经过变换，其“全正图”与“全负图”的性质不变。

如图2－18所示。图案（－）05183（见图2－18中图案①）是“全负图”，图中拼板8和L组成对称型变换ZD13。但8和L是偶拼板，它们的变换（翻身）不影响全正图的性质；图形②就是8和L变换后的图案（－）051L3，仍是“全负图”（见第9章〈6〉－1－21系列）。

（2）在可变换系列图案中，虽然奇拼板参与变换，若仅为平移而没有翻转，图案的“全正图”与“全负图”性质也不会改变。

如图2－19中图案①所示，图案（＋）27651是“全正图”，其中奇拼板0，7与4，L作替代型变换T14，变换后成图案（＋）2L651（见图2－19中图案②），因是平移，所以仍是“全正图”。在图2－19图案②中，拼板2，4，L与0，5，6又构成替代型变换T68，变换后成图案③（＋）2L659，因替代也是平移，所以仍是“全正图”。（见第9章〈6〉－2－114系列）。

图2－18　仅有偶拼板参与变换时的“全正图”或“全负图”

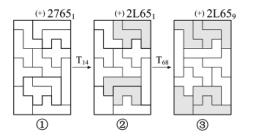
图2－19　奇拼板参与平移变换时的“全正图”或“全负图”

（3）如果图案中奇拼板在变换中有翻转的，即正、反面发生了变化，就会改变图案的“全正图”与“全负图”的性质。

如图2－20所示。图案（－）0627L（见图2－20中图案①）是“全负图”，图案中拼板1，2，7构成旋转型变换XD14，变换后成图案0621L（见图2－20中图案②），由于变换中拼板1，2，7由原来的反面变成正面（1号拼板虽然没变，其实也变成正面），而其他奇拼板没有变，所以变换后既不是“全正图”，也不是“全负图”（见第9章〈6〉－1－40系列）。

图2－20　奇拼板参与翻转变换时的“全正图”或“全负图”

图2－21　复杂变换时的“全正图”或“全负图”

（4）图案的复杂变换在图案“全正图”、“全负图”的变化中起着微妙的影响。

在图2－21中，图案①（＋）13679是“全正图”，其上部拼板3，4，8构成对称型变换ZD18－2，变换后成图案②18769，因在变换中4号拼板由正变反，而下部没有改变，仍是正的，所以图案就不可能是“全正图”了。但图案18769中下半部分拼板2，5，6，7，9，10和L构成了6×6－1旋转型变换XD36－30，变换后成图案③（－）18759，下部拼板2，5，6，7和9翻转后都成了反面，与上部的4号拼板（已是反面）一起，全部奇拼板都是反面的，所以成了“全负图”（见第9章〈6〉－3－29系列）。

在图案中奇拼板常常是正面和反面同时存在，所以绝大多数图案都不是“全正图”或“全负图”。为了便于观察奇拼板的正、反面在拼图中的变化，将奇拼板的反面涂另一种颜色（本书采用小圆点表示奇拼板的反面），这样图案中奇拼板的正反面情况就一目了然。图案中奇拼板的正、反面的个数和正、反面的变化是层出不穷的，全正、全负仅仅是其中一个特例。

2．4．3　《图案“全正图”、“全负图”索引》

图案的“全正图”和“全负图”在其图案编码前分别加（＋）和（－）。如（＋）013L6为“全正图”，（－）05183为“全负图”。

在图集中要查阅“全正图”和“全负图”，可先查阅下面所述的《图案“全正图”索引》和《图案“全负图”索引》，根据索引就可查阅到。

1．《图案“全正图”索引》

如表2－2～表2－4所示。

表2－2　〈6〉分部全正主图编码一览表

表2－3　〈5〉分部全正主图编码一览表

表2－4　〈4〉分部全正主图编码一览表

2．《图案“全负图”索引》

如表2－5～表2－7所示。

表2－5　〈6〉分部全负主图编码一览表

表2－6　〈5〉分部全负主图编码一览表

表2－7　〈4〉分部全负主图编码一览表

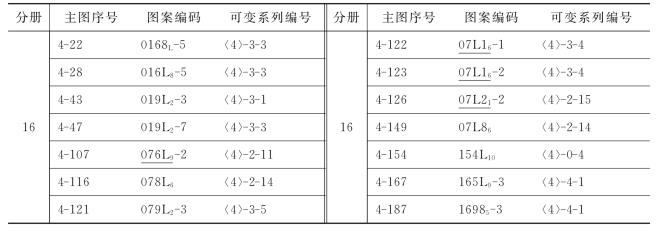
2．4．4　正负指数K

1．正负指数K的定义

为了描述图案中各个奇拼板的正反情况和正反个数，设置奇拼板的正负指数K。正负指数规则为：①奇拼板正面放置时记为（＋），反面放置时记为（－）；②采用二进位计数方法，设（＋）为0，（－）为1；③6块奇拼板按2，4，5，6，7，9程序排列，2为最高位。按二进制，2的权重为32，9的权重为1；④6块奇拼板的正反排列共有26＝64种不同的方式。根据上述规则可得出正负指数K的数值范围为0～63，其中K＝0对应全正图，K＝63对应全负图。表2－8中列出了奇拼板不同排列时对应的正负指数K的数值。

表2－8　正负指数K值表

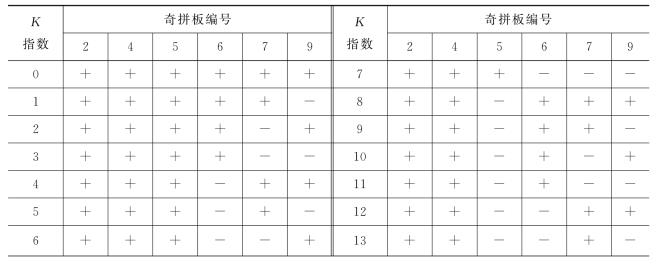
（续表）

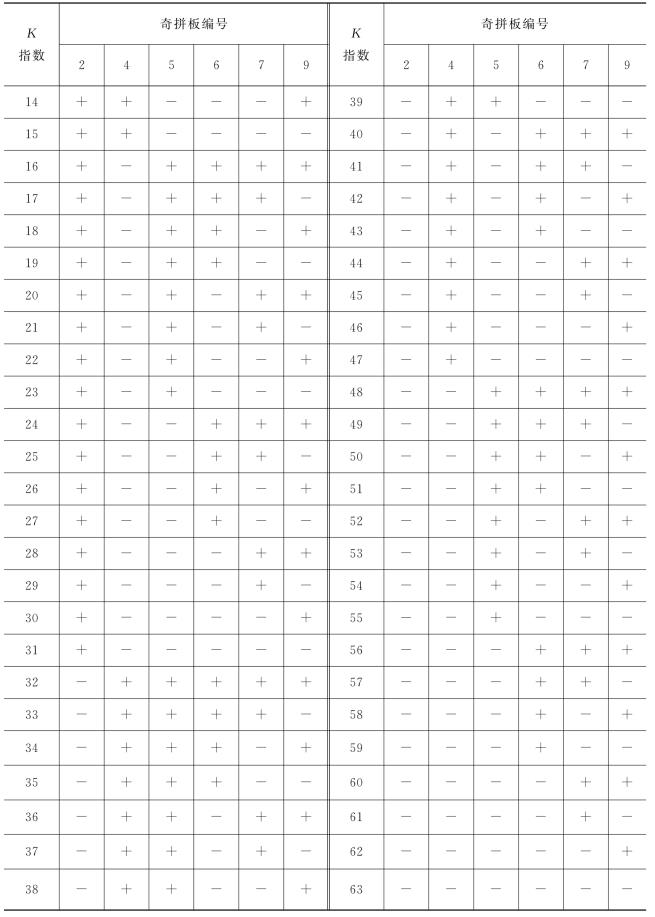
2．正负指数K在图案变换中的作用

图案可变换系列的变换主要（绝大部分）是奇拼板的变换，所以奇拼板的正负指数K也就是图案的正负指数。我们可以通过K的变化来了解图案的变化过程。

如表2－9所示，表中列出了12个〈6〉分部的图案编码及其正负指数K。

表2－9　图案编码及其K指数

下面试分析K的作用。

首先，全正图的正负指数K＝0，全负图的正负指数K＝63。例如，图案08L69－3为全正图，它的正负指数K＝0；图案806L5是图案08L69的反面图，全负图，它的正负指数K＝63。

其次，图案的正面图与反面图的正负指数K之和为63。序号3图案0L981－5中拼板2，5，7是反面放的，拼板4，6，9是正面放的，K＝42；序号4图案L0896是图案0L981的反面图，拼板2，5，7是正面放的，拼板4，6，9是反面放的，K＝21，两者之和为63。这样的例子很多。如表中序号5与序号6、序号7与序号8的图案均互为正反面，它们的正负指数K之和也均为63。

第三，有了图案的正负指数K，就可以了解图案中奇拼板的正、反面配置与分布。如K＝7，就是拼板6、7、9反面放，拼板2、4、5正面放；K＝27，则4、5、7、9反面放，2、6正面放；K＝21，是4、6、9反面放，2、5、7正面放，等等。

这种例子很多。变换越复杂，用K来描述就越容易理顺变换的来龙去脉。如前所述的黄金图案中4号拼板的不断变换也可用K来描述。在黄金组合图形中只有4号拼板和5号拼板是奇拼板。当4号拼板在黄金组合图形中循环变换一周时，奇拼板4和5有4种排法，对应的正负指数分别为0，8，16和24（见图2－20）。包含黄金组合图形的黄金图案6L971（见图2－21中图形③）中，拼板2和6是反面放的，拼板7和9是正面放的，因此黄金图案6L971的K值在36，44，52和60这4个数字中变化。当黄金图案6L971中4号拼板有两次移到黄金组合图形左下角，并与9号拼板组成4和9以及5和9的移位型变换，增加了3幅变换图案，K值也增加了两个：53和61。

在第四篇的图集中，正负指数K值用圆圈圈起来，标在图案的左上角。其自变系列中的另外三个象限中图案的K值读者可根据规则自行判定。

2．5　可变换组合图形在拼图中的应用

在图案的拼搭中，运用各种拼板演变和可变换性质及各种可变换组合图形，能加速拼图并组成图案的可变换系列，创造出更多图案。

2．5．1　由原单一图案衍生成一个可变换系列图案

在第10章《组合图形一览表》中收录了各种类型的组合图形，可用来对照所拼成的图案。如图案中含有可变换组合图形，那么该图案就可衍生成一个系列，从而增加图案的数量。

图2－22　可变换组合图形应用例1

例1　如图2－22所示，图案①0L135中有拼板2和4的对称型变换ZD2，能衍生出图案②，从而形成一个系列、两幅图案。图案的编码没有受变换的影响，都是0L135，但K值却变了（见第9章〈6〉－1－108系列）。

例2　如图2－23所示。图案①08671中有两个互不相干的变换组合图形，它们是拼板2，4的对称型变换ZD1和拼板3，7的旋转型变换XD4－1。于是图案就衍生成一个变换系列，从图案①到图案④生成2×2＝4幅图案（见第9章〈6〉－2－32系列）。

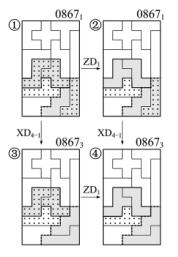
图2－23　可变换组合图形应用例2

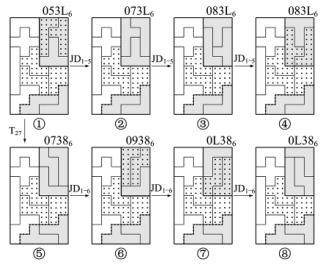
图2－24　可变换组合图形应用例3

例3　如图2－24所示，图案①053L6中右上方有由拼板5，7，8构成的矩形具有4种变换（JD1－5）。同时，拼板5，8与拼板9，L又有替代型变换T27，且与矩形变换不相干。所以经替代变换后的新矩形7，9，L同样有4种变换（JD1－6）。图案①到图案④是矩形5，7，8的变换，图案⑤到图案⑧是矩形7，9，L的变换。故该系列共有2×4＝8幅图案（见第9章〈6〉－3－3系列）。

例4　如图2－25所示，图案①6751L比较复杂。首先它的上半部由拼板0，2，6，7和9构成的图形是旋转型变换XD31－1，旋转后成图案②0751L；其次，图案②的下半部由拼板1，3，4，5，6，10和L构成（6×6－1）方式的旋转型图形XD36－19，旋转后成图案③07615；图案③中拼板4，8又构成对称型变换ZD7，变换成图案④；图案④中又有拼板2，4构成的对称型变换ZD2，变换后成图案⑤。这是一个典型的链式关联（摆式关联）变换系列。摆的两端为图案①和图案⑤，即变换由图案①到图案⑤，或由图案⑤到图案①。因为只有完成前一个变换，后一个变换才能实施。在链式关联中，4次变换产生4＋1＝5幅图案。变换中除图案①到图案②的变换外，其余3次变换都是4号拼板的变化（见第9章〈6〉－2－24系列）。

图2－25　可变换组合图形应用例4

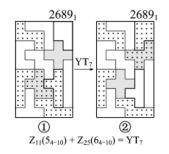
图2－26　可变换组合图形应用例5

例5　对称型（DD型、JD型、XD型和ZD型）、E型、T型等变换都是从原有图案中进行变换，使图案衍生新的图案。Z型变换也可以在同一图案中进行，但在这幅图案中要同时有两对能配对的Z型变换时方能成功。在图2－26中，图案①26891中有置换变换Z11（54－10）和Z25（64－10），实际上就是将拼板5和6都翻过来，6号拼板的正、反面可以置换拼板4与10，5号拼板的正、反面也可以置换拼板4与10。图案①经过置换后成图案②，这两幅图组成一个变换系列（见第9章〈6〉－2－112系列）。实际上Z11和Z25的联合应用已变成了隐性变换YT7。

2．5．2　由组合图形作基础，创造出新图案

若把可变换组合图形作为一个单元先拼好，放进图案中，再拼其他拼板，直至完成一幅图案，那么这个图案就是一个变换系列，可达到事半功倍的效果。

例1　如图2－27①所示，先设计两个可互相替代的拼板组合3，6和2，5，把这两组组合安放在图案的左上角和右上角，是一个阶梯形状。以后只要解决余下的8块拼板的拼搭，拼成的图案就是替代型变换T20－2系列，如图2－27②中的图案A和图案B。同时图案B中拼板1，8与6，7构成的图形又可替代，经过T30的变换成了图案C。所以这个系列有两次替代，3幅图案（见第9章〈6〉－2－88系列）。

图2－27　组合图形应用例1

例2　图2－28①是事先设定好的两个可替代的图形——拼板0，10和拼板4，6。拼图时将这两个图形置于图案的顶部。拼板4和6本身又是对称性图形（ZD6－1），所以构成2×2＝4幅图案，即图2－28②中的图案A～图案D；在图案②D中，拼板2和4又构成对称性变换ZD1，变换后成图案E。所以该系列就有2×2＋1＝5幅图案（见第9章〈6〉－2－13系列）。

图2－28　组合图形应用例2

2．5．3　隐性替代型变换有助图案最后两块拼板的拼图

隐性替代变换可以在解决图案最后两块拼板时大显身手。在隐性变换时，拼板A，B可以拼成各种图形，拼板C，D也可以拼成各种图形，只有当A，B构成的图形与C，D构成的图形的外形相同时才能互相替代，而替代出来的拼板又可拼成其他图形。所以在拼图中常利用隐性替代变换的这个性质来帮助解决图案的最后两块的难题。

例1　如图2－29所示，图案拼到最后两块余下的拼板是1和L，为便于记录，用U1，L表示，留下的空位为7，9，记为K7，9^[1]。用拼板1，L替代图案中的7，9（T33），将置换出来的拼板7和9放进空位中即成图形②的图案14675。

例2　如图2－30所示。图案最后余下拼板2，6，留下空位7，9。用拼板2，6置换出图案中的7，9（T40），而拼板7和9与空位吻合，构成图形②的图案58L71。

图2－29　隐性变换应用例1

图2－30　隐性变换应用例2

图2－31　隐性变换应用例3

例3　如图2－31所示，图案最后余下拼板3，6，留下空位1，5。拼板3，6替代1，5（T20－1），而拼板1和5正好放进空位里，构成图形②的图案39158。

2．5．4　置换型变换能帮助闯过第十二块的难关

“伤脑筋十二块”拼图时，最伤脑筋的是第十二块如何放进去。要解决这个难题，可从置换型变换（Z型）中得到帮助。

1．通过置换型变换（Z型）使余下的拼板符合留下的空位

例1　如图2－32所示，拼图中余下的拼板是4而留下的空位是8（U4 K8）。经过Z10（54－8）的置换，使留下的空位和余下的拼板相吻合，构成图案②0L631。图2－32下面的注明“U4K8→（Z1054－8）→U4K4”，表示原图形①中的U4，K8通过Z10的变换成U4，K4，拼图完成。

图2－32　置换型变换应用例1

置换型变换应用例2、例3、例4分别见图2－33、图2－34、

图2－35所示。

图2－33　置换型变换应用例2

图2－34　置换型变换应用例3

图2－35　置换型变换应用例4

2．利用T型变换与Z型变换相结合及配合奇拼板的特性攻克第十二块难关

例5　图2－36所示为5×12框图，图案拼到最后时局势为U9，K5（图形①）。经过拼板4，9与拼板5，10的替代变换T58使图形②的空位为4而余下的拼板为10（U10，K4）。再经过Z25 （64－10）的置换，最后构成图案③18975。

例6　如图2－37所示，图形①中余下8号拼板而空位为L（U8，KL）。经过T27（5，8～9，L）变换成图形②的U9，K5；再经过Z28（65－9）的置换，构成图案③的U9，K9，编码为0817L。

图2－36　置换型变换应用例5

图2－37　置换型变换应用例6

例7　如图2－38所示，图形①中为U8，K6，将5号拼板翻身并以8号拼板代替2号拼板成图形②，这时成U2，K10；将10号拼板下移成图形③，再经过Z4（42－10）置换变换成图案④的U2，K2，即图案276L8。

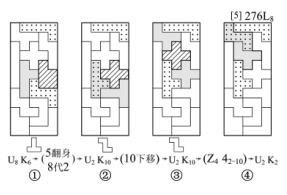
图2－38　置换型变换应用例7

2．5．5　其他变换技巧

1．有趣的连环变换

如图2－39所示，图案176L10（图形①）似乎只是个自变系列，其实不然。图形中有3个可变换的组合图形：组合A1──拼板0和4，组合B1──拼板5和6，以及组合C1──拼板8和9；与它们外形相同的组合图形有：组合A2──拼板6和8，组合B2──拼板0和9，以及组合C2──拼板4和5。这样可以形成系列替代变换，即T3－4（0，4～6，8），T15－2（0，9～5，6）和T51 （4，5～8，9）。变换中组合C1是关键。

图2－39　有趣的连环变换

变换过程如下。

先在图案①中用组合C2替代组合C1，即T51（4，5～8，9），替代后成图形②，这时空位是4、5，余块是8、9。其次，9号拼板可与0号拼板构成组合B2替代组合B1，即T16－2（0，9～5，6），替代后构成图形③，这时的空位是0，4，余块是6，8。第三次替代是T4－4（0，4～6，8），变换成图④，即新图案170L10。图案的3对组合图形，6个拼板，经过三次重新排列组合而变换成另一个新图案。

有趣的是变换前图案176L10中3对拼板的组合排列为

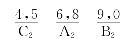
变换后图案170L10中3对拼板的组合排列变为可以看到，两组排列中拼板的次序没变，只是0号拼板的位置从首位移至末位，似乎组成一个环状，戏称“连环变换”。

在图案170L10（见图2－39④）中，有拼板6，7的对称型变换ZD5－2，变换后又有拼板6，8的旋转型变换XD3－2，所以形成了二阶变换系列。图集中变换系列编号为〈6〉－2－40。

2．拼板0，6的变换

拼板0和6是相邻的，如何把0，6调换是拼图中常常遇到的。图2－40所示为一实例。

图2－40　拼板0和6变换实例

图2－40①中有空格“0”，多余的拼板为“6”，拼图中需把空格0换成空格6以便把多余的6号拼板放入。把图形①中的拼板3，5和9取出，把5号拼板反过来放入，同时把3号拼板转个身，成图形②。在图形②的空缺部分正好可放进拼板6和9，于是完成了拼板0和6的调换。

【注释】

[1]U表示余下的拼板，下标为其拼板编号；K表示图案中的空位，下标为可以放入的拼板编号；图中用斜线条表示空位。