一切运动皆为假象

一切运动皆为假象

我们将探讨的9个悖论当中的第一个，可追溯至2500年前。经历这么长时间的琢磨，相信读者并不会讶异它已被彻底破解。不过对于初次接触的人而言，这个悖论乍听之下还是令他们晕头转向。这个谜题名为“阿基里斯悖论”（the Paradox of Achilles），又称为“阿基里斯与龟的问题”，它其实是希腊哲学家芝诺（Zeno）所提出的一系列问题之一。作为逻辑思考的范例，它其实再简单不过了。但别以为本章仅只于此；我们将深入探讨数个芝诺悖论（Zeno's paradoxes），最后以其中一个悖论的现代版作结；它仅能以量子论来解释。嘿，我从来没有说要轻易放过各位读者。

首先来看芝诺悖论当中最著名的一个：在一场与身手矫健的阿基里斯的赛跑中，乌龟被允许率先出发；当阿基里斯起跑时，乌龟已经抵达路途中的某处（姑且称为A点）。由于阿基里斯跑得比乌龟要快许多，他很快就抵达A点。然而，当他跑抵该处时，乌龟已经移动到更远的地方，我们把它称做B点。当阿基里斯跑抵B点，这时乌龟已经爬到更远的C点；这个过程不断重复。尽管阿基里斯不断追近乌龟，每个阶段两者之间的差距也不断缩小，前者却永远不可能超越后者。这个叙述错在哪里呢？不论是聪明才智、各种逻辑难题的推敲，或者仅是概括性的深刻思考，我们都无法凌驾希腊人。事实上，这些古哲学家们如此犀利，他们的逻辑具有如此深刻的洞察力，令人老是忘记他们是2000多年前的人物。时至今日，当我们想举天才的例子时，除了人气始终居高不下的爱因斯坦之外，也常提及诸如苏格拉底、柏拉图以及亚里士多德等人，作为人类智识卓越典范的代表性人物。

芝诺诞生于古希腊的埃利亚城，该城位于现今意大利西南部。我们除了知道他是埃利亚哲学家巴门尼德斯的学生之外，对其生平与著作所知皆不多。他们与另一位出身该城的哲学家麦里梭共同组成现今所称的埃利亚学派。他们的哲学思想主张，一个人不能仅仅透过感官及感官经验来理解这个世界，最终还必须依赖逻辑与数学。整体而言，这是合理的看法；不过读者将会察觉，这个理念却将芝诺引入歧途。

就我们对芝诺思想仅有的了解，他似乎少有自己原创的建设性观点，而是热衷于推翻他人的论证。尽管如此，活跃于芝诺之后100年的亚里士多德依然将他视为“辩证法”这个论证方式的创始人。辩证法是古希腊人（尤其是柏拉图与亚里士多德等哲学家）擅长的一种开放式讨论，透过逻辑与推理在讨论中解决想法意见上的歧异。

芝诺的原著当中只有一部篇幅甚短的著作流传至今，因此我们所知关于他的一切皆来自于他人的著述，特别是柏拉图与亚里士多德。芝诺于40岁左右旅行至雅典，并在那里遇见年轻的苏格拉底。他晚年活跃于雅典政坛，最终因共谋推翻埃利亚城的统治者而被捕入狱，并且刑求致死。有一则关于他的故事说，他宁愿咬掉自己的舌头吐在逮捕者的脸上，也不愿供出共谋者。但他最著名的，还是透过亚里士多德的巨著《自然哲学》（Physics） 流传后世的一系列悖论。一般相信他共提出过约莫40个悖论，但只有少数流传下来。

芝诺的所有悖论都围绕着一个中心思想：一切都是亘古不变的；运动状态只是一种假象，而时间本身并未真正存在。其中最著名的4个悖论分别被亚里士多德命名为：阿基里斯（the Achilles）、 二分法 （the Dichotomy）、运动场 （the Stadium） 与飞矢不动 （the Arrow） 悖论。如果有什么是希腊人擅长的，那当然是哲学思考了。像“一切运动皆为假象”这种恢宏的宣言，正是他们著名的抽象思考得到的结果，充满煽动性。我们可以用现代的科学方法来驳倒这些悖论，不过它们实在有趣极了，值得我们重新探讨。本章将逐一检视这些悖论，并且说明如何运用较为谨慎的科学分析来破解它们。首先从我刚刚描述过的悖论开始吧。

这是我个人最喜欢的芝诺悖论，因为它乍看之下完全合乎逻辑，却以出乎意料的方式挑战逻辑。阿基里斯是希腊神话中最伟大的战士，拥有天生神力、勇气与战斗技巧。半人半神的阿基里斯，其双亲为色萨利国王珀琉斯与海神忒提斯。在荷马描述特洛伊战争的史诗《伊里亚德》（Illiad）里，他的角色非常突出。据说当他还是小男孩时，速度已经快到足以捉住鹿，身体强壮得足以杀死狮子。

芝诺在他的悖论中选择这位神话英雄与笨重的乌龟赛跑，显然是两种极端的对比。

此悖论乃是基于更古老的龟兔赛跑寓言，出自于名叫伊索的另一位古希腊人，大约活跃于芝诺之前的100年。在原本的寓言中，乌龟遭到兔子嘲笑，因此向兔子下战帖赛跑，结果乌龟及时抵达终点而获胜。兔子过于自大，以为自己的速度快到可以在中途睡上一觉，结果却太晚醒来而追不上乌龟。

在芝诺的版本里，飞毛腿阿基里斯取代了兔子的角色。与兔子不同的是，他完全专注于比赛，却因为让乌龟率先起跑而种下败因。无论赛跑距离多长，乍看之下乌龟终将赢得比赛，尽管在古希腊人眼里两者抵达终点的顺序也许难分轩轾。根据芝诺的解释，不论这位英雄跑多快，或是乌龟爬多慢，阿基里斯永远无法超越乌龟。这显然与事实不符，究竟怎么回事呢？对于古希腊时期的数学家而言，这是个重大的难题，因为在当时还没有所谓的“无穷级数收敛”（converging infinite series）概念，甚至连“无穷大”的意义都尚不明朗（这些观念稍后会加以解释）。在当时，擅长思考此类问题的亚里士多德已经认为芝诺旳想法是一种“谬误”。问题在于亚里士多德及其他古希腊哲学家并无人知晓以下这个基本的物理学公式：速率等于距离除以时间。时至今日，我们对于物理学的了解已经比希腊人深刻许多。

“阿基里斯永远无法超越乌龟”的叙述显然不对。在以上所述的每一阶段里（A点与B点之间，接着是B点与C点之间，依序下去），逐步递减的距离同时意味着着逐步递减的时间间隔，因此无穷多个步骤并不等于无限长的时间。事实上，所有步骤加总起来得到的时间是有限的，也就是阿基里斯追上乌龟所耗的时间！这个悖论的矛盾症结在于，多数人无法接受将一串无穷长的数列累加之后，总和却不见得无穷大。有限的时间之内能够完成无穷多个步骤听来也许很怪，然而逻辑却告诉我们，乌龟可以轻易地被追上并超越。这个矛盾的破解有赖于数学家所称的“几何级数”。

考虑以下级数的例子：

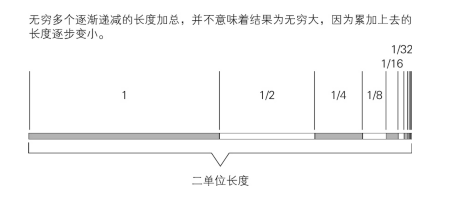
1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 ……

读者当然可以试着将愈来愈小的分数不断累加上去，使得总和愈来愈接近2。大家可以试试看，在纸上画一条直线，将它等分为两段。接着将右半段再等分为两半，继续下去直到直线小到无法在纸上做记号为止。如果取直线的一半作为一单位长度（单位用公分、英寸、公尺或英里皆可），那么将以上级数中的分数连加之后，总和将收敛于二单位长度。

如果将以上方法应用到本悖论，我们应当考虑每阶段阿基里斯与乌龟之间逐渐递减的距离，而非两者的个别位置。由于他们各自以不同的等速率前进，两者之间的距离也以等速逐渐减少。例如，假若阿基里斯让乌龟领先100公尺起跑，之后以每秒钟10公尺的速率接近乌龟，依照芝诺的讲法结果会如何呢？嗯， 5秒后两者之间的距离将会减半，再过两秒半之后再减半，再过一又四分之一秒之后再减半，如此继续下去。如果愿意的话，我们可以将这些逐步递减的时间间隔里逐步递减的跑步距离累加起来，但是并不会改变如下的事实：如果阿基里斯以每秒10公尺的速度赶上乌龟，他会在10秒钟之后超越对手，这正是他将两者之间原本100公尺的距离削减至零所需的时间。而这10秒正是无穷级数的总合：5秒＋2.5秒＋1.25秒＋0.625秒＋……累加起来，直到下一个累加的分数小到让我们愿意停下来为止（此时总和等于9.9999……秒）。 10秒钟之后，乌龟理所当然只能看着阿基里斯绝尘而去（除非阿基里斯决定在半路上停下来喝杯啤酒，但这种故事情节对芝诺澄清其论点并无任何帮助）。