组合数学初步

5.2.1　排列与组合

1772年，旺德蒙德以［n］^p表示由n个不同的元素中每次取p个的排列数。而欧拉则于1771年以和1778年以表示由n个不同元素中每次取出p个元素的组合数。1872年，埃汀肖森引入了以表相同之意，这组合符号一直沿用至今。

1830年，皮科克引入符号Cr以表示由n个元素中每次取出r个元素的组合数；1869年或稍早些，剑桥的古德文以符号nPr表示由n个元素中每次取r个元素的排列数，这用法亦沿用至今。按此法，nPn便相当于现在的n！。

1880年，鲍茨以ⁿCr及ⁿPr分别表示由n个元素取出r个的组合数与排列数；六年后，惠特渥斯以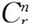及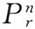表示相同之意，而且，他还以表示可重复的组合数。1899年，克里斯托尔以nPr及nCr分别表示由n个不同元素中每次取出r个不重复之元素的排列数与组合数，并以nHr表示相同意义下之可重复的排列数，这三种符号也通用至今。

1．两个基本原理是排列和组合的基础

（1）加法原理：做一件事，完成它可以有n类办法，在第一类办法中有m₁种不同的方法，在第二类办法中有m₂种不同的方法，…，在第n类办法中有m_n种不同的方法，那么完成这件事：共有N＝m₁＋m₂＋m₃＋…＋m_n种不同方法。

（2）乘法原理：做一件事，完成它需要分成n个步骤，做第一步有m₁种不同的方法，做第二步有m₂种不同的方法，…，做第n步有m_n种不同的方法，那么完成这件事共有N＝m₁×m₂×m₃×…×m_n种不同的方法。

注意区分两个原理，要做一件事，完成它若是有n类办法，是分类问题，每一类中的方法都是独立的，因此用加法原理；做一件事，需要分n个步骤，步与步之间是连续的，只有将分成的若干个互相联系的步骤，依次相继完成，这件事才算完成，因此用乘法原理。

这样完成一件事的分“类”和“步”是有本质区别的，因此也将两个原理区分开来。

2．排列和排列数

（1）排列：从n个不同元素中，任取m（m≤n）个元素，按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列。从排列的意义可知，如果两个排列相同，不仅这两个排列的元素必须完全相同，而且排列的顺序必须完全相同，这就告诉了我们如何判断两个排列是否相同的方法。

（2）排列数公式：从n个不同元素中取出m（m≤n）个元素的所有排列

排列的记号和公式为

当m＝n时，为全排列

3．组合和组合数

（1）组合：从n个不同元素中，任取m（m≤n）个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合。从组合的定义知，如果两个组合中的元素完全相同，不管元素的顺序如何，都是相同的组合；只有当两个组合中的元素不完全相同时，才是不同的组合。

（2）组合数：从n个不同元素中取出m（m≤n）个元素的所有组合的个数。

注意排列和组合的区别和联系，从n个不同元素中，任取m（m≤n）个元素，“按照一定的顺序排成一列”与“不管怎样的顺序并成一组”这是有本质区别的。

组合的记号为C（n，k）或

根据P（n，k）的定义：

4．常见计数方法

（1）特殊优先。特殊元素优先处理，特殊位置优先考虑。

【例5-4】六人站成一排，求①甲不在排头，乙不在排尾的排列数；②甲不在排头，乙不在排尾，且甲乙不相邻的排法数。

分析：①先考虑排头，排尾，但这两个要求相互有影响，因而考虑分类。

第一类：乙在排头，有P（5，5）种站法。

第二类：乙不在排头，当然他也不能在排尾，有4×4×P（4，4）种站法，

共P（5，5）＋4×4×P（4，4）种站法。

②第一类：甲在排尾，乙在排头，有P（4，4）种方法。

第二类：甲在排尾，乙不在排头，有3×P（4，4）种方法。

第三类：乙在排头，甲不在排头，有4×P（4，4）种方法。

第四类：甲不在排尾，乙不在排头，有P（3，3）×P（4，4）种方法。

共P（4，4）＋3×P（4，4）＋4×P（4，4）＋P（3，3）×P（4，4）＝312种。

（2）捆绑与插空。

【例5-5】8人排成一队，①甲乙必须相邻；②甲乙不相邻；③甲乙必须相邻且与丙不相邻；④甲乙必须相邻，丙丁必须相邻；⑤甲乙不相邻，丙丁不相邻

分析：①甲乙必须相邻，就是把甲乙捆绑（甲乙可交换）和7人排列P（7，7）×2。

②甲乙不相邻，P（8，8）－P（7，7）×2。

③甲乙必须相邻且与丙不相邻，先求甲乙必须相邻且与丙相邻P（6，6）×2×2。

甲乙必须相邻且与丙不相邻P（7，7）×2－P（6，6）×2×2。

④甲乙必须相邻，丙丁必须相邻P（6，6）×2×2。

⑤甲乙不相邻，丙丁不相邻，P（8，8）－P（7，7）×2×2＋P（6，6）×2×2。

【例5-6】某人射击8枪，命中4枪，恰好有三枪连续命中，有多少种不同的情况？

分析：连续命中的三枪与单独命中的一枪不能相邻，因而这是一个插空问题。另外没有命中的之间没有区别，不必计数。即在四发空枪之间形成的5个空中选出2个的排列，即P（5.2）。

【例5-7】马路上有编号为1，2，3，…，10十个路灯，为节约用电又看清路面，可以把其中的三只灯关掉，但不能同时关掉相邻的两只或三只，在两端的灯也不能关掉的情况下，求满足条件的关灯方法共有多少种？

分析：即关掉的灯不能相邻，也不能在两端。又因为灯与灯之间没有区别，因而问题为在7盏亮着的灯形成的不包含两端的6个空中选出3个空放置熄灭的灯。

答案：共C（6，3）＝20种方法。

5．不定方程的正整数解个数

【例5-8】求方程x₁＋x₂＋x₃＋…＋x_N＝M的正整数解的个数。

分析：想象现在有M个球一字排列，要把它们分成N组，我们用N＋1块木板将它们分割成N段，第一块木板放在第一个球之前，最后一块木板放在最后一个球之后，剩下的N－1块木板放在中间的M－1个空格中，由于每个空格中只能放一块木板，所以这是一个组合问题，答案是

又因为每一种放置木板的方法对应了一组不定方程的解，所以原问题的答案也是

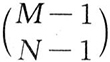
【例5-9】求方程x₁＋x₂＋x₃＋…＋x_N＝M的非负整数解的个数。

分析：设y_i＝x_i＋1，则y₁＋y₂＋y₃＋…＋y_N＝M＋N，问题转化为上一种情况。

答案：

5.2.2　几个特殊的数列

1．Catalan数

【例5-10】在一个有n＋2条边的凸多边形中，我们可以画出n－1条不相交的对角线将多边形分为n个三角形，设所有满足条件的方案数是h_n，定义h₀＝1，求h₃，h₄

分析：我们试图找出h_n的递推关系和通项公式。

考虑凸n＋2边形的任意一条边，我们设为基边，考虑这条边所在的三角形，这个三角形会把凸n＋2边形剖成两块，一块有k＋2条边（可以剖分成k个三角形），那么另一块有n＋1－k条边（可以剖分成n－1－k个三角形），根据乘法原理，这样的剖分方案数是h_k×h_n－1－k，又因为k显然可以从0一直变化到n－1（考虑边界情况，并注意到对角线不相交，所以这里不会出现重复计数），故

数列｛h_n｝就是著名的Catalan数列，在组合数学的许多问题上都有很重要的应用。Catalan数列的递推关系正如公式5.1，再加上一点生成函数的知识就可以推导出它的通项公式，但是生成函数已远远超出本书所介绍的知识范畴，有兴趣的读者可以参考其他相关内容。笔者在此给出Catalan数列的通项公式。

2．从另一种模型推导Catalan数

定理：n个+1和n个-1构成的2n项a₁，a₂，a₃，…，a_2n，并且其部分和满足

a₁＋a₂＋a₃＋…＋a_k≥0（k＝1，2，3，…，2n）

对所有k都成立的数列个数等于第n个Catalan数

证明：如果n个+1和n个-1的序列满足部分和都不小于0，则称其为可接受的，否则为不可接受的，令A_n为n个+1和n个-1形成的可接受序列的个数，令U_n为不可接受的序列个数。我们尝试计算出A_n＋U_n的值和U_n的值以得到A_n的值。

任意一个有n个+1和-1的构成的2n项必然属于且仅属于可接受序列和不可接受序列之一，于是有

下面计算出U_n的值。

对于任意一个不可接受的数列中一定存在一个最小的k，使a₁＋a₂＋a₃＋…＋a_k＜0，于是我们可以得到一些显然的结论：k是一个奇数，前k－1个数中+1和-1恰好各占一半且a_k＝－1。我们将这k个数取相反数，后面的数不变，由此得到了一个有n＋1个+1和n－1个-1的数列。注意这个操作是可逆的：对于一个有n＋1个+1和n－1个-1的数列，我们只需要找到最小的k，满足a₁＋a₂＋a₃＋…＋a_k＞0，然后将前k个数取反即可得到原数列。所以不可接受的序列和有n＋1个+1和n－1个-1的数列是一一对应的，故

再结合

可知定理成立。

3．Catalan数列的应用

因为Catalan数列满足递推关系（5.1）和定理（5.2），所以它在许多看似没有联系的模型中都有重要的应用。

【例5-11】括号序列。给出一个有n个运算符n＋1个运算数的算式，要求在算式中任意添加括号，那么本质不同的运算顺序有多少种？

分析：考虑最后一个运算的符号，它的左边有k个运算符，右边则由n－1－k个运算符，由乘法原理可知这个问题满足递推关系（5.1），于是答案是Catalan数列。

【例5-12】有2n个人排队进入剧场，入场费50元，每人都带着一张50元或100元的钞票，剧院售票处没有任何零钱，有多少种情况满足无论什么时候售票处都能找得开零钱。

【例5-13】一个n×n的网格图，从左下走到右上，每次只能向上或向右走，不能走到左下到右上的对角线的上方，一共有多少种走法？

分析：例5-12、5-13的本质是由n个+1和n个-1组成的序列中任意部分和都非负的序列总数（模型的转换希望读者认真思考），于是这两个问题的答案也是Catalan数列。

【例5-14】有n个节点的形态不同的二叉树一共有多少棵？

提示：这个问题的答案也满足递推关系（5.1）。

【例5-15】出栈序列统计，有n个数和一个栈，本质不同的合法序列一共有多少种？

提示：将一次入栈操作视为+1，一次出栈操作视为-1，剩余的分析请读者自行完成。

4．第2类Stirling数

第1类Stirling数和第2类Stirling数的出现都是基于对差分数列的研究，根据信息学初赛的要求，本书略去所有差分数列和第2类Stirling数的相关知识。下面仅仅从第2类Stirling数的一个小应用引入第2类Stirling数。

定理：第2类Stirling数S（p，k）是将p个元素的集合划分成k个不可辨认的非空盒子的划分的个数。注意，这里的不可辨认是指不能把一个盒子与另一个盒子分辨开，它们看起来都一样。

下面给出第2类Stirling数的递推关系和证明。

S（n，k）＝k×S（n－1，k）＋S（n－1，k－1）；S（n，1）＝1（n≥1），S（n，n）＝1。

上面的递推式可以用组合证明：①如果将元素1单独拿出来划分成1个集合，那么方法数是S（n－1，k－1）；②如果元素1所在的集合不止一个元素，那么可以先将剩下的n－1个元素划分好了以后再选一个集合把1放进去，方法数是k×S（n－1，k）；由加法原理得证。

5．例题

【例5-16】盒子与球。有3个一模一样的盒子和6个不同颜色的球，将这些球放到3个盒子里并且保证每个盒子里至少有1个球，求放置的方案总数。

答案：第二类Stirling数S（6，3）。

注意：Stirling数没有通项公式，只有递推求解。

5.2.3　容斥原理与错位排列问题

1．容斥原理

在计数时，必须注意无一重复、无一遗漏。为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。

【例5-17】有多少能被3或5或7整除的且小于1000的正整数？

分析：设A₁、A₂、A₃分别表示被3整除、被5整除、被7整除的数构成的集合，根据公式

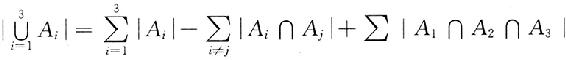
答案：

2．错位排列问题

（1）对于一个1…n的任意排列，有一种情况是第i个位置上的数不是i对任意i都能立，如n＝3时，有且仅有排列231和312是满足要求的，这样的排列被称为错位排列。

【例5-18】能否对于任意n，给出错位排列的个数？

分析：利用容斥原理。

设A_i表示i这个数在原来位置上的排列的集合，则错位排列的个数

先算∑∣A_i∣，因为有1个数在固定的位置上，有C（n，1）种情况，对于每一种情况，剩下的n－1个数任意排列，于是有C（n，1）×（n－1）！＝n！种情况。

再算∑∣A_i∩A_j∣，因为有2个数在固定的位置上，有C（n，2）种情况，对于每一种情况，剩下n－2个数任意排列，于是有C（n，2）×（n－2）！＝n！／2种情况。

……

……

一般地，因为有k个数在固定的位置上，另外（n－k）个数任意排列，所以

综上，由容斥原理，我们可以得到错位排列的公式

（2）错位排列的递推关系。考虑1号位置的那个数，不妨设为k，k＞1。有以下两种情况：

①k号位置的那个数是1，于是剩下n－2个数也是一个错位排列，有D_n－2种情况。

②k号位置的那个数不是1，那么不妨设1原来所在的位置应该在k，这样就是除k以外的n－1个数的一个错位排列，方案数为D_n－1。

最后，因为k的取值可以是2～n中的任意一个，于是我们得到了错位排列的递推关系

D_n＝（n－1）*（D_n－1＋D_n－2）

初始值D₁＝0，D₂＝1。

另一种递推关系可以由通项公式得出：D_n＝n×D_n－1＋（-1）ⁿ。

事实上，在n较小的时候，计算D_n更多的是通过递推关系而不是通项公式，但是通项公式和递推关系以及它们的推导过程希望读者能牢牢记住。

3．两个计数技巧——算两次和补集转化

（1）算两次。在对一个集合进行计数的时候，我们往往可以通过不止一条途径得到答案，那么用两种不同的方法计算得到答案应该是相同的，这样的技巧称为算两次，事实上算两次的应用并不仅仅局限于验证答案的正确性。

【例5-19】一棵二叉树中有7个节点有2个儿子，求二叉树中有多少叶子节点（没有儿子的节点）？

分析：设S表示二叉树的节点总数，S_i表示有i个儿子的节点的个数。

一方面S可以这样计算：所有节点的个数总和，即

S＝S₁＋S₂＋S₀

另一方面，S可以这样计算，根节点＋所有有1个儿子的节点的儿子个数＋所有有2个儿子的节点的儿子个数，即

S＝1＋S₁＋2S₂

两次计算结果相互对照可以得出S₀＝S₂＋1，

答案：8

这样的技巧我们可以推广到k叉树中得到更一般的结论：

S₀＝S₂＋S₃×2＋S₄×3＋…＋S_k×（k－1）＋1

（2）补集转化。在计算一个集合A中元素个数时，往往会发现直接求解很困难，但是如果利用全集C和A在C中的补集中元素的个数迂回求解一般可以达到更好的效果，这样求解的技巧称为补集转化，多用于集合本身元素个数不好分析但是全集和补集都很容易求解的情况，由于这样的情况大量存在，所以补集转化思想是一个很重要的计数技巧。

计算中用到补集转化的例子比比皆是，上文求解错位排列的通项公式时就用了补集转化的思想。第5.2.2中“从另一种模型推导Catalan数”部分，可接受序列A_n的个数不好求，但是A_n＋U_n的值和U_n的值都可以很方便地求到，于是我们利用补集转化的技巧得到了A_n的值。

5.2.4　鸽巢原理

1．鸽巢原理

鸽巢原理又名狄利克雷抽屉原理、鸽笼原理。其中一种简单的表述法为：若有n个笼子和n＋1只鸽子，所有的鸽子都被关在鸽笼里，那么至少有一个笼子有至少2只鸽子。另一种表述法为：若有n个笼子和kn＋1只鸽子，所有的鸽子都被关在鸽笼里，那么至少有一个笼子有至少k＋1只鸽子。

2．鸽巢原理的加强形式

令q₁，q₂，…，q_n为正整数，如果将q₁＋q₂＋q₃＋…＋q_n－n＋1个鸽子放入n个笼子里，那么，或者第1个笼子至少有q₁个鸽子，或者第2个笼子至少有q₂个鸽子，……，或者第n个笼子至少有q_n个鸽子。若有n个笼子和kn－1只鸽子，所有的鸽子都被关在鸽笼里，那么至少有一个笼子至多只有k－1只鸽子。

3．鸽巢原理的简单应用

【例5-20】一位国际象棋大师有11周的时间备战一场锦标赛，他决定每天至少下一盘棋，但为了不使自己过于疲劳他还决定每周不能下棋超过12盘，证明存在连续的若干天，期间这位大师恰好下了21盘棋。

证明：令a₁表示第1天所下的盘数，a₂表示前2天所下的盘数，a₃表示前3天所下的盘数……由于每天都要下至少一盘棋，故数列a₁，a₂，a₃，…，a₇₇是一个严格递增的序列。

此外，a₁≥1，而且由于每周下棋最多是12盘，即a₇₇≤12×11＝132。因此，我们有

1≤a₁＜a₂＜a₃＜…＜a₇₇≤132

此外，序列a₁＋21，a₂＋21，a₃＋21，…，a₇₇＋21也是一个严格递增的序列：

22≤a₁＋21＜a₂＋21＜a₃＋21＜…＜a₇₇＋21≤153

于是，这154个数

a₁，a₂，a₃，…，a₇₇，a₁＋21，a₂＋21，a₃＋21，…，a₇₇＋21

中的每一个都是1～153的整数。根据鸽巢原理，它们中间有两个是相等的。既然a₁，a₂，a₃，…，a₇₇中没有相等的数，并且a₁＋21，a₂＋21，a₃＋21，…，a₇₇＋21中也没有相等的数，因此必然存在一个i和一个j使得a_i＝a_j＋21。从而，这位国际象棋大师在第j＋1，j＋2，j＋3，…，i天这段时间内一共下了21盘棋。

【例5-21】（2010年全国青少年信息学奥林匹克分区联赛初赛提高组问题求解）记T为一队列，初始时为空，现有n个总和不超过32的正整数依次入列。如果无论这些数具体为何值，都能找到一种出队的方式，使得存在某个时刻队列T中的数之和恰好为9，那么n的最小值是＿＿＿。

分析：组合数学题目的一种常见思路是先猜测答案再证明。我们试图通过鸽巢原理猜出答案。

设S_i表示前i个数的和，并规定S₀＝0，事实上原题要求出最小的n，使得存在0≤i＜j≤n满足S_j＝S_i＋9。于是我们可以把S数组看做鸽子，用不能同时取的一组（即差为9）的集合构造笼子，构造方法如下：一共有18个集合按如下方式选取，｛0，9｝、｛1，10｝、｛2，11｝、｛3，12｝、｛4，13｝、｛5，14｝、｛6，15｝、｛7，16｝、｛8，17｝、｛18，27｝、｛19，28｝、｛20，29｝、｛21，30｝、｛22，31｝、｛23，32｝、｛24｝、｛25｝、｛26｝。根据题意，我们一旦在某个集合中取了两个元素，那么一定存在某个时刻队列T中数之和恰好为9，于是由鸽巢原理我们可以知道n＝18（S数组有19个元素）一定满足条件。

下面我们来证明n＝17不可行，事实上只要构造出一组不合法的序列即可。可以选择如下不合法的序列：1　1　1　1　1　1　1　1　10　1　1　1　1　1　1　1　1。

答案：n的最小值为18。

5.2.5　Nim取石子游戏

1．最简单的取石子游戏

【例5-22】有一堆石子，共n个，两个人轮流取石子，每次最少取1个，最多取m个，取完最后一个石子的人获胜，问先手有没有必胜方案。

分析：这是一个非常经典的题目，相信大部分读者都做过这样的题目。答案是：当n mod（m＋1）＝0时，先手必败；否则先手必胜。必胜策略是每一次都取走当前石子数mod（m＋1）的值。

2．SG函数

现在我们来考察例5-22的策略为什么是对的。

首先说明必败态和必胜态的概念。必败态是说当前这个状态，先手无论如何操作都必败；必胜态则是说当前这个状态，先手无论如何操作都必胜。注意，在一般确定操作状态（如不会有每次给一个随机数根据随机数操作的情况）的组合游戏中，只会存在这两种状态，如果先手和后手都足够聪明，不会出现介于必胜态和必败态之间的状态。

一个重要的性质：从必败态走到的每一个状态都是必胜态，从必胜态操作一步走到的所有状态中至少有一个是必败态。规定无法操作的状态为必败态。

在最简单的取石子游戏中，设f［N］表示还剩N个石子的状态，那么显然f［N］可以转移到f［N－1］到f［N－M］，这里面只要有一个必败态f［N］就必胜，否则必败。一点小小的递推技巧可以知道上述的必胜策略是正确的。

那么是否可以不通过递推的方式判断必胜态还是必败态呢？下面引入SG函数。

SG函数的规定如下：最终状态（不可操作状态）的SG函数为0，其余状态的SG函数规定为所有不等于它的某一个后继状态的SG函数的最小非负整数。例如，一个状态有2个后继状态，它们的SG函数分别为2和3，则当前状态的SG函数为0；2个后继状态的SG函数分别为0和2，则当前状态的SG函数为1。

SG函数判断状态是否必胜的规则是如果当前状态的SG函数为0，则当前状态必败，否则当前状态必胜。容易发现引入SG函数后我们之前递推判断必胜必败的规则也可用于SG函数的递推上。往往可以找到一些状态和SG函数之间的规律，从而避免递推。

【例5-23】（2010年全国青少年信息学奥林匹克分区联赛初赛　提高组阅读程序第3题）

输入：16

输出：＿＿＿＿

分析：这个程序实际上就是通过递推的方式来求最少取1个石子、最多取5个石子的博弈游戏的SG函数。我们可以分析出规律：状态f［N］的SG函数＝n mod 6，因此应该输出4。

4．Nim取石子游戏

现在有若干堆石子，两人轮流操作，每人每次可以从任意一堆中取任意多个，但是不能不取，取完最后一个石子的人获胜（即无法再取的人就输了）。这个问题就是最经典的Nim取石子问题。

我们在此不加证明地直接给出这个游戏状态的SG函数。

对于一个状态，设有N堆石子，每堆个数分别为a₁，a₂，a₃，…，a_N那么这个状态的SG函数为a₁ xor a₂ xor a₃ xor…xor a_N。根据SG函数的定义，a₁ xor a₂ xor a3 xor…xor a_N＞0的状态为必胜态，否则为必败态。

在这里笔者仅仅给出一个每个状态的SG函数不会等于其任意一个后继状态的SG函数的证明，更详细的关于SG函数为什么等于所有数xor值的证明见下文相关内容。

xor函数是一个可逆函数（所谓可逆函数，就是存在反函数的函数），并且它的反函数就是它本身。

举一个简单的例子，如果c＝a xor b，那么一定有b xor c＝a和a xor c＝b。

下面用反证法进行证明。假设存在一个状态的SG函数和它的一个后继状态的SG函数相等，设k＝a₁ xor a₂ xor a₃ xor…xor a_N，当前的操作是在第M堆中取若干石子，设s＝k xor a_M，即除a_M以外其他所有数的xor值，设在a_M这一堆中取走了x个，因为当前状态和这个后继状态SG函数相等，则有s xor a_M＝s xor（a_M－x）＝k，由于xor函数的反函数就是它本身，于是可知a_M＝a_M－x，从而x＝0，与游戏者不能不取的条件矛盾，故原命题成立。

5．Nim取石子游戏的必胜态策略分析

由上一部分的证明可以看出，如果有一个状态的SG函数为0，那么它的任何后继状态的SG函数一定不为0，也就是说它的任何后继状态都是必胜态，现在我们只需要找出一个方案，使得任何一个必胜态依此操作后都会形成一个必败态。

考虑任意一个必胜态的SG函数值s，将它写成二进制的表示，找出最高位的一个1。因为这一位是1，又由xor函数的运算规则可知，至少有一堆的石子数写成二进制之后这一位也是1，不妨设是第k堆，有x个石子。设x′＝x xor s，由xor函数的性质可知，用x′代替x作为第k堆的石子数之后，所有石子堆的石子数xor的值为0，于是我们只需证明x′＜x。事实上因为s的最高位的1，不妨设为第c位，由xor函数的运算规则和x这一位也是1的约定可知：x和x′在比c更高的数位上数字完全相同，且x第c位为1，x′的第c位为0，所以我们甚至无需继续比较就可以得出结论：x′＜x。

按照如上的构造方法，在第k堆中取走x－x′个石子就可以使一个必胜状态变成必败状态，于是必胜策略的可行性得证。另一方面，可以由类似的构造方法从一个SG函数为s的状态中取走某一堆中的若干石子变为一个SG函数为s′的状态，s′可以为任意一个小于s的正整数。

【例5-24】（2007年全国青少年信息学奥林匹克分区联赛初赛　普及组问题求解）现有5堆石子，石子数依次为3，5，7，19，50，甲乙两人轮流从任一堆中任取（每次只能取自一堆，不能不取），取最后一颗石子的一方获胜。甲先取，问甲有没有获胜策略（即无论乙怎样取，甲只要不失误，都能获胜）？如果有，甲第一步应该在哪一堆里取多少？请写出你的结果：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

分析：首先我们来看第一个问题，判断当前这个状态是否是必胜态。

因为3 xor 5 xor 7 xor 19 xor 50＝32＞0，所以当前的状态是必胜态，先手有必胜策略。

根据上一部分的策略，先看32的最高位，最高位为6，而石子的个数中，50的第6位为1，于是我们应该让那一堆剩下50 xor 32＝18个石子，即从50那一堆中取走32个。

5.2.6　图论浅谈——二分图理论与Ramsey理论

1．二分图

二分图又称二部图，是图论中的一种特殊模型。设G＝（V，E）是一个无向图，如果顶点V可分割为两个互不相交的子集（A，B），并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集（i in A，j in B），则称图G为一个二分图。

二分图最著名也是最重要的一个应用就是最大匹配，但最大匹配与初赛无关，我们来看另一个也很重要但是往往容易被忽视的结论：一个图是二分图的充分必要条件是这个图中不含奇环。

充分性是说如果一个图不含奇环，那么这个图是二分图；必要性是说如果一个图是二分图那么这个图一定不含奇环。

另一个显然的事实是，如果二分图的某一类点有x个，另一类点有y个，那么这个二分图中最多有xy条边。

2．例题

【例5-25】（2010年全国青少年信息学奥林匹克分区联赛初赛　提高组问题求解）无向图G有7个顶点，若不存在由奇数条边构成的简单回路，则它至多有＿＿＿＿条边。

分析：由条件可知这个图是一个二分图，设某一类点有x个，那么另一类点有（7－x）个，原题即求x（7－x）的最大值，其中x是正整数。可以用一元二次方程的性质或者一些经典的不等式得到答案为12。

我们将这个题目推广开去，如果一个图有N个点，不存在由奇数条边构成的简单回路，则它至多有条边。

注意：如果我们用一个看似更松一点的约束条件：这个图中不存在三角形，那么这个问题的答案并不会增加，取等号的条件也不变，仍为一个一类点有个、另一类点有个的完全二分图。

2．从三元环到完全子图——Turán定理^〔1〕

现在证明一个有N个点的图不存在三角形，那么这个图中至多有条边。

证明：对于一个n个点的图，有一个点x的度数最大，不妨设为b。x和b个点相连，为了保证无三角形，那么这b个点内部无边，只可能和外部有边。于是得到总边数

把这个问题推广一下，如果一个有N个点的图中不存在一个K_r＋1和更高阶的完全子图（注：K_n表示一个有n个点的完全图），那么这个图中最多能有多少条边？

Turán定理（图兰定理）回答了这个问题，由匈牙利数学家Paul Turán在1941年发现。Turán定理的内容如下：设G为K_n的子图，而G不含完全图K_r＋1。则G最多有

条边。

证明：我们对r进行归纳。r＝2的基础已证，下面我们假设r＜k时定理成立，考虑r＝k的情形（k≥3）。

设n个点最多存在r团（即完全子图K_r）的最大边数为g（n，r）。

对于一个n个点的图，有一个点x的度数最大，不妨设为b。x和b个点相连，为了保证无r＋1团，那么这b个点内部不存在r团。于是得到总边数

这是一个关于b的二次函数，当时这个函数取到最值。

把代入，得

也就得到了

综上，由归纳假设及r＝2的基础可知Turán定理成立，证毕。

4．Ramsey理论简介^〔2〕

记K_n表示n个点的完全图。

Ramsey问题：如果将一个完全图中的边染成两种不同的颜色，保证能至少存在一种颜色的K_n或存在另一种颜色的K_m（即如果不存在某一种颜色的K_n，则一定出现另一种颜色的K_m），这个图的顶点数至少为多少？（记这个最少的顶点数为r（n，m））

一个更普遍的形式是：6个人中必定存在3个人两两互相认识或两两互相不认识。事实上5个人是可以既不存在3个人两两互相认识也不存在3个人两两互相不认识的于是我们可以得出结论r（3，3）＝6。

首先我们来证明这个结论。

在6个人中，任取一个人X，考虑他和其他5人的关系。由鸽巢原理我们可以知道，这5人中他一定认识3人或不认识3人。不妨设他认识3人，设为A、B、C三人。在A、B、C这三人中如果有2人两两认识，不妨设为A、B，那么A、B、X三个人两两认识；如果不存在2个人两两认识，那么A、B、C这3个人两两都不认识，于是命题得证。

5个人中可以既不存在3个人两两互相认识也不存在3个人两两互相不认识的例子请读者自行构造，这一步还是比较简单的。

Ramsey定理：对于任意的正整数n，m＞2，r（n，m）唯一确定且有限。唯一确定是显然的，我们只需证有限。

更进一步，我们只需证到如下不等式成立：r（n，m）≤r（n－1，m）＋r（n，m－1），以及如下等式成立：r（2，n）＝r（n，2）＝n，则可以证明r（n，m）是有限的。

下面证明r（n，m）≤r（n－1，m）＋r（n，m－1）。记A＝r（n－1，m），B＝r（n，m－1）。

考虑一个有A＋B个点的图，边染为红绿两色。

任取一个点P，与这个点相连的边有A＋B－1条。根据鸽巢原理，其中必有红色的边至少A条，或绿色边至少B条。不妨设有A条红色边，考虑连到的A个点，因为A＝r（n－1，m），所以这A个点构成的子图中必存在红色K_（n－1）或存在绿色K_m；若存在红色K_（n－1），由于这n－1个点都与P以红边相连，于是加上P形成红色K_n。所以P和这A个点构成的子图中必存在红色K_n或存在绿色K_m。如果有B条绿色边同理。因此A＋B个点的图中一定存在红色K_n或存在绿色K_m，即（n，m）≤r（n－1，m）＋r（n，m－1）。证毕。

再证明r（2，n）＝r（n，2）＝n。首先一个n个点的图中要么所有边都是同色构成单色K_n，要么至少含有一条另一种颜色的边构成单色K_2，其次一个单色K_（n－1）中既不含这种颜色的K_n，也不含另一种颜色的K_2，于是r（2，n）＝r（n，2）＝n。

用简单的递推或数学归纳法可以证明r（n，m）有限。事实上我们可以得出：

综上，Ramsey定理得证。

但是确定Ramsey数的值是一个非常困难的事，目前已确定的Ramsey数很少。

Ramsey问题的推广（Ramsey定理的一般形式）。

假设正整数p₁，p₂，…，p_n，t满足p₁≥t，p₂≥t，…，p_n≥t，则一定存在一最小正整数R（p₁，p₂，…，p_n；t）满足下面性质：假设集合S至少有R（p₁，p₂，…，p_n；t）个元素，任意将其t元素子集分成n类，则必有某一i（1≤i≤n）使得S有一恰含pⁱ个元素的子集T，其所有t元素子集都是第i类。

利用上述定理的符号，则上述6人中3人互相认识或不认识的事情，就可以写成R（3，3；2）＝6，因为有6个元素的集合S的所有二元子集（一个二元子集中的两个元素可以看做一条边的两个端点，于是边的本质就是是一个二元子集）分成2类，则S必存在一个三元子集，其所有二元子集都是第一类或存在一个三元子集，其所有二元子集都是第二类。也就是说6人中必存在3人互相认识或存在3人互相不认识。

5.2.7　从两个形似的问题看数学模型的构建

本节讨论第5.1.4节中遗留下未解决的两个模型：最小任意交换排序和最小相邻交换排序。同时，本节将是组合数学部分也是整个初赛基础部分的最后一节，笔者将在最后给出一些分析数学问题和建立数学模型的建议。

1．最少任意交换排序

【例5-26】（2008年全国青少年信息学奥林匹克分区联赛初赛普及组单项选择题）将数组｛8，23，4，16，77，-5，53，100｝中的元素按从小到大的顺序排列，每次可以交换任意两个元素，最少需要交换（　　）次。

A．4

B．5

C．6

D．7

分析：初看此题，毫无头绪，我们不妨从最简单的贪心和模拟开始，看能否找到一点思路。

首先第一个数是8，排好序后第一个数应该是-5，于是做一次交换；第二个数是23，排好序后应该是4，于是做一次交换。此时序列变成｛-5，4，23，16，77，8，53，100｝。然后再把23和交换，77和3交换，77和3交换即可排好序，一共用了5次交换。我们用了贪心的思想做到了正确答案5，但目前我们还不知道这个答案为什么是对的。为此需要引入置换的概念。

设X是一个有限集。不失一般性，取X＝｛1，2，3，…，N｝，X的一个置换i₁，i₂，i₃，…，i_N是一个1到N的排列，这个置换可以视为X到其自身定义的一个一对一的函数f：X→X。其中f（1）＝i₁，f（2）＝i₂，…，f（N）＝i_N，用行列式可以表示为

事实上，如果我们把k和i_k之间连一条有向边，那么一个置换可以用一个有向图唯一地表示。特别地，这个有向图是由一些有向环组成的（包括只有一个点的自环），注意到我们每次交换两个元素只有当这两个元素在一个环上时才有意义，并且一个有k个点的环至少需要交换k－1次才能完成排序。因此最少任意交换排序的答案即N－置换环的个数。

2．最少相邻交换排序

【例5-27】改变例5-24的条件，每次只能交换两个相邻元素，最少交换次数是多少？

分析：例5-24和5-25看上去很相似，但它们只是形似，本质的数学模型毫无相近之处。

为解决这个问题，我们先考察相邻交换的性质。注意到相邻交换只会改变相邻两个数的相对大小而不会影响到别的数，因此我们考虑能不能从改变相对大小这个方面入手。在数列中，有一个值和相对大小密切相关，那就是逆序对数。所谓逆序对，就是指一个数列中的两个数i和j，i在数列中的位置在j的前面并且i＞j。显而易见的是，一个排好序的数列的逆序对数为0。现在我们看看相邻交换对逆序对数有什么影响，如果前一个数小于后一个数，交换后逆序对数加1；否则逆序对数减1。因为排好序的数组不含逆序对，所以我们希望逆序对数减得尽量快，这样可以尽可能减少交换次数。而另一方面，对于一个没有排好序的数组，我们一定可以找到两个相邻的数是逆序对，这样当逆序对数大于0的时候，我们总可以通过一次交换使逆序对数减1。于是最小相邻交换排序的交换次数就等于原数列的逆序对数。

3．浅谈组合数学问题分析中数学模型的构建

（1）尝试，或者说探索，这是一个很重要的步骤，我们可以用模拟、贪心等各种手段来探索问题的解，很可能这一步得到的答案甚至不需要进行后续的分析。

（2）从小数据入手，分而治之。很多题目把数据规模改小之后和原题的处理方法是差不多的，这一点可以在第（1）步探索时试出来。

【例5-28】（2006年全国青少年信息学奥林匹克分区联赛初赛　普及组问题求解）现有80枚硬币，其中有一枚是假币，其重量稍轻，所有真币的重量都相同，如果使用不带砝码的天平称重，最少需要称几次，就可以找出假币？你还要指出第1次的称重方法。请写出你的结果：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

分析：80这个数据规模很大，我们不妨从小数据入手。如果有2枚硬币，只有1枚假币，那么很显然一次称重就可以；3枚硬币也是1次就可以（天平的两边各放一枚）。3枚以上的可以分成3堆，其中两堆数目相同，然后把两堆相同数目的放到天平上称重，这样一次我们就可以知道假币在哪一堆中，然后这个问题就被用一次称重转化到数据规模为原来1/3的问题了，于是原问题的答案是［log3N］＝4。

（3）分析题目中的有效信息，准确地说，是找到题目中的“特点”，如计数时的一些限制，最少交换排序的交换方式，这些题目特有的性质是我们分析的要点。

（4）构建有效的数学模型。这是最重要的一步，但事实上一般的考试题目是没有必要进行严格分析的，第（1）步和第（2）步往往已经可以解决问题。模型的构建是和题目密切相关的，也就是根据题目的特点构建的。比如最小相邻排序问题中，我们需要寻找一个量，使得交换相邻两个数时，这个量的变化是确定的，这样逆序对数就给我们提供了一个恰当的帮助。

数学问题是千变万化层出不穷的，我们也无法给读者提供一个能解决所有问题的方法，希望能给读者一些思维方法和分析问题上的启迪，起到抛砖引玉的作用。是要想真正做好数学题，仅靠这一点知识基础是不够的，希望读者能寻找到一些合适的题目多加练习。

注　释

〔1〕本内容仅供有兴趣的读者参考，不要求读者熟知这个定理和它的证明

〔2〕本内容难度很大，供有兴趣的读者参考