一、宁波现代海洋产业选择的评价方法
以实际数据为基础,采用合理的评价指标,应用科学的计算方法对现代海洋产业进行定量分析与选择是至关重要的。考虑到海洋经济统计数据有限,没有典型分布规律的特征,同时尽可能避免主观判断的影响,笔者拟采用层次分析法、灰色聚类方法进行分析,对宁波市海洋经济的主导产业选择进行实证分析,旨在准确、巧妙地找出主导或优势因素。
(一)指标综合
评价指标确立以后,接着需要解决如何将单个指标的评价结果化成一个能反映综合水平的评价结果,而且最好是一个量化的、可比较的数值。具体的处理方法有很多种,这里我们采用层次分析法,把竞争力评价的各个指标先化为无量纲的分值,即量化测度,再得出一个容易比较的、量化的结果,能够直观显示海洋产业综合效益的大小。
1.层次分析法
层次分析法(Analytic Hierarchy Process,简称AHP)是由美国著名的运筹学家、匹兹堡大学教授T.L.Saaty最早提出来。层次分析法在本质上是一种决策思维方式,它把复杂的问题分解成各组成因素,将这些因素按支配关系分组以形成有序的递阶层次结构,通过两两比较判断的方式确定每一层次中因素的相对重要性,然后在递阶层次结构内进行合成以得到决策因素相对于目标重要性的总顺序。层次分析法体现了人们决策思维的基本特征:分解、判断、综合,具有系统性、简洁性、灵活性、实用性等特点,是进行评价、决策、计划和系统分析的简单而实用的方法。该方法作为一种定性与定量相结合的工具,目前已在油价规划、教育计划、钢铁工业未来规划、效益成本决策、资源分配和冲突分析等方面得到广泛的应用。
同样,我们可以利用层次分析方法来确定海洋产业选择中各因素的权重,以Xp1,Xp2,…,Xpn作为现代海洋产业选择的二级指标,以C1,C2,…,Cn作为一级指标。通过计算得出各二级指标的量化测度,利用层次分析法对二级指标进行计算得出一级指标的量化测度,再对一级指标利用层次分析法得出一级指标的值并进行综合分析,得到的结论就是我们需要的结果。其计算过程的拓扑结构如图3-7。
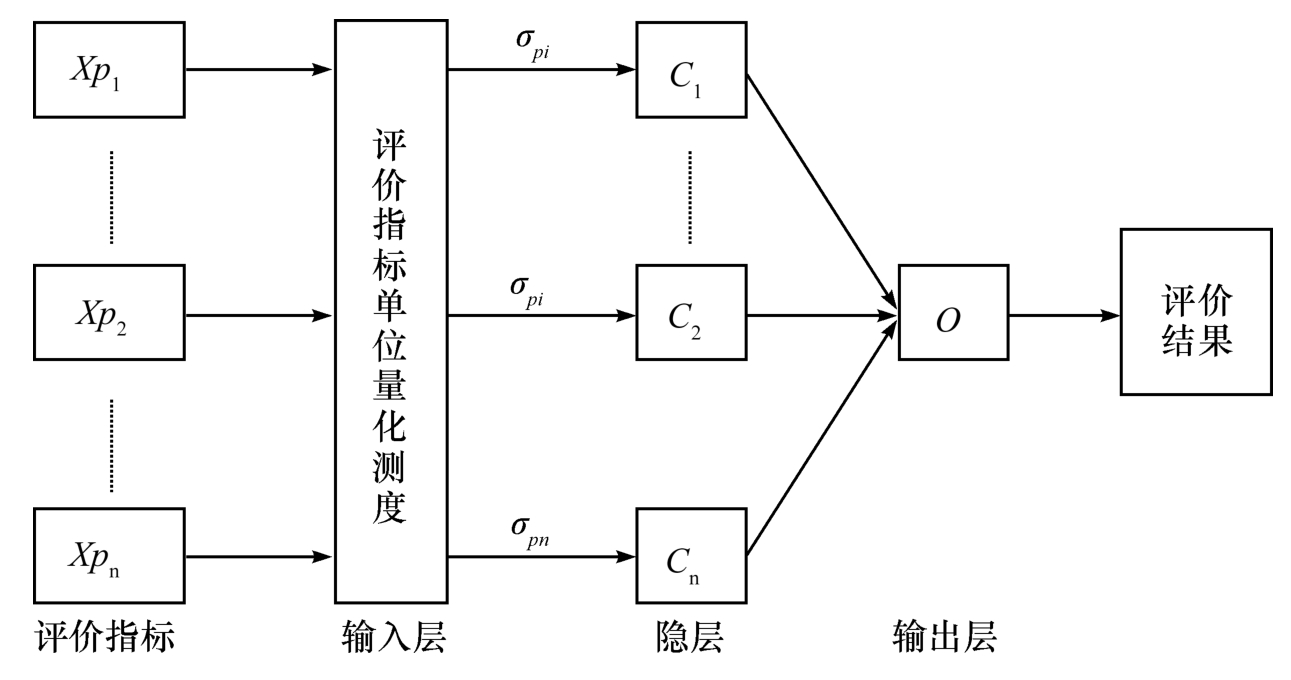
图3-7 层次分析法
2.确定各项指标的权重
采用专家德尔菲法,由九位专家对各项指标的重要性权重作出判断,确定操作层具体指标体系在其对应的第二子层评价因素中的权重,并且总权值等于1;然后,对每个第二子层评价因素予以分值,取加权平均计算出各个第二子层评价因素的分值,为以后的模型所用。计算公式如下:
![]()
其中,W ik为第i个一级指标中第k个二级指标的权重;Zik为第i个一级指标中第k个二级指标的量化测度;W i为第i个指标的权重;n为一级指标数,本评价指标体系中n=5;m为一级指标所含的二级指标数。
(二)最终的指标体系
详见表3-5。
(三)评价方法
1.无量纲化处理
评价体系是由不同统计指标构成的综合评价指标体系。因此,在计算综合评价指数的过程中,数据必须进行无量纲化处理,即通过对各指标数据进行标准化处理,以消除量纲,将其转化为无量纲、无数量级差别的可以进行比较和运算的标准分值。无量纲化有多种方法,考虑到直观性、简单性和可行性等因素,我们采取标准化方法消除数据量纲的影响。标准化公式为:
![]()
其中,xj表示宁波市第j个海洋产业统计指标统计值,xmax和xmin分别表示宁波各海洋产业对应统计指标中的最大值和最小值,yj表示无量纲化后第j个海洋产业的统计指标值。
2.评价方法
我们采用线性加权法对评价目标进行综合评价。反映第i个海洋产业总评价目标的评价公式为:
![]()
其中,W j表示第j项统计指标的权重,W j满足∑jW j=1,0<W j<1;Ui表示第i个海洋产业的综合评价指数。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















