统计学错误

统计学分析可分为描述性和推断性统计两大类。描述性统计用于描述数据的分布特征和规律，如均数、标准差、中位数、率、构成比等；推断性统计用于比较组间差异，如t检验、方差分析、χ2检验、秩和检验等，或探讨相关因素，如相关分析、多元回归分析等。现将护理论文中常见的统计学错误列举如下。

（一）对P值的含义描述不恰当

在统计学中，把P＜0.05或P＜0.01视为小概率事件，是事物差别有统计学意义的界限。但P值的大小只说明统计学意义上“显著”，不说明临床意义上实际差别“显著”，也不应把P＜0.05或P＜0.01误解为差别很大。为了避免统计“显著”与专业“显著”混淆，在描述P值时，最好用“差异有或无统计学意义”，避免用“差异有或无显著性”。此外，统计结论是根据P值大小得出的，P值越小，抽样误差发生的可能性越小，但“小概率”事件不代表绝对不可能发生，统计结论也有犯错误的概率。所以，在根据P值下结论时要慎重，应结合专业知识去分析，尽量不用过于肯定的语言。

（二）未做统计学分析，仅凭数值大小下结论

在抽样研究中，样本与总体之间会有差值存在，即抽样误差，因此，从样本所得到的数值上的差异或相关，可能由抽样误差所致，而非总体之间本质上的差异或相关。所以，要得出有无差异或相关的结论，必须进行推断性统计分析，以判断这种差异或相关是来源于抽样误差，还是本质存在。而有些论文未做统计学分析，仅凭样本数值上的差异就得出总体有无差异的结论。例如，某作者由“两组有效率分别为89.2%和61.7%”，得出“A组明显高于B组”的结论，这显然不科学，应进行χ2检验，若P＜0.05，才能得出该结论。

（三）统计学分析方法交待不清

为了便于对结果进行核对和二次评价，以判断其真实性和科学性，在描述结果时，应明确采用的是何种统计学分析方法，并列出相应的统计量值（如t值、F值、χ2值）及其相应的P值。而在有些论文中，常出现“经统计学处理，差异有统计学意义（P＜0.05）”这样的描述。由于作者并未明确采用的统计学分析方法，也未列出具体的统计量值，因此无法判断该研究中的统计学分析方法是否正确，也就无法判断结果是否正确、可靠。

（四）率和构成比混淆

构成比只能说明事物各组成部分的比重或分布，并不能说明某现象发生的频率。例如，某护士调查所辖社区慢性病患者的年龄分布情况，结果见表3-2。表中的构成比仅说明，在患有该病的人群中，各年龄段所占的比重，而不能将其看作各年龄段该病的患病率，或得出41～59岁组患病率最高的错误结论。

表3-2　某病各年龄段分布情况

（五）偏态分布的资料以正态分布对待

正态分布的资料可用均数和标准差来描述，采用t检验、方差分析等方法；而偏态分布资料则用中位数和四分位数间距描述，采用秩和检验的方法。原则上，需先进行正态分布检验，以判别资料的分布类型。但粗略来说，可从标准差和均数的大小关系上进行粗略判断：当标准差×2≥均数时，应怀疑是否为偏态分布。在护理论文中，常出现下列情况：“工作年限为3.1±4.3年”，该例中，标准差×2明显大于均数，因此，应写出中位数。同样，也有论文中对偏态分布的资料仍采用t检验，这种做法不妥。

（六）误用t检验代替配对t检验

当研究设计为自身对照时，应采用配对t检验进行统计分析。例如，某研究采用自身对照，在同一人身上，同时采用耳温仪和水银体温计测量体温，欲比较两种方法测得的体温值是否有差异。该例应采用配对t检验进行分析，而作者却采用了两个独立样本t检验，这样做会加大犯二类错误的概率，即可能把本来有差异的两个均数判断为无差异。

（七）方差分析时不进一步做两两比较

当方差分析的结果为P＜0.05或P＜0.01时，只说明各组间均数不全相等。若想进一步了解每两组之间是否存在差异，需进一步做两两比较。但在有些论文中，有研究者单凭F值就得出哪两个组之间有差异的结论（表3-3）。

表3-3　不同学历护士疼痛得分比较（x±s）

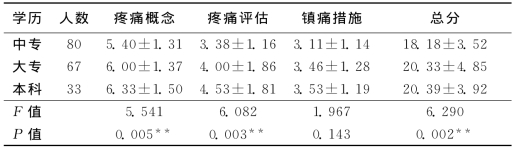
由表3-3可见，不同学历护士疼痛知识总分及疼痛概念、疼痛评估得分存在统计学差异，学历越高，得分越高。

该例中，经方差分析得出P＜0.01，只能说明不同学历的护士疼痛知识得分不同，但无法得出哪两组不同。本文作者未进行多个样本均数的两两比较，就直接得出“学历越高，得分越高”的结论，这样缺乏科学依据。

（八）χ2检验时不注意各公式的适用条件

χ2检验适用于两组或多组率或构成比的比较。其计算公式分为专用公式、校正公式、确切概率法几种情况，各有其适用条件。以四格表χ2检验为例：

（1）当总例数N≥40，且所有格子的理论数T≥5时，用四格表专用公式：

（2）当N≥40，但有格子的理论数1≤T＜5时，用四格表校正公式：

（3）当N＜40，或有T＜1时，用Fisher’s确切概率法。

采用计算机软件进行分析时，输出结果会给出有关理论值大小的备注，应根据具体情况选择相应的公式。而在有些论文中，研究者不注意各公式的适用条件，则可能导致相反的结果（表3-4）：

表3-4　两种方法消毒后合格率比较

注：χ2＝4.645，P＜0.05

在表3-4中，实际数最小的格子“1”所对应的理论数为T1＝46×8／94＝3.91，在1～5之间，故宜选用校正公式。如果将各数值代入校正公式，计算可得χ2＝3.188，P＞0.05。而作者却采用了专用公式计算，得出了相反的结果。

（九）不注意相关分析的适用条件

在进行相关分析时，当两个变量均为计量资料、且符合正态分布时，可采用Pearson相关；当两个变量为等级资料或不服从正态分布时，宜采用Spearman等级相关；而当其中一个变量为计数资料时，此时不宜用上述方法计算相关性。例如，欲探讨“是否计划怀孕与产后抑郁发生率之间有无相关性”，研究者仍采用相关分析的方法，这样做不妥。此时，可将其转化为“计划怀孕和非计划怀孕这两组产妇抑郁发生率是否有差异”这个问题，进行χ2检验。若得出P＜0.05，可认为“是否计划怀孕与抑郁发生率存在关联性”。然后，可通过下列公式，进一步计算Pearson列联系数，以得出相关的程度：

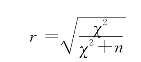
（十）相关分析结果报告不恰当

在进行相关分析时，计算出r值后，需对其进行假设检验，以判断这种相关是本质存在，还是由抽样误差所致。因此，在报告结果时，应同时报告r值和P值。P值代表两变量之间在统计学意义上是否存在相关，r值则代表相关的方向和程度。例如：由“r＝－0.127，P＞0.05”的结果，可得出“二者无相关性”的统计结论，而有研究者将其描述成“二者呈负相关，但无统计学意义”，这种描述是错误的。再如：由“r＝0.456，P＜0.01”的结果，可得出“二者呈中度正相关”的统计结论，而有研究者看到P＜0.01，而不看r的大小，将其描述成“二者呈高度正相关”，这也是错误的。