文献中能够查到的N-S方程的解析解只有几十个。这些解虽然为数不多,却在相当程度上揭示了粘性流动的本质特征,其中有些解也具有重要的应用价值。在发展新的数值计算方法时,可以运用有解析解的算例来判断近似解的精确程度;在复杂的粘性流动问题中,可以用情况相近的解析解作为初步估算或者摄动法的求解基础;在研究某些新问题时,也常常从解析解出发,探讨在原有方程或者定解条件中加入描写新现象的数学项后会引起什么变化;等等。研究N-S方程的解析解在理论和实际应用上都具有重要意义。
叠加原理是线性微分方程理论的基础。对于非线性偏微分方程,由于不能运用叠加原理,目前还没有其求解的一般数学理论。求解N-S方程(8.13)的主要困难是:方程中对流项(v ·▽)v是非线性的。对于某些几何形状简单的流场,当流体沿某一坐标轴单向流动时,刚好使(v·▽)v恒等于零,这样就可以把N-S方程简化为线性方程,从而有可能求出解析解。这类解析解有:两平行平板之间的定常缝隙流动,沿斜平面的定常流动,完全发展的定常管流,同轴旋转圆柱面间的缝隙流动,沿有吸吮作用的平壁面的流动,非定常滑移运动平板所诱导的流动和圆管中非定常流动等。在另一类问题中,对流项(v·▽)v并不恒等于零,但却能够被化成较简单的形式,这样就使N-S方程简化为常微分方程,并且也能求出解析解。这类解析解有:收缩或者扩张通道中的平面定常流动,驻点附近的流动和旋转圆盘引起的流动等。作为例子,下面介绍三个第一类解析解的求解过程。
1.斜平面上液膜的定常流动
如图8-4所示,动力粘度为μ的液体在重力的作用下沿无穷大斜平面向下流动,斜平面与水平面之间的夹角为θ,液体膜的厚度为h,液面上为大气压,忽略液面与空气的摩擦。下面对此流动求解N-S方程。

图8-4 斜平面上液膜的定常流动
取坐标系如图。根据题意,y和z方向的速度分量v、w为零,压强沿x方向不变化,所有流动参数与z无关,同时也与时间变量t无关,单位质量力
![]()
根据这些特点,不可压缩流体的连续性方程(3.15)和粘性流体的运动微分方程(8.12)简化为

z方向的运动方程已经自动满足,因此没有列出。
这是一个定常流动问题,不需要给出初始条件。问题的边界条件是
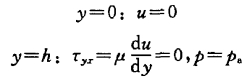
在y=0边界上,给定的是无滑移条件;在y=h边界上,给定的是切向应力和法向应力连续条件。
根据式(8.15a),可以把式(8.15b)进一步简化为


现在非线性的对流项已经消失,控制方程已经被简化为线性的常微分方程。对y积分,其中,(h-y)cosθ是液体中任意点相对于自由液面的淹深。可见,在液层中沿着y方向压强的分布与静止流体中的压强分布相同。
例8-2相距h的两块斜置平板,下板固定,上板以定常速度U在自身平面内向下滑移,两板之间充满动力粘度为μ的液体,液体在重力的作用和上板的拖动下运动,如图8-5所示。如果两板与水平面之间的夹角为θ,求流体的运动速度。
解 两板之间的流动与斜平面上液膜的定常流动具有同样的特点,因此可以对连续性方程和运动微分方程做同样的简化,从而得到控制方程(8.15)。对式(8.15)的前两式进一步简化,得


图8-5 两平行平板之间的定常流动
它与斜平面上液膜运动的微分方程相同,但是现在的边界条件为对微分方程积分两次,得
![]()
![]()

由边界条件解出积分常数
于是两板之间的流体运动速度
![]()
如果两板与水平面平行,夹角θ=0,则两板之间的流体运动速度
![]()

(8.14c)(z方向的方程)自然满足,运动方程(8.14)的前两式简化为

这也是定常流动问题,不需要提出初始条件。内、外柱面上的无滑移边界条件为
![]()
解常微分方程(8.18b),得其通解
![]()
由边界条件求出积分常数
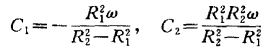
于是得到两个圆柱面之间的速度分布
![]()
如果外柱半径无穷大,即R2→ ∞,速度分布表达式(8.19)简化为
![]()
这就是第7章讨论过的平面点涡流动。此时可以把旋转的内柱看成是一个点涡(在三维空间中是一个线涡),它带动周围的流体做无旋运动。
把速度表达式(8.19)代入式(8.18a)后并对r积分就可以得到压强分布的表达式。不过,通常更关心的是圆柱与流体之间的摩擦力。
由柱坐标下的广义牛顿内摩擦定律(见附录)得到切应力
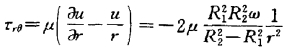
作用在内柱面上的流体摩擦力矩与内圆旋转方向相反。单位长度柱面上力矩的大小为
![]()
例8-3圆环形轴承中轴的半径R=40 mm,轴与轴承之间的间隙h=0.03 mm,轴长l=30 mm,轴转速n=3600 r/min,间隙中润滑油的动力粘度μ=0.12 Pa·s。求空载运转时的转矩。820这就是例4-17。在第4章中运用平面缝隙流的公式计算了转矩的近似值,现在用式(.)计算它的精确值。
解 根据题意,内圆柱半径R1=R=40 mm,外圆柱半径R2=R+h=40.03 mm,旋转角速度
![]()
把已知数据代入式(8.20)得到长度l=30 mm轴上的转矩
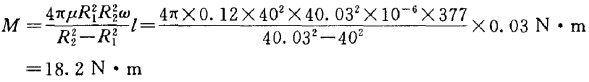
例4-17中的计算结果为M=18.1N·m。由于本例中轴与轴承之间的间隙相对于轴的半径确实很小,因此例4-17中的近似计算结果与这里得到的精确解相差不大。
3.无限大平板在自身平面内启动所带动的流体运动
无限大平板以上的半空间充满粘性不可压缩流体。设平板在t=0时刻突然启动,以定常速度U在自身平面内沿正x方向运动,并带动流体由静止开始流动,如图8-7所示。现在由连续性方程和N-S方程求解t>0时流体的运动。
这是一个非定常平面流动问题。根据问题的特点,有


图8-7 平板启动所带动的流体运动
质量力对流体运动的影响可以忽略,因此,连续性方程自动满足,运动方程(8.12a)简化为
![]()
式(8.12b)和(8.12c)自动满足。初始条件和边界条件为
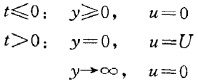
现在控制方程(8.21)仍然是一个偏微分方程,未知变量u是t和y的函数。为了把这个偏微分方程简化为常微分方程从而求出方程的解析解,首先运用量纲分析原理来减小问题所涉及的变量数。
采用无量纲速度u/U作为描述运动的一个基本参数,而u/U与ρ、μ、y、t等四个流动参数相关,它们之间的一般函数关系可以写为


表示综合参数。之所以在η表达式中乘以1/2是为了使后面将要得到的常微分方程更简洁;如果不乘以1/2,只会使常微方程中各项带有常数系数,但并不会影响求解过程。由于无量纲速度u/U只是η的函数,它的一般函数表达式又可写为
![]()
于是

其中,f′=df/dη,f″=d2f/dη2。运用这些关系式可以把运动方程(8.21)及初始、边界条件改写为

这样,通过引进无量纲变量就把偏微分方程转换成了常微分方程。
对常微分方程(8.22)求解,得到它的通解
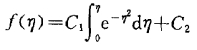
再利用常微分方程的两个边界条件解出积分常数

最后得到方程的解析解为
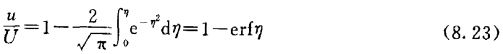

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















