相关系数计算

从图4-7可以看出，货运量与物流总产值之间呈现出一种直线趋势，也即呈现出正相关关系。但这只是定性地判断。要确切地判断它们之间的数量关系，即定量地进行判断，就要使用相关系数。相关系数是反映变量间线性相关关系密切程度和相关方向的一个统计指标。

相关系数计算方法有积差法和方差法两种，这里只介绍积差法。

积差法是利用各变量值与算术平均数的离差及离差平均数的大小来计算相关系数的。离差乘积和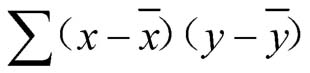的符号决定了两个变量的相关方向（正相关还是负相关），其数值大小与相关程度有关。的大小除与本样本容量多少有关外，还与x，y本身的数值大小有关，故还需要与各自的标准差对比，以消除这种不可比因素。故相关系数的积差法公式为：

其中：r——相关系数

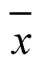——变量x的算术平均数

——变量y的算术平均数

σ_x——变量x的标准差

σ_y——变量y的标准差

式（4-32）又可写成：

【例4-13】

以表4-1中的数据为例，货运量与物流总产值相关系数的计算过程如表4-16所示。

表4-16 相关系数计算表

相关系数r的取值范围在 1～1之间，其性质可归纳如下：

（1）当｜r｜＝1时，表示变量x与y为完全线性相关，x与y之间存在着确定的函数关系。

（2）当r＝0时，表示y的变化与x无关，即x与y不相关。

（3）当0＝｜r｜＝1时，表示x与y存在着一定程度的线性相关。｜r｜的数值越大，越接近于1，表示x与y的线性相关程度越高。反之，｜r｜的数值越小，越接近于0，表示x与y的线性相关程度越低。

（4）当r＞0时，表示x与y为正相关。

（5）当r＜0时，表示x与y为负相关。

知识链接

简单线性相关分析的特点

（1）相关分析主要是计算相关系数，以反映变量之间关系的密切程度。

（2）分析时把两个变量的地位可以看成是对等的，不用分哪个是自变量，哪个是因变量，直接根据两个变量的数值即可计算相关系数。

（3）在存在互为因果关系的条件下，相关系数也只有一个。

（4）相关系数有正负号，表示相关的方向。

（5）计算相关系数时，所需的两个变量的资料都可以是随机的。