单样本检验

(一)正态性检验

例7-3　从某医学院男大学生中,随机抽取了22名男生,他们的身高如表7-1所示。假定全国成年男性的平均身高为172cm,问该医学院男生平均身高与全国成年男性平均身高是否不同钥

表7-1　某医学院22名男大学生身高　单位:cm

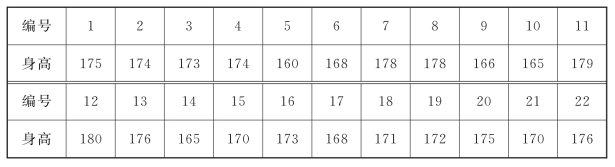
1.分析

一般可以认为身高、体重、血压等生理指标是属于正态分布的。为证实该样本来自于正态分布的总体,我们在进行t检验前须对该样本进行正态性检验。SPSS中正态性检验可通过“Explore”模块实现。数据录入的格式如图7-11所示。

2.操作

(1)“Analyze”→“Descriptive Statistics”→“Explore...”,出现的对话框如图7-12所示。

(2)在弹出的对话框左侧的变量列表中,单击选择本次检验的指标“身高”,点击最上面的“”按钮,将“身高”调入“Dependent List”栏中。

(3)点击“Plots...”,在弹出的对话框(见图7-13)中点击“Normality plots with tests”前的方框,使方框出现“√”,并点击“Continue”按钮。待返回如图7-12所示的界面后,单击“OK”按钮。

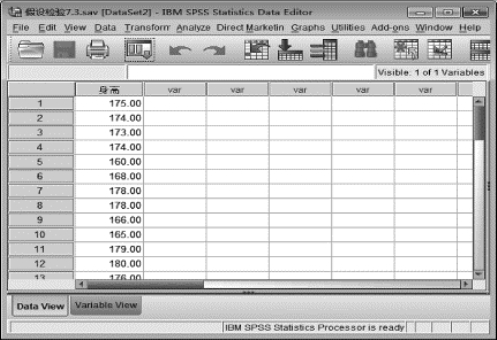
图7-11　例7-3的数据录入格式

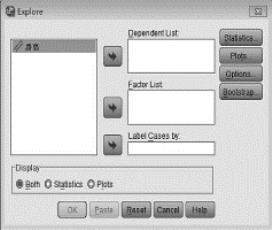
图7-12　例7-3正态性检验对话框

图7-13　例7-3正态性检验的Plots选项

3.界面说明

对如图7-12所示的界面简介如下:

(1)“Display”框:用于选择输出结果中是否包含统计描述、统计图或两者均包括。

(2)“Dependent List”框:用于选入需要分析的变量。

(3)“Factor List”框:如果想让所分析的变量按某种因素取值分组分析,则在这里选入分组变量。

(4)“Label Cases by”框:选择一个变量,它的取值将作为每条记录的标签。最典型的情况是使用记录号的变量。

(5)“Statistics...”:弹出Statistics对话框,用于选择所需要的描述统计量。有如下选项:

①“Descriptives”:输出均数、中位数、众数、5%修正均数、标准误、方差、标准差、最小值、最大值、全距、四分位全距、峰度系数、峰度系数的标准误、偏度系数、偏度系数的标准误及指定的均数可信区间。

②“M-estimators”:做中心趋势的粗略最大似然确定,输出四个不同权重的最大似然确定数。

③“Outliers”:输出五个最大值与五个最小值。

④“Percentiles”:输出第5%、10%、25%、50%、75%、90%、95%位数。

(6)“Plot...”:弹出Plot对话框,用于选择所需要的统计图。有如下选项:

①“Boxplots”:确定箱式图的绘制方式,可以是按组别分组绘制(Factor levels together),也可以不分组一起绘制(Depentends together),或者不绘制(None)。

②“Descriptive”:可以选择绘制茎叶图(Stem-and-leaf)和直方图(Histogram)。

③“Normality plots with test”:绘制正态分布图,并进行变量是否符合正态分布的检验。

④“Spread vs.Level with Levene Test”:当选择了分组变量时,绘制spread-versus-level图,设置绘图时变量的转换方式,并进行组间方差齐性检验。

(7)“Options...”:用于选择对缺失值的处理方式,可以是不分析有任一缺失值的记录、不分析计算某统计量时有缺失值的记录,或报告缺失值。

4.结果解释

例7-3进行正态性检验的主要结果如图7-14所示,SPSS 19.0软件对该组数据“身高”采用Kolmogorov-Smirnov和Shapiro-Wilk两种方法进行了正态性检验。每一种检验从左到右分别为检验统计量(Statistic)、自由度(df)、P值(Sig.)。结果显示P值分别为0.200和0.291,均大于0.05,因此可认为“身高”服从正态分布。

图7-14　例7-3正态性检验的结果

(二)单样本t检验

单样本t检验是常用于判断样本来自的未知总体均数与已知总体均数是否相等的方法。假设样本x 1,x 2,…,x n是简单随机样本,来自正态总体N(μ,σ2),方差σ2未知。在方差未知的情况下,对总体均值进行假设检验,检验统计量可采用自由度为n－1的t分布。检验统计量的计算公式为:

现对例7-3进行单样本t检验。

1.分析

“身高”为计量资料,且已对该数据进行了正态性检验,满足正态性。故可对例7-3采用单样本t检验。单样本t检验数据录入格式如图7-11所示。在SPSS中均值比较的模块为“Compare Means”。

2.操作

(1)“Analyze”→“Compare Means”→“One-Samples T Test...”,出现单样本t检验的对话框。

(2)在弹出的对话框左侧的变量列表中,单击选择本次检验的指标“身高”,单击“”按钮,将变量选入到“Test Variable(s)”框中。由于此次检验的目的是检验样本来自的总体均值是否为172cm,因此还须在“Test Value”右侧的空白框中填上“172”,如图7 15所示,并点击“OK”按钮。

(3)由于在统计学中置信水平通常为0.95,故SPSS软件中置信水平也默认为0.95。若置信水平为其他数值,可进行以下操作。单击“Options...”,在弹出的对话框“Confidence Interval Percentage”这一栏中,可输入可信区间的检验水准,如图7-16所示,点击“Continue”按钮(若检验水准为0.95可以不进行该步操作)。

图7-15　例7-3的t检验对话框

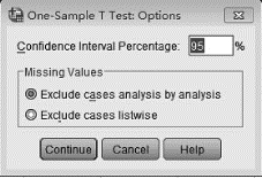
图7-16　例7-3的t检验的Options选项

3.界面说明

操作界面如图7-15所示,这里对界面中的部分按钮及选项介绍如下:

(1)“Test Variable(s)”:用于选入需要分析的变量。如果选入多个变量,可以分别进行多组的单样本t检验。

(2)“Test Value”:可输入已知的总体均数,默认值为0。

(3)“Options”:点击弹出Options对话框(见图7-16),用于定义相关的选项。

①“Confidence Interval Percentage”:用于输入需要计算的均数差值可信区间范围,默认为95%。如果是和总体均数为0相比,则此处计算的就是样本所在总体均数的可信区间。

②“Missing Values”:定义分析中对缺失值的处理方法,可以是具体分析用到的变量有缺失值才去除该记录(Exclude cases analysis by analysis),或只要相关变量有缺失值,则在所有分析中均将该记录去除(Exclude cases listwise)。默认为前者,以充分利用数据。

4.结果解释

例7 3进行t检验的主要结果如图7-17所示,计算出了平均身高与172cm差值的可信区间并进行了假设检验。其结果共分为以下5个部分。t值为0.082,自由度(df)为21,双侧检验的P值(Sig.(2-tailed))为0.935,样本平均身高与172cm的差值为0.09091cm,差值的95%可信区间为(－2.2065,2.3883)。由于双侧检验P＝0.935＞0.05,不拒绝零假设,因此还不能认为该班级男同学平均身高不等于172cm。

图7-17　例7-3单样本t检验的结果