教育成本函数

二、教育成本函数

教育成本函数是指在教育生产技术一定条件下教育产出与教育成本生产之间的关系。教育生产总成本函数可以用以下公式表示:

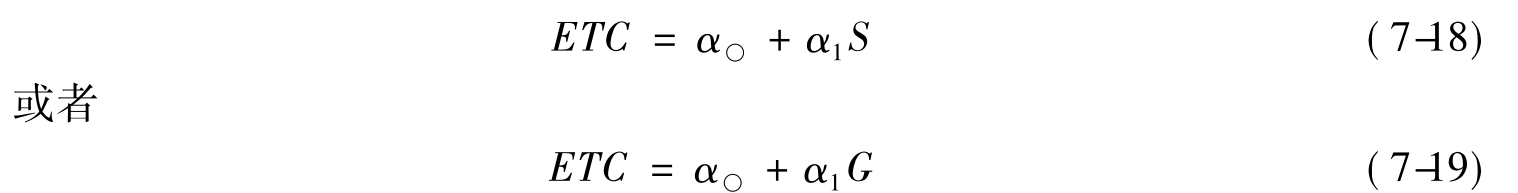
这里的α_○代表教育生产的固定成本(EPC)，α₁代表教育生产的边际成本(EMC)，S代表在校生数，G代表毕业生数，于是，α₁S就是按在校生数计算的教育生产的可变成本(EVC)，α₁G代表按毕业生数计算的教育生产的可变成本。公式7-18可以用图7-2来表示。

如图7-2所示，当在校生数为0时，教育生产总成本等于教育生产的固定成本，当在校生新增ΔS时，教育生产总成本新增ΔETC，于是，教育生产的边际成本就等于教育生产总成本新增量除以在校生新增量，即

那么，为什么EMC=α₁?对此我们证明如下:

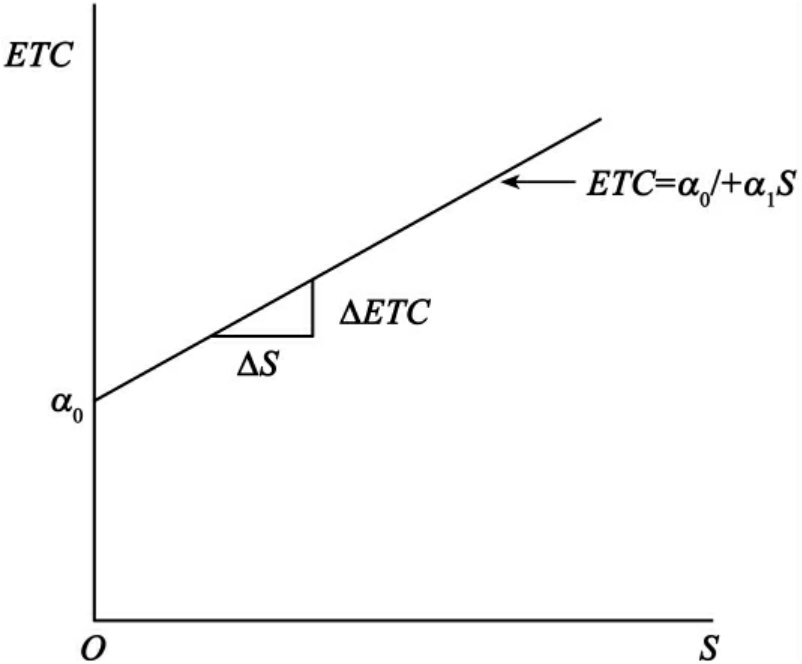
图7-2　教育总成本曲线

令S为50，于是有ETC₅₀=α_○+α₁50。令S为51，于是有ETC₅₁=α_○+α₁51。那么，新增的第51个学生的教育生产边际成本就是:EMC₅₁=ETC₅₁－ETC₅₀=(α_○+α₁51)－(α_○+α₁50)=α₁51－α₁50=α₁。证毕。

教育生产的平均成本的一种形式，即作为总成本分摊到每个在校生身上的在校生人均教育成本，由7-18可推导出如下表达式:

教育生产的平均成本的一种形式，即作为总成本分摊到每个毕业生身上的毕业生人均教育成本，也就有如下表达式:

从公式7-21或7-22来看，当在校生或毕业生无限增大时，α_○/S或α_○/G的值就无限缩小，于是，平均教育成本有接近于教育的边际成本的极小值，即EAC→α₁;当在校生或毕业生无限缩小时，α_○/S或α_○/G的值就无限增大，于是，平均教育成本有接近于教育总成本的极大值，即EAC→α_○+α₁。教育生产的边际成本与教育生产的平均成本的这种关系，可用图7-3来表示。

正如我们从表7-3中所看到的那样，只有当学班规模能无限扩大和无限缩小时，才有平均教育成本等于教育的边际成本的极小值和等于教育总成本的极大值，然而，学班规模是不能无限扩大和无限缩小的。在不考虑教育质量下降的情况下，平均教育成本有等于学班规模最大时的教育边际成本的极小值，有等于学班规模最小时的教育边际成本的极大值。然而，教育是不能不讲质量的。所以，平均教育成本的极值受制于适度学班规模。

现在我们把教育生产成本的讨论范围从一个学班扩大到一个学校。在坚持按适度规模学班办学的原则下，学校扩大招生规模最有效的方法是新增一个适度规模学班的人数，而只能从一年级开始招生。

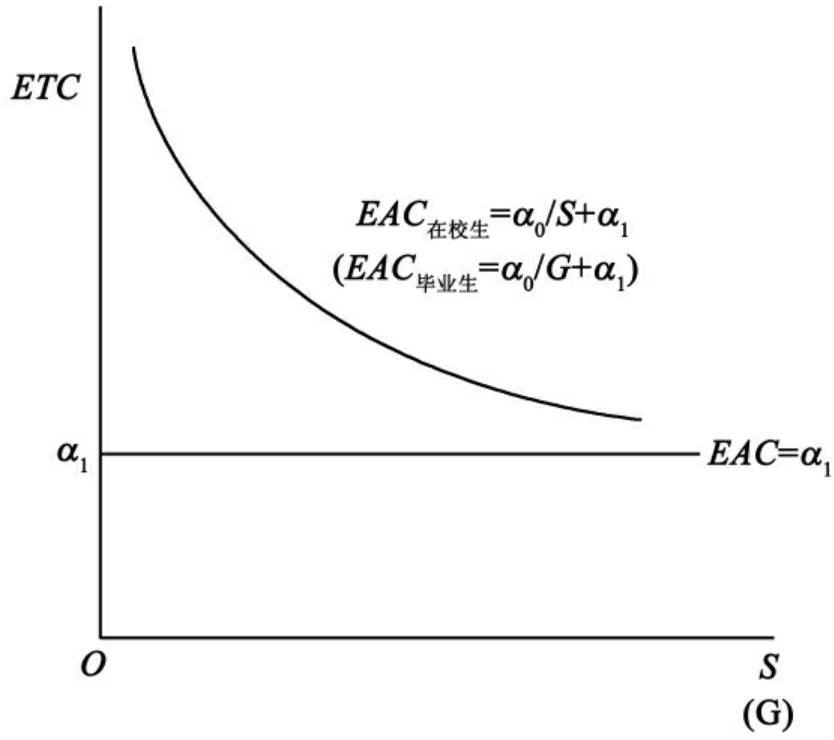
图7-3　教育总成本曲线

假定小学A是新建学校，适度规模学班为50人，从t₁年开始招收一年级新生，每年招收新生100人，正好满足两个适度规模学班的人数要求，那么，从t₁到t₆该校各年教育生产的总成本分别是:

ETC_t1=α_○+α₁100;

ETC_t2=α_○+α₂200;

ETC_t3=α_○+α₃300;

ETC_t4=α_○+α₄400;

ETC_t5=α_○+α₅500;

ETC_t6=α_○+α₆600。

在第t₇年以后的6年内，该校办学规模处于稳定。为了满足小学适龄人口不断增长的需求，该校决定一次性扩建12个教室，其他固定资产不变，从t₁₃年开始扩大招生，每年招收新生200人，正好满足四个适度规模学班的人数要求，那么，从t₁₃到t₁₈该校各年教育生产的总成本分别是:

ETC_t13=α_○+Δα_○+α₁₃700;

ETC_t14=α_○+Δα_○+α₁₄800;

ETC_t15=α_○+Δα_○+α₁₅900;

ETC_t16=α_○+Δα_○+α₁₆1000;

ETC_t17=α_○+Δα_○+α₁₇1100;

ETC_t18=α_○+Δα_○+α₁₈1200。

上述数据可以用图7-4来表示。

该校教育生产的平均成本从t₁年的α_○/100+α₁下降到t₆年的α_○/600+α₆，从第6年开始已有规模经济，教育生产的总成本曲线开始变得平缓。到第13年时，一次性扩建的12个教室不能全部投入使用，出现了规模不经济，教育生产的总成本曲线开始变得陡峭。随着教育生产的平均成本从t₁₃年的α_○/700+α₁₃下降到t₁₈年的α_○/1200+α₁₈，从第18年开始又有规模经济，教育生产的总成本曲线又开始变得平缓。

如果某个大学的教育生产总成本减去其固定成本正好是学生数与学院的教育生产总成本之积，而学院的总成本减去其固定成本又正好是学生数与系的教育生产总成本之积，即:

ETC_大学－α_○大学=ETC学院S ETC_学院－α_○学院=ETC系S

图7-4　小学A各年教育生产的总成本

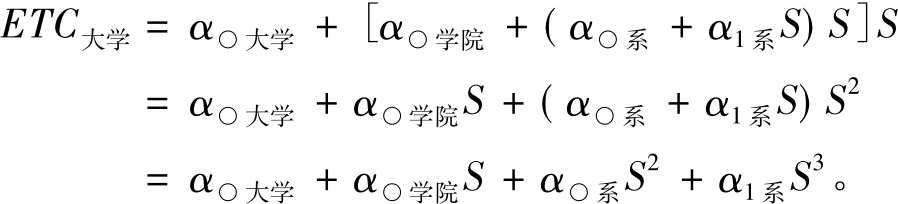
由于ETC系=α_○系+α_1系S，所以，该大学教育生产的总成本函数就是:令α_○学院=α₁，α_○系=α₂，α_1系=α₃，那么，我们就得到了该大学的教育生产总成本函数:

由公式7-23可推导出如下该大学的教育生产平均成本函数:

对公式7-23右边求导，便可得出如下该大学的教育生产边际成本函数:

令公式7-25中的自变量S=S₁，求y₁=f(S)=α₁+2α₂S₁+3α₃S₁²的导数，有:

如图7-5所示，在公式7-26中，当y₁'=α_○1时，S₁有最小值－α₂/3α₃。

令公式7-24中的自变量S=S₁，求y₂=f(S)=α_○/S₁+α₁+α₂S₁+α₃S₁²的导数，有:

这意味着，当边际成本曲线随在校生人数的增加而下降到最低点时，平均成本曲线还在随在校生人数的增加而下降，当边际成本曲线从最低点开始继续随在校生人数的增加而上升，并与继续下降的平均成本曲线相交时，其交点就是平均成本曲线的最低点。

图7-5　教育总成本曲线

如图7-6所示，教育生产的平均成本随学生人数的增加而下降，直到学生人数等于S₂。这时，该学校的规模经济潜力已用尽，这意味着S₂是该大学的最佳办学规模。如果该大学继续增加学生人数，就需增加固定资产，从而使教育生产的平均成本上升。

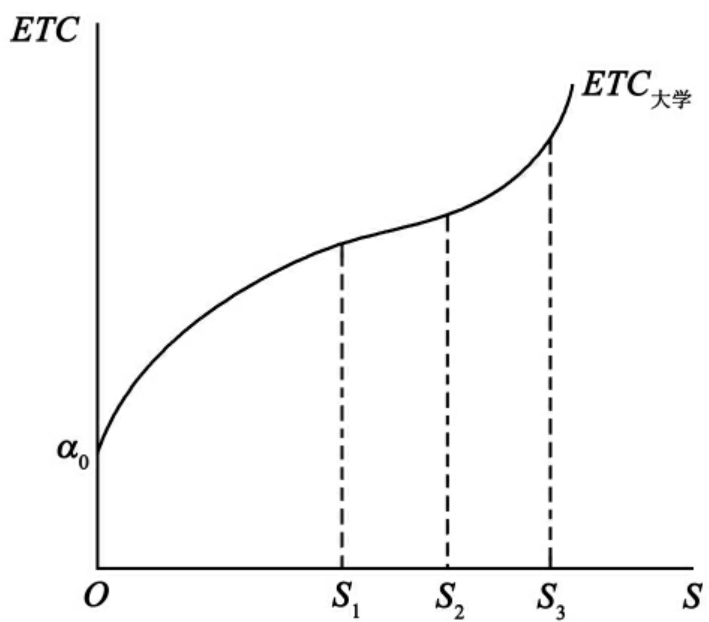
图7-6　教育总成本曲线

我们这里列举的是一个简化的例子，而在适度规模学班范围内，学校可能每班多招或少招几个学生，对教育质量的影响不会很大。