两种不同的分布模型及形成机理

11.3.1　两种不同的分布模型及形成机理

通过前两节的实证分析业已证明，布氏定律不仅适用于宏观层次的科学文献，而且适用于文献所含的微观层次的内容单元，还适应于网络信息。这说明，布氏定律客观地描述了情报、知识和信息离散分布的规律。

学术界对于布氏定律的认识和研究经历了一个逐步深化的过程。

最初，人们这样简单地解释文献分散的布氏定律：设想在某一新学科中写第一批论文时，人们首先把它寄给最合适的杂志发表。这些杂志伴随着该学科的发展，刊载越来越多的这类文章，于是许多著者都希望把他的文章发表在本专业的、以前发表了大量高质量论文的这类杂志上，使投稿数量大大增加，杂志对文章选择性增大，因而对文章的质量要求提高，杂志威信也日益提高，便产生了一些“核心”性的杂志。这种现象就是科学文献分布中的“堆加”效应。与此同时，有关这一学科的文章也在其他杂志上发表，这就产生了科学文献的集中与分散现象。

在以后的研究中发现，除了科学文献呈布氏分布外，社会科学的许多领域中也呈现出类似的分布。这些现象乍看起来毫无关系，但仔细观察就会发现它们并不是纯粹偶然因素的堆砌，不像许多自然现象那样受众多相互独立的、细微的、偶然的随机因素影响，而是受人的意志作用的一种有目的活动，具有十分明显的倾向性。人们写作时总爱选择常用的、传递功能强而消耗能量少的词汇；大城市总是人口集中的目标；杂志编辑部总希望选择质量较高的论文；科学工作者总是有目的地撰写论文，并把自己的论文寄给声誉较高、影响较大的杂志。对于这些受人的意志作用，倾向性很强的现象，只要我们用频次-等级排序法对其观测值进行处理，都会呈现出同样的分布，它所揭示的是这些观测值(具体元素)在其主体来源中的集中与分散规律。费尔桑提出了一个统一的表达式来描述这类分布⁽⁹⁾：

P(X)=C/X^P(1＜p≤2)　　　　　　　(11.1)

由人的控制因素支配的社会科学诸现象，包括情报现象，对观测值的概率密度分布常常服从上述分布式，我们称其为负幂分布。服从这种分布的现象，尽管其最初的表现形式不一定与式(11.1)完全相同，但总可以通过变换后得到与式(11.1)等价的表达式。

对于社会科学和情报学中的许多现象，这种呈现规律性的集中与分散是普遍存在的。于是有的研究者认为，在这方面存在着所谓“马太效应”，即“……谁若有，就给他，并不断增加；而谁没有，则连已有的都要被夺走。”有的研究者则认为，导致这种集中与分散规律的是“成功产生成功”的机理。这里“成功”有较广的含义，诸如：论文的写作与发表，收入增加，杂志声誉的提高，词汇被选用等。已取得的成功次数越多，就越容易在此基础上获得新的成功，例如高产作者撰写一篇论文十分容易，百万富翁增加一点收入毫无困难，声望高的杂志更容易获得高质量的稿件。这是个体自身能力和特性的显示。当一系列同类对象被选择时，这种个体性的差异就常常成为选择的依据，有的经常被选择，有的不常被选择。这种频度不均的选择又可以反过来作为再次选择的依据。如果我们把对象受到一次选择视为一次成功，那么，这种成功的累积必然导致新的成功。而频次-等级排序法正是将这些个性突出、经常被选择的元素排在高位，而把那些不常被选择的元素排在末位，从而表达了这类特殊的分布。⁽¹⁰⁾

与上面讨论的相反，某些现象受众多独立的、细微的因素影响，每一种因素都不起主导作用。例如在任意一段固定长的时间间隔内，由某块放射性物质放射出的α质点，到达某个计数器的质点数；从一个真空管的阴极发射出的电子到达阳极的电子数；来到某公共设施要求给予服务的顾客数(这里的公共设施诸如百货商店的售货员、工厂仓库的保管员、图书馆出纳员，机场的跑道、港口装卸货物的设备、电话交换台的干线等)；事故、错误、故障及其他灾害性事件数。

这些现象可以说是纯粹的随机现象，而且这些随机变量大致上都有如下特点：它们都取正整数为值，并且与时间间隔长度有关。当时间间隔极短，取值为2以上几乎是不可能的。例如，在极短的时间间隔内，可以认为不能有两个或两个以上的电话呼叫同时进入。另外，他们取值的概率与时间间隔的长度有关，而与从哪个时刻算起来没有什么关系，并且在不相重叠的时间间隔内，彼此没有什么影响。我们可以证明，在满足上述相应的条件下，这种与时间有关的随机现象服从泊松分布，我们可以称其为一个泊松过程或泊松流：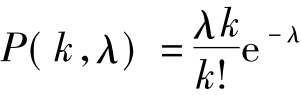

(k=0，1，2，…，λ为常数)　　　　　　　(11.2)

大量自然科学中的随机现象，或者只受偶然因素支配的一系列现象，都可以用泊松分布研究处理，与前面对应，我们称其为泊松分布系。

与泊松分布系相比，布-齐分布系无论从机理分析、适应范围还是数学表达都显得很不成熟。许多学者还从不同角度用量化方法模拟这种成功累积效应，导出了负幂型函数，即广义布氏分布模型。最有代表性的便是西蒙引入的球——罐子模型。这里，主体来源被看做了罐子，某一具体元素被看作投入罐子中的球。对布氏分布、齐夫分布、洛特卡分布、帕累托分布来说，罐子好比科学期刊、词汇集合、科学工作者居民集合等，球则好比相关文章、单词、所著论文、单位货币等。他设计有充分多的不同的罐子，在这些罐子中输入R个质量均匀的球。假定新进入罐子的球到达某一个罐子的概率与罐子内已有的球数成正比，求进入了r个球的罐子的个数n(rR)。结果得到与式(11.1)同型的负幂分布函数。经过变换，就可以得到布氏分布模型。

上述实验也可换一种方式进行。设想在一只袋中装着同样数量的红球和白球，每次从袋中随机取出一个球。如果是白球，视为失败，不再放回袋中。随着时间的推移，袋中的红球将会越来越多，白球则越来越少。求某一时刻从袋中取出红球的概率，结果与球罐子模型的结果一致。