第七节 正四棱台体积公式[7]——基于数学史的一则教学设计
对中西古代数学文化的深入研究,特别是这种历史的挖掘,目的还是为了指向现实、着眼于未来。本文给出的一则基于数学史的教学案例,正是笔者设想的在数学教育中通过数学史的渗透,在传统与现代之间架起一座桥梁,从而实现数学教育的现代化。
一、教学设计
(一)提出问题
师:我们已经学过了棱锥,我手上拿着的是一个正四棱锥的模型。如果我们在它顶部截去一个小的正四棱锥,就得到一个正四棱台(模型演示)。假如这个正四棱台下底面正方形边长为a,上底面边长为b,高为h,那么它的体积该如何表示呢?今天我们就来研究这个问题。
生1:既然正四棱台可以由一个大的正四棱锥截去一个小的正四棱锥得到,我就可以通过大正四棱锥体积减去小正四棱锥体积来求。(演算:设小正四棱锥高为x,则V=V大正四棱锥-V小正四棱锥=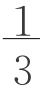 a2(h+x)-
a2(h+x)- b2 x=
b2 x=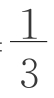 a2 h+
a2 h+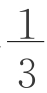 (a2-b2)x=…)我做不下去了。
(a2-b2)x=…)我做不下去了。
(二)类比、猜想、实验
师:这位同学的思路非常好,只是暂时遇到了困难。我们把这一问题放一边,先来猜想一下:
正四棱台体积的公式。大家回忆一下一些图形的面积和体积公式。(与学生一起填写下表)
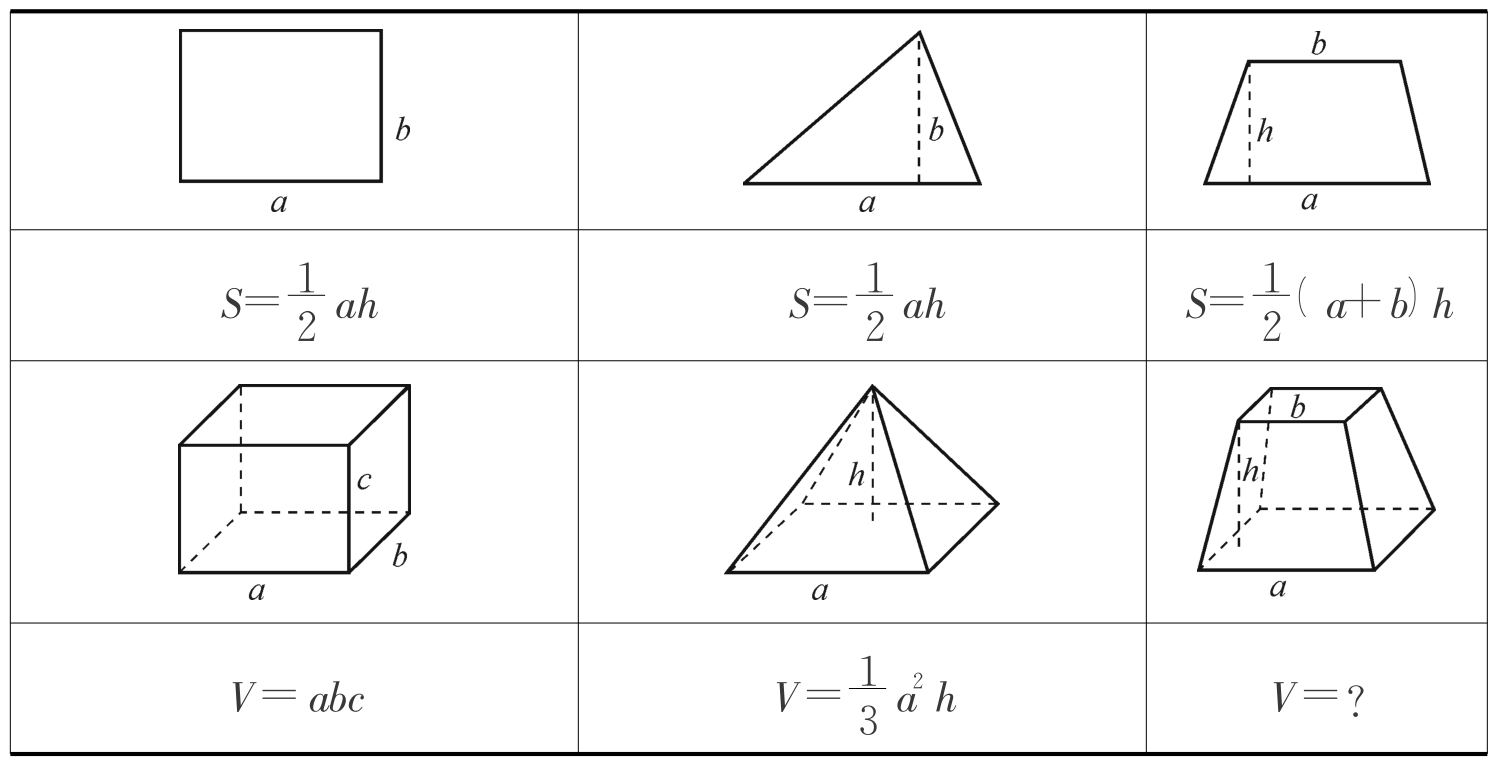
生2:我想V=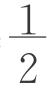 (a2+b2)h,因为梯形面积公式为S=
(a2+b2)h,因为梯形面积公式为S= (a+b)h。
(a+b)h。
生3:我觉得应该是V= (a2+b2)h,因为正四棱锥体积公式中有系数
(a2+b2)h,因为正四棱锥体积公式中有系数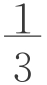 ,且当b=0时,V=
,且当b=0时,V=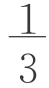 (a2+b2)h=
(a2+b2)h=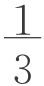 a2h,即为正四棱锥体积公式。
a2h,即为正四棱锥体积公式。
师:这些公式对不对呢?我们来做个实验。我这里有个空心的正四棱台容器,上底边长0.2m,下底边长0.3m,高0.2m,里面装满沙子。由生2的公式得沙子体积为V=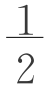 (0.04+0.09)0.2=0.013m3,由生3的公式得V=
(0.04+0.09)0.2=0.013m3,由生3的公式得V=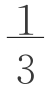 (0.04+0.09)0.2≈0.00867m3。我们再把沙子倒入底面边长为0.2m的柱形容器,量一下,高为多少?约为0.315m,体积约为0.0126m3。看来上面两个公式都不是很准确。
(0.04+0.09)0.2≈0.00867m3。我们再把沙子倒入底面边长为0.2m的柱形容器,量一下,高为多少?约为0.315m,体积约为0.0126m3。看来上面两个公式都不是很准确。
生4:梯形面积公式中系数是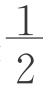 ,是因为括号内只有a、b两项。那么,如果正四棱台体积公式系数取
,是因为括号内只有a、b两项。那么,如果正四棱台体积公式系数取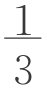 ,则括号内应有三项,除了a2、b2我想还应有ab,也即
,则括号内应有三项,除了a2、b2我想还应有ab,也即 h,计算
h,计算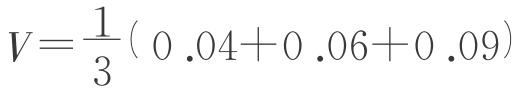 0.2≈0.0126。这与我们的实验结果一致。另外,当b=0时,V=
0.2≈0.0126。这与我们的实验结果一致。另外,当b=0时,V=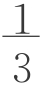 a2h是正四棱锥的体积公式;当h=b=a时,V=a3是正方体的体积公式。我想这个公式应该是正确的。
a2h是正四棱锥的体积公式;当h=b=a时,V=a3是正方体的体积公式。我想这个公式应该是正确的。
(三)推导公式
师:大家同意他的观点吗?(同意!)那好,下面我们就来证明或者说是推导这个公式。用什么方法来推导呢?刚才我们是通过类比的方法归纳出这个公式的,那我们能不能用类似求梯形面积的方法来求正四棱台的体积呢?我们不妨试试看,我先请同学们说出尽可能多的梯形面积公式的推导方法。
生5:(图2-7-1)S=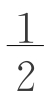 S平行四边形=
S平行四边形=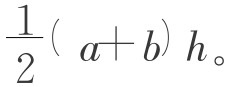
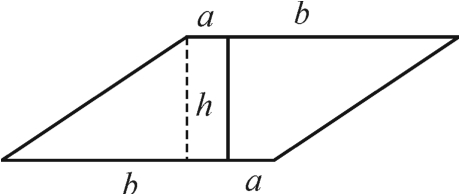
图2-7-1
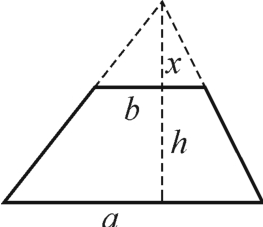
图2-7-2
生6:(图2-7-2)设小三角形高为x,大三角形高为x+h,因为这两个三角形相似,所以 ,即x=
,即x=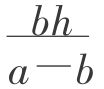 。S=
。S=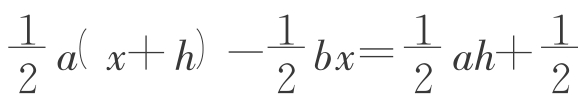 (a-b)x=
(a-b)x=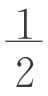 ah+
ah+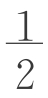 (a-b)
(a-b)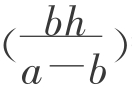 =
=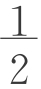 (a+b)h。
(a+b)h。
生7:(图2-7-3)S=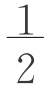 ah+
ah+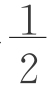 bh=
bh=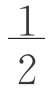 (a+b)h。
(a+b)h。

图2-7-3
生8:(图2-7-4)S= (a-b)h+bh=
(a-b)h+bh=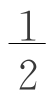 (a+b)h。
(a+b)h。
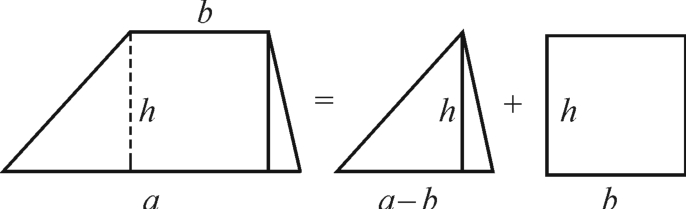
图2-7-4
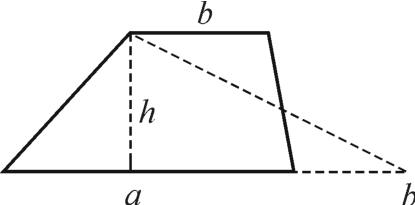
图2-7-5
师:有没有其他方法?还记得我们以前是如何证明梯形中位线定理的?
生9:(图2-7-5)S=S三角形=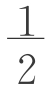 (a+b)h。
(a+b)h。
师:接下来我们就利用类似的方法试着来推导正四棱台的体积公式。第一组用生5的方法,第二、三、四组同学分别用生6、生7、生8的方法。如果你觉得这种方法做不出或者做出来了,请再用生9的方法推导。(学生独立思考、互相讨论来解决问题,教师适当介入,给予提示指导。当第四小组完成其推导后,教师再给他们一道思考题:有这样一个四棱台,它的两个底面是长方形。上底面边长分别为a、b,下底面边长分别为c、d,高h,求其体积。)
(四)展示成果
第一组(生10):我们认为利用两个或多个正四棱台拼在一起无法推导其体积公式。
第二组(生1):刚才我做不下去,现在我会了。(继续= a2h+
a2h+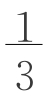 (a2-b2)
(a2-b2) a2h+
a2h+ (a+b)bh=
(a+b)bh=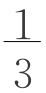 (a2+ab+b2)h)
(a2+ab+b2)h)
第三组(生11):我们将正四棱台分成五个棱锥A、B、C、D、E。(图2-7-6)
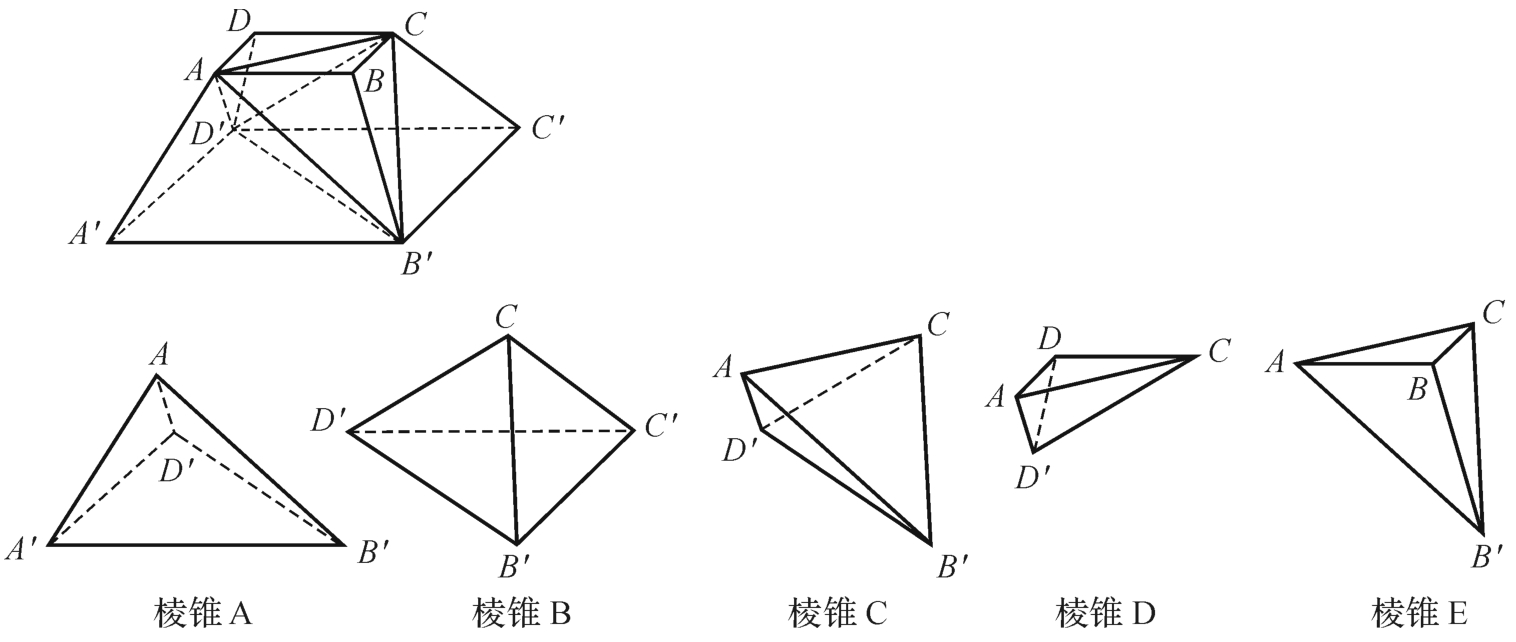
图2-7-6
其中VA+VB=2VA=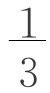 a2h,VD+VE=2VD=
a2h,VD+VE=2VD=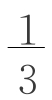 b2h。对于锥体C(图2-7-7),我们取AC中点O,连接B′O、D′O,容易看出AC⊥面B′OD′。取B′D′中点O′,连接OO′,则OO′⊥B′D′。所以,VC=
b2h。对于锥体C(图2-7-7),我们取AC中点O,连接B′O、D′O,容易看出AC⊥面B′OD′。取B′D′中点O′,连接OO′,则OO′⊥B′D′。所以,VC=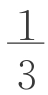 S三角形B′OD′AC=
S三角形B′OD′AC=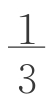 ・
・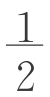 ・B′D′・h・AC=
・B′D′・h・AC= abh。由此得V=VA+VB+VC+VD+VE=
abh。由此得V=VA+VB+VC+VD+VE=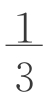 (a2+ab+b2)h。
(a2+ab+b2)h。
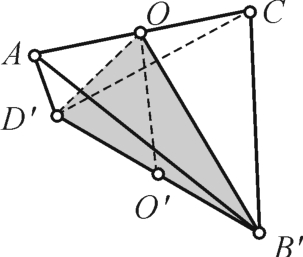
图2-7-7
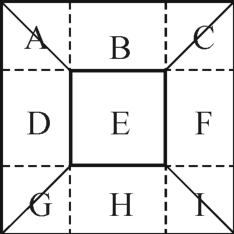
图2-7-8
第四小组(生12):我们将正四棱台切割成九部分(图2-7-8):(1)一个长方体E,其底面是边长为b的正方形,高为h,体积为b2h。(2)四个棱锥A、C、G、I,可以拼成一个大的四棱锥J,起底面是边长为(a-b)的正方形,高为h,体积为 (a-b)2h。(3)四个直角三棱柱B、D、F、H,可以拼成两个长、宽、高分别为b、
(a-b)2h。(3)四个直角三棱柱B、D、F、H,可以拼成两个长、宽、高分别为b、 、h的长方体K和L,体积均为
、h的长方体K和L,体积均为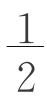 b(a-b)h。所以,(图2-7-9)V=VE+VJ+VK+VL=b2h+
b(a-b)h。所以,(图2-7-9)V=VE+VJ+VK+VL=b2h+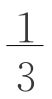 (a-b)2h+b(a-b)h,整理得V=
(a-b)2h+b(a-b)h,整理得V=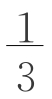 (a2+ab+b2)h。
(a2+ab+b2)h。
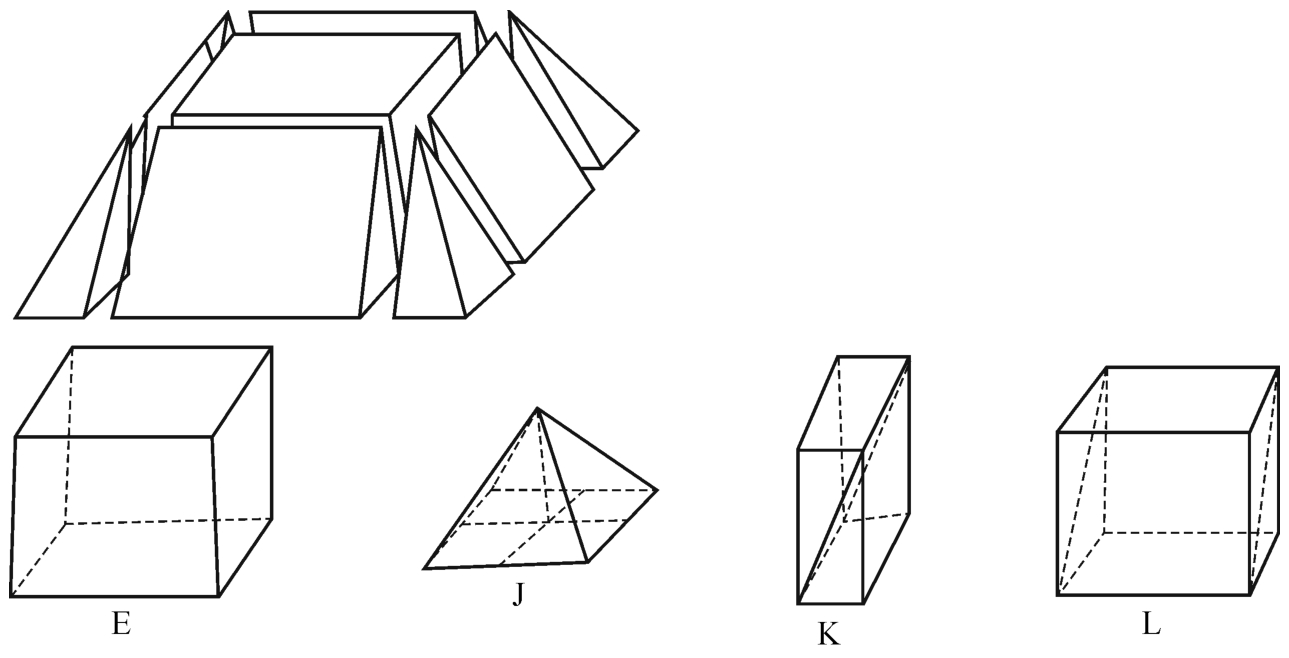
图2-7-9
生13:同样方法可以求出思考题中四棱台体积:

当a=b、d=c时,V= (2a2+ac+2c2+ac)=
(2a2+ac+2c2+ac)=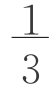 (a2+ac+c2)h。
(a2+ac+c2)h。
生14:利用类似生9的方法来推导比较繁杂,我用图示的方法来说明。为了使大家看得清楚,我把它先分成四等分,且选择其中一块(图2-7-10)。把这一块分成三部分,这三部分又可以拼成一个不规则图形,这个图形的体积可以通过补形法求得。

图2-7-10

(五)教师总结
上面几位同学向大家展示了他们的研究成果,非常出色。同学们可能不知道,这个公式在距今4000年前就已经被古埃及人所掌握。成书时期约在公元前1850年的一册古埃及数学课本中就记载了一道计算正四棱台体积的问题。数学史家贝尔称这个问题为“最伟大的埃及金字塔”,在他看来,这个问题中涉及的归纳算法较之今日仍旧巍然耸立的任何一座由巨石堆砌而成的古埃及金字塔要雄伟得多。
那么古埃及人是如何得到这一公式的呢?我们现在已经无法知道这个公式的确切来源了。第三组同学展示的推导方法简洁优美,并且公式与图形联系紧密,我们可以猜测古埃及人可能是通过这种方法得到的。
在我国古代,《九章算术》给出了刍童(即两底是长方形的正四棱台)的体积公式V=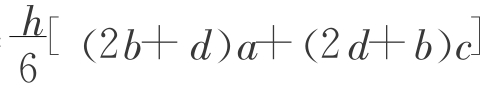 。同学们一定注意到了生13给出的思考题的解法。我国古人就是利用这种分割方法得到刍童体积公式的。
。同学们一定注意到了生13给出的思考题的解法。我国古人就是利用这种分割方法得到刍童体积公式的。
古代巴比伦人曾使用过错误公式V=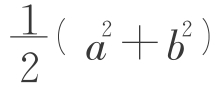 h——注意这个错误我们也犯了,——后来的古巴比伦泥板文书上也记载了相当于下式的计算法则V=
h——注意这个错误我们也犯了,——后来的古巴比伦泥板文书上也记载了相当于下式的计算法则V=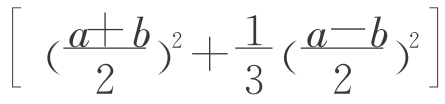 h。大家也一定注意到了,生14的推导中也出现了这种形式。为什么古巴比伦人没有把它写成古埃及人的形式呢?虽然它可以转化成那种形式。也许,古巴比伦人用的是不同于古埃及人的方法,可能利用的就是生14的方法。
h。大家也一定注意到了,生14的推导中也出现了这种形式。为什么古巴比伦人没有把它写成古埃及人的形式呢?虽然它可以转化成那种形式。也许,古巴比伦人用的是不同于古埃及人的方法,可能利用的就是生14的方法。
生15:老师,我打断一下,你说V=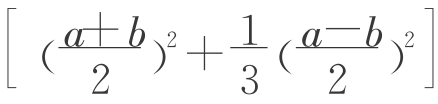 h是古巴比伦人的公式,并且可能是利用生14的方法。我刚才在用类似生12的方法对棱台作进一步分割,推导过程中也出现这个形式。当时我觉得这样很繁没有提出来,现在我想给大家演示一下,也许古巴比伦人是利用我这种方法推导的。我也像生14选用其中1/4块来用图说明(图2-7-11)。把这一块切割成13块,再拼成一个长方体,还剩两个小锥体。
h是古巴比伦人的公式,并且可能是利用生14的方法。我刚才在用类似生12的方法对棱台作进一步分割,推导过程中也出现这个形式。当时我觉得这样很繁没有提出来,现在我想给大家演示一下,也许古巴比伦人是利用我这种方法推导的。我也像生14选用其中1/4块来用图说明(图2-7-11)。把这一块切割成13块,再拼成一个长方体,还剩两个小锥体。
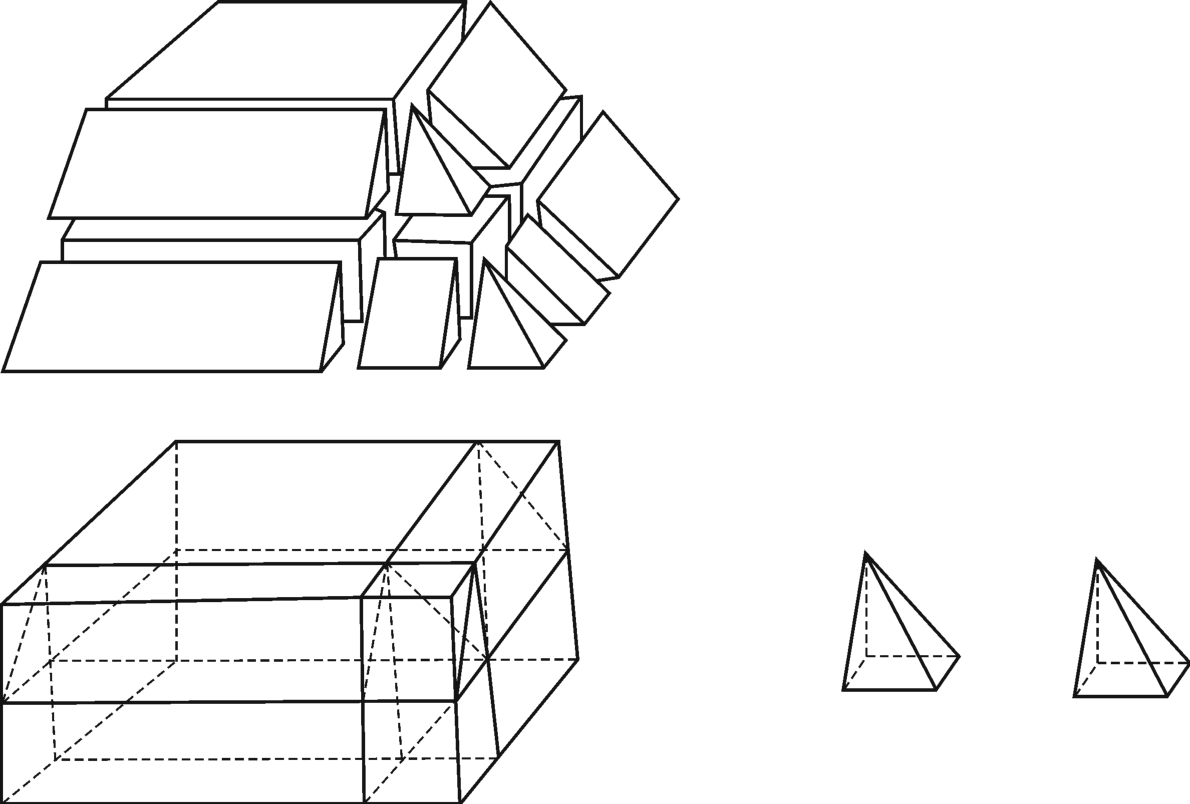
图2-7-11
![]()
二、案例点评
新教材(人民教育出版社《数学》(实验修订本))已经取消了台体及其体积公式这一内容。但是这块内容背后所蕴涵的思维价值远远大于这个公式本身的实用价值。所以,可以把它用来作为课外活动、兴趣小组以及研究性学习的课题,让学生在探索的过程中体验数学、欣赏数学。我们也可以预见若干年以后高考中会出现这样一道题目:先阅读一段关于正四棱台的定义、正四棱锥的体积公式以及推导梯形面积公式的几种方法的材料,再让学生写出正四棱台的体积公式以及推导这一公式的几种方法。2002年全国高考卷文科最后一题就传递了这样一种信息:关注平面图形与空间图形的转化和类比。
关于台体体积的教学,如果单是为了让学生记住公式,并利用公式计算,确实不难。只要将公式及某种推导方法直接告诉学生,然后证明,再通过大量练习进行巩固。这样也能达到一定的教学效果。可是,如果真是这样机械处理的话,那就大大忽略了让学生发现结果和探索问题的思维过程,失去了训练思维的绝好机会。上述案例的可贵之处在于通过对数学史材料的深入挖掘以及对学生认知水平的合理定位,把火热的思维过程展现在了课堂中。在这个过程中,可以说学生重演了人类对这一公式的认识历程,经历数学真理发现与发展的过程,体验经过艰辛摸索后成功的愉悦,这对他们今后学习数学、学好数学都是十分有益的。
以往教学只介绍一种推导方法(如第二组展示的),这样思考问题显得思路狭隘,限制了学生从多角度思考。这则案例的处理则走向开放化,让学生从多角度思考问题,用多种方法来解决问题。通过观察、类比、实验、猜想,培养了学生的数学思维能力,同时也调动了学生学习数学的积极性。
这个案例还有个突出的特点,那就是引入了数学实验。传统的数学教学常以严密的逻辑推理来论证因而排斥实验,因而数学课堂中基本上看不到实验的影子。然而,许多数学发现实际上都源于实验,同时实验也可以用来检验猜想。在数学教学中适当引入实验,对学生体验思维过程及数学思想都十分有利。在这里,通过猜想—实验—再猜想—再实验—得出正确的猜想—证明,学生完成一个完整的知识建构过程。
更进一步,这则教学案例不仅介绍了公式的最早记载,同时在教学过程中还隐含了对不同文化背景下的数学的比较。虽然没有事先说明,但学生重演了古埃及人、中国古人以及古巴比伦人对这一问题的处理过程。通过对这些方法的探索和比较,学生能欣赏到数学的美以及整个人类的智慧。多元文化背景下的数学教育让学生欣赏各种数学,而不管它是否属于自己的传统文化。包含各种文化根源的数学可以让学生形成丰富的体验,明白其他文化对数学发展所做的伟大贡献。这种教育的意义已经超出了数学课程的目标,但这确实是数学可以给予的。
参考文献
[1]张维忠.数学文化与数学课程[M].上海:上海教育出版社,1999.
[2][美]莫里斯・克莱因.古今数学思想[M].上海:上海科学技术出版社,2002.
[3]David Nelson,George Gbevergbese Joseph,and Julian williams.Multicultural Mathematics[M].Oxford University Press,1993.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















