第十二节 数列的递推公式[12]——一则基于数学文化的探究教学课实录
浙江师范大学与浙江省丽水市的两所中学合作开展一年的校本教研培训活动,培训形式除了专家讲学外,大量的是“同课异构”式的教研活动。2008年3月14—15日在浙江丽水中学、丽水学院附中就高一年级的高中新课程必修5第2章“数列的递推公式”(数列复习课第1课)进行了4节公开课教学。同一内容分别由浙江丽水中学、温州中学与丽水学院附中的教师执教,其中温州中学执教的李芳老师的教学设计是在温州中学特级教师马玉斌老师以及浙江师范大学张维忠教授等专案指导下完成的,而且她又是唯一有机会就同一内容讲授2次的执教老师。下面给出的是李芳老师前后两次上课的教学实录与我们的思考。
一、初次上课实录
(一)回顾
回顾一:复习等差数列、等比数列的定义式(递推公式)及通项公式,为后面由递推公式推导通项公式做铺垫。
回顾二:必修5中2.1的例2:谢宾斯基三角形。
1.介绍数学的历史与文化
上世纪初,波兰的数学家谢宾斯基想要找到一个图形,当它的面积无限减小时,它的周长则无限增大。(用几何画板进行迭代演示)
2.数一数
将上述迭代过程逐一展示,让学生数数在每个图形中绿色(图3-12-1,图中绿色为浅色,黑色为深色,图3-12-2、图3-12-3同)三角形的个数依次为多少?引出该等比数列的递推式及通项公式。
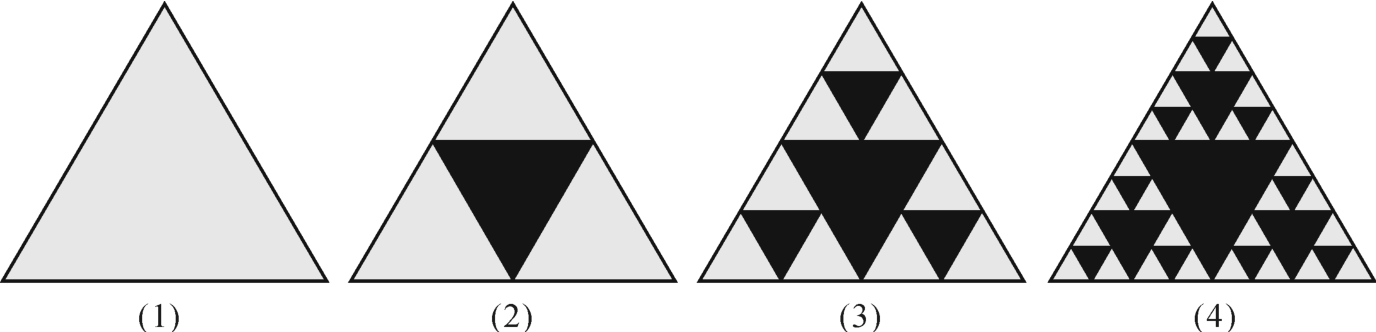
图3-12-1
(二)探究
1.再数一数
每个图形中绿色、黑色三角形的总个数依次为多少?
学生容易先得出前三项为1,4,13。
探究一:第4项是多少?(从特殊到一般,引出递推公式)
方法一(几何方法)
从第(2)个图起,每一个图形可以看成由前一个图形的三份缩影加上中间一个黑三角形。因此,bn=3bn-1+1(n≥2)。
方法二(代数方法)
从前三个图的数值上也可以发现:bn=3bn-1+1(n≥2),
所以b4=3b3+1=3×13+1=40。
方法三(代数方法)
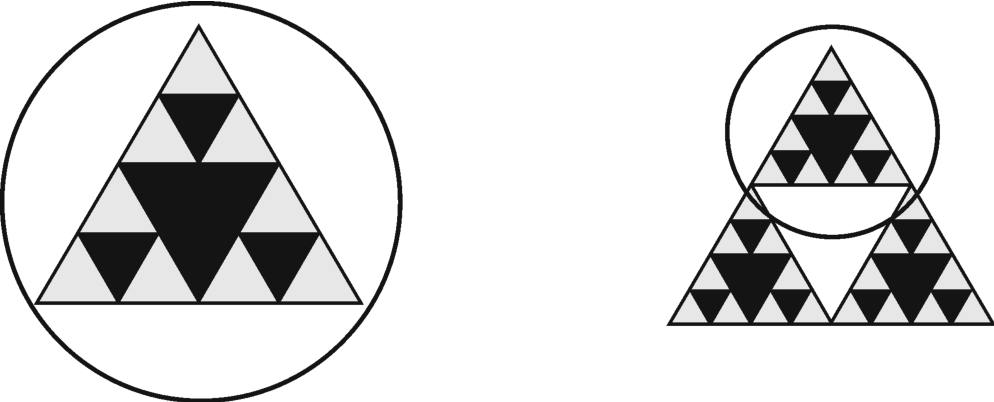
图3-12-2
因为b2-b1=3,b3-b2=9,b4-b3=27,所以猜想bn-bn-1=3n-1(n≥2)。
所以b4=b3+33=13+27=40。
方法四(几何方法)
从第(2)个图起,每一个图形是在前一个图形的每个绿三角形中挖走一个中心三角形,这样如图3-12-2所示的圈内一个三角形就变为四个三角形,增加三个三角形。
在第n-1个图形中,绿三角形的个数为3n-2,所以bn=bn-1+3n-2×3,即bn=bn-1+3n-1(n≥2)。
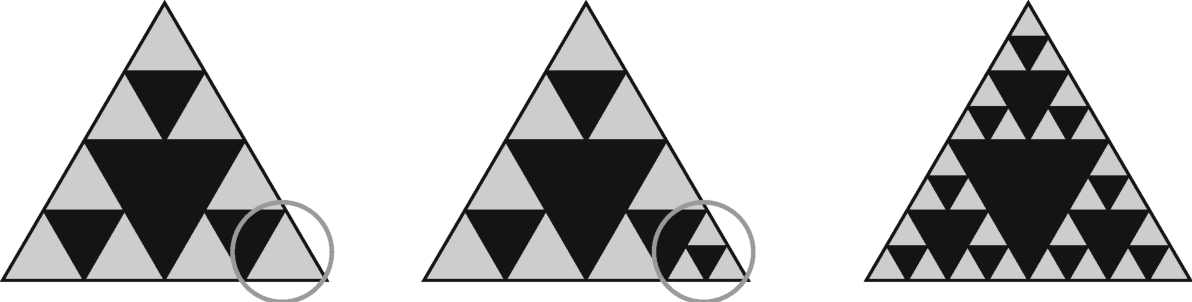
图3-12-3
归纳:当我们面对较为一个复杂的数列时,很难一眼看清其全貌的话,可以先寻找出其递推关系,这就是本堂课复习的重点——数列的递推公式。
递进:然而,我们得到该数列的递推公式便满足了吗?请问,它的方法一的引导:
教师让学生观察递推公式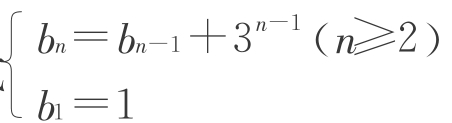 ,提问:由
,提问:由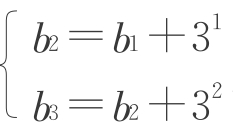 如何得b3?从而,诱导出利用“累加法”来解决此问题。
如何得b3?从而,诱导出利用“累加法”来解决此问题。
由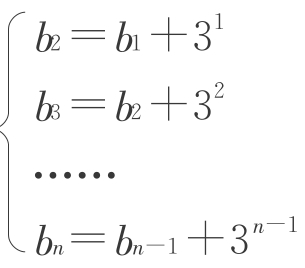 累加得:bn=b1+31+32+…+3n-1=
累加得:bn=b1+31+32+…+3n-1=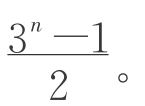 第5项是几?第6项是几?(学生轻松回答)那么,第100项是几呢(学生一时语塞,随即提笔思考)?
第5项是几?第6项是几?(学生轻松回答)那么,第100项是几呢(学生一时语塞,随即提笔思考)?
探究二:第100项是多少?(引出求通项公式的方法)
教师小结以上解法:
其一,用了累加法,此法早在等差数列中由定义式推导通项公式就曾用过,类似的还有累乘法。
其二,用了等比数列求和公式。
方法二的引导:
教师再让学生观察递推公式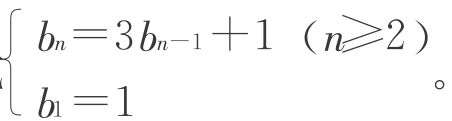 在递推式bn=3bn-1+1(n≥2)中,若去1,就是等比数列;若改3为1,则是等差数列。是否可构造以3为公比的等比数列呢?如何把常数1进行分配呢?假设等式左边分得m,则右边就得3m。所以有:
在递推式bn=3bn-1+1(n≥2)中,若去1,就是等比数列;若改3为1,则是等差数列。是否可构造以3为公比的等比数列呢?如何把常数1进行分配呢?假设等式左边分得m,则右边就得3m。所以有:
令bn+m=3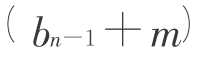 ,则m=
,则m=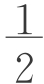 。即
。即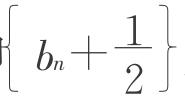 为以b1+
为以b1+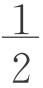 为首项,3为公比的等比数列。
为首项,3为公比的等比数列。
所以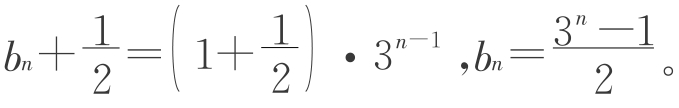
小结:这可谓“殊途同归”!同一个数列有两个不同的递推公式,两个不同的递推公式推出同一个通项公式,虽分别用了“累加法”和“构造法”,但却都是化归为等差或等比数列的有关概念来解决!
探究三:试由递推公式推得数列的通项公式
给学生一些思考时间。部分学生均只能由已知条件求出第3项为9,第4项为13,则猜想就是前面的数列{bn}。教师则引导从bn=3bn-1+1(n≥2)开始出发,是否可再构造等比数列?即
令bn+1+mbn=t(bn+mbn-1),则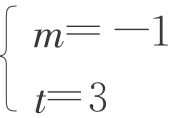 ,或
,或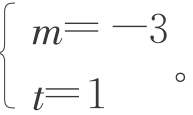
即为探究二中的两个递推公式,当然此数列就是前面的数列{bn}。
(三)巩固思考
已知数列{an}满足a1=1,an+1+an+1an=an,试写出该数列的前三项,并归纳它的通项公式。
意图:①让学生再次经历特殊到一般的归纳过程,培养合情推理的能力;②从归纳的结果中发现通项的分母为等差数列的通式,从而为严格论证开启思路。
(四)归纳小结
当我们研究一个较为复杂的数列时,若不能马上得出它的通项公式,可以先通过其特殊项或其蕴含的几何背景来发现它的递推公式,然后利用累加法、累乘法和构造法等,将递推公式化归为等差数列、等比数列的有关问题,从而最终求出数列的通项公式!

图3-12-4
(五)课外作业
(1)若数列{an}满足a1=1,an+1=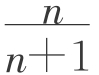 an,则an=_________。
an,则an=_________。
(2)在三角形纸片内有n个点,连同三角形的顶点共(n+3)个点,以这(n+3)个点作为小三角形的顶点,设三角形纸片最多可以剪成an个小三角形.如a1=3,a2=5.试写出数列{an}的通项公式。
(3)试说明谢宾斯基三角形的面积与周长的变化特征。
二、改进后上课实录
以上是第一天在丽水中学上课的课堂实录,课堂上学生探究的效果不理想,前段与后段较好,中间探究部分还不能很好地引起大多数学生的共鸣。在当天的评课专题研讨会上专家与丽水中学的数学老师给出了许多建设性的改进意见,李芳老师将案例做了如下的修改,第二天在丽水学院附中授课,教学效果甚好。以下是第二天在丽水学院附中上课的课堂实录(为了便于前后对照,下面标题的序号与前面初次上课的教学设计标题序号相同,内容相同部分将略去)。
(一)回顾
改进:知识直接性复习引入改为问题背景式引入。
如:写出下列数列的通项公式?
(1)1,3,5,7,…
(2)1,4,16,64,…
生:(1)an=2n-1;(2)bn=4n-1。
师:你是怎么求出来的?(等差、等比数列的通项公式)为什么数列(1)是等差数列(2)等比数列?(因为:an+1-an=2,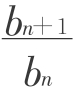 =4)这样就复习了前面的知识,为后面的探究作好铺垫。
=4)这样就复习了前面的知识,为后面的探究作好铺垫。
(二)探究
探究二改进:提出问题,即数列的第100项是多少?(引出求通项公式的方法)
一开始,教师先不引导,而是给学生一定的思考时间。
(教师的行为改变了,学生的反映也随即发生了变化……)
不久,学生甲在其草稿纸上写下:
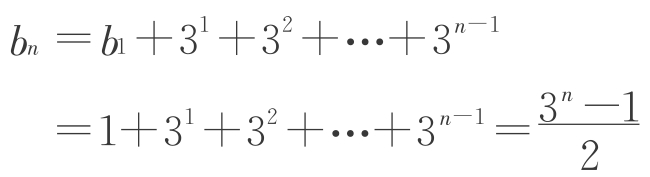
教师小结以上解法:
其一、其二同初次上课的教学设计。
其三,从学生探究的结果bn=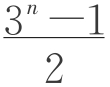 出发,其表达式子中是否存在等比数列?等比数列的本质是什么?3n,
出发,其表达式子中是否存在等比数列?等比数列的本质是什么?3n,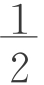 ・3n等形式,再启发学生化归为:2bn+1=3n,bn+
・3n等形式,再启发学生化归为:2bn+1=3n,bn+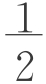 =
=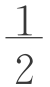 ・3n,2bn+1-2bn=3,bn+1-bn=
・3n,2bn+1-2bn=3,bn+1-bn=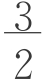 等形式,进而发现数列
等形式,进而发现数列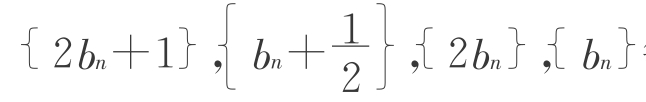 等均应为等比数列(为另一递推公式构造等比数列推导通项公式创造条件)。
等均应为等比数列(为另一递推公式构造等比数列推导通项公式创造条件)。
探究三改进:寻找递推公式中的几何背景
先给学生充分的思考时间。
生甲:我求得了b3=9,b4=13,所以我猜测就是前面的数列,即bn=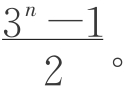 当然这有一定的局限性。
当然这有一定的局限性。
生乙:我根据式子的特征,将一个bn移到等号左边,得:bn+1-bn=3(bn-bn-1),则{bn+1-bn}为以3为公比的等比数列……
教师小结:
其一,对于乙同学的解法,教师先给予充分肯定,再提出思考,你怎么看出从等号右侧移一个bn到左侧呢?一般情况下,如何解决呢?引出利用待定系数法构造等比数列的方法。(见初次上课的教学设计)
其二,前面的递推式我们均能从几何背景找到它们的解释,对于此递推公式,仍能从谢宾斯基三角形中得到验证吗?
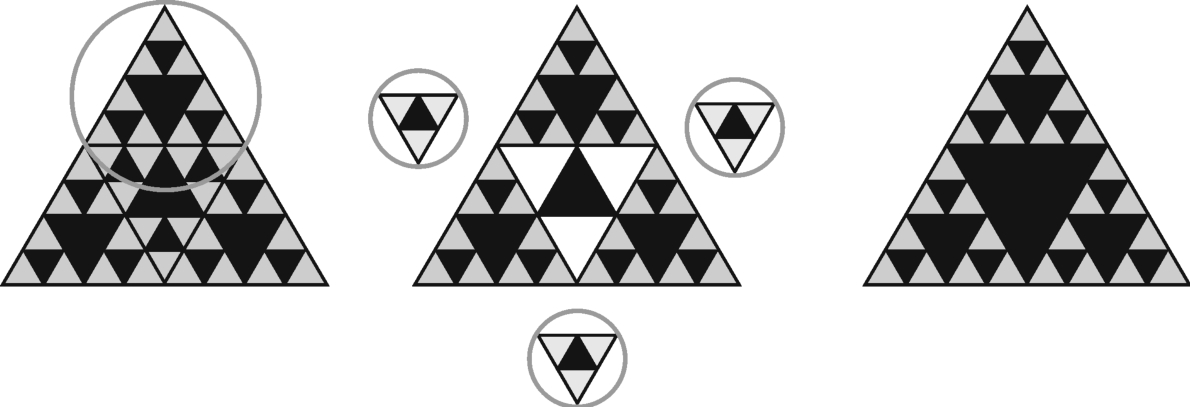
图3-12-5
四个图案(3)的缩影除去三个图案(2)的缩影即可得图案(4),即有bn+1=4bn-3bn-1(n≥2)。同时,辅以几何画板的动画演示,结果更加形象,引起学生极大的兴趣!
三、点评
《普通高中数学课程标准(实验)》指出:“数学是人类文化的重要组成部分。数学课程应适当反映数学的历史、应用和发展趋势,数学对推动社会发展的作用,数学的社会需求,社会发展对数学发展的推动作用,数学科学的思想体系,数学的美学价值,数学家的科学精神。”而“数列的递推公式”是高中新、旧教材均有的代数内容,看起来比较简单。即:了解递推公式是给出数列的一种方法并能根据递推公式写出数列的前几项。但执教者给出的教学设计却是“源于教材,高于教材。”谢尔宾斯基三角形原本是新教材中的一个例题,只给出了数列前面几项。执教者的教学设计结合张维忠著的《文化视野中的数学与数学教育》第10章内容作了深度挖掘。从谢尔宾斯基三角形出发,引导学生探究数列的递推公式,由于有先前一节课的经验,第二次改进后的教学设计留给学生的探究梯度恰当,加上数学历史与文化的渗透,学生的参与度很高,真正实现了师生互动。数形结合的思想以及数学的本质:模式建构都得到了充分体现。
进一步,通过使用数学教学软件“几何画板”现场制作谢尔宾斯基三角形,并演示其中的变化,寻找递推公式an+1-an=2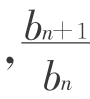 =4,bn=bn-1+3n-1(n≥2),bn+1=4bn-3bn-1(n≥2)等的几何背景,学生从谢尔宾斯基三角形的一系列变化中观察出了数列中项数的变化及其各种关系。具体讲,从探究图中绿色三角形个数的计数问题自然过渡到对图中绿色、黑色三角形总个数的计数问题探究。这种从不同视角去引导学生观察分析谢尔宾斯基三角形的变化,并从中探究数列的递推公式和通项公式,传递自然、连贯贴切,现场课堂表现出学生参与度高,课堂气氛融洽,师生精神状态良好,真正实现了师生互动,突显了学生的主体地位。
=4,bn=bn-1+3n-1(n≥2),bn+1=4bn-3bn-1(n≥2)等的几何背景,学生从谢尔宾斯基三角形的一系列变化中观察出了数列中项数的变化及其各种关系。具体讲,从探究图中绿色三角形个数的计数问题自然过渡到对图中绿色、黑色三角形总个数的计数问题探究。这种从不同视角去引导学生观察分析谢尔宾斯基三角形的变化,并从中探究数列的递推公式和通项公式,传递自然、连贯贴切,现场课堂表现出学生参与度高,课堂气氛融洽,师生精神状态良好,真正实现了师生互动,突显了学生的主体地位。
参考文献
[1]教育部.普通高中数学课程标准(实验)[S].北京:人民教育出版社,2003
[2]人民教育出版社,课程教材研究所,中学数学课程教材研究开发中心.普通高中课程标准实验教科书(数学A版必修5)[M].北京:人民教育出版社,2006.
[3]张维忠.文化视野中的数学与数学教育[M].北京:人民教育出版社,2005
【注释】
[1]本文发表于《中学数学教学参考》2009年第9期(中旬),作者:段春炳,张维忠。
[2]本文作者:李福军,张维忠。
[3]本文作者:王利庆,张维忠。
[4]本文发表于《中学数学杂志》2011年第8期,作者:王才洪,张维忠。
[5]本文发表于《中学数学教学参考(初中)》2007第10期;《中国人民大学复印报刊资料・中学数学教与学(初中)》2007年第12期全文转载了此文。作者:吴伟英,周均华。
[6]本文发表于《中学数学杂志(初中)》2008年第10期,作者:徐初晓,徐玉蓉,周均华。
[7]本文发表于《中学数学杂志(初中)》2007年第6期;《中国人民大学复印报刊资料・中学数学教与学》(初中)2008年第3期全文转载了此文。作者:金益洪,胡艳。
[8]本文发表于《中学数学教学参考》2009年第5期(上旬),作者:吕峰波,张维忠。
[9]本文发表于《中学数学教学参考》2008年第8期(上旬),作者:郑日锋,张维忠。
[10]本文发表于《数学教学研究》2010年第3期,作者:吕峰波,张维忠。
[11]本文作者:舒卫军,张维忠。
[12]本文发表于《数学教学》2009年第2期,作者:李芳,马玉斌,张维忠。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















