对江西年高考压轴题的几点思考

对江西2010年高考压轴题的几点思考

扶呈现

2010年普通高等学校招生全国统一考试江西卷第22题是

证明以下命题:

①对任一正整数a，都存在正整数b，c(b＜c)，使得a²，b²，c²成等差数列;

②存在无穷多个互不相似的三角形△n，其边长a_n，b_n，c_n为正整数且成等差数列。

作为压轴题，本题有很大的难度或技巧，几乎所有的成绩好的考生都认为不知从何下手，就是很多学生和老师看到标准答案都觉得技巧性太强，拼凑性强，答案来得很突然，仿佛在云雾之中。

证明:(试题标准答案)

(1)易知1²，5²，7²成等差数列，则a²，(5a)²，(7a)²也成等差数列，所以对任一正整数a，都存在正整数b= 5a，c= 7a，(b＜c)，使得a²，b²，c²成等差数列;

(2)若，成等差数列，则有＿＿=＿＿

选取关于n的一个多项式，例如4n(n²－1)，使得它可以按两种方式分解因式，由于4n(n²－1)=(2n－2)(2n²+2n)=(2n+ 2)(2n²－2n)

因此令

易验证a_n，b_n，c_n满足①，因此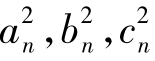成等差数列，

当n≥4时，有a_n b_n c_n，且a_n+ b_n－c_n= n²－4n+ 1＞0

因此以a_n，b_n，c_n为边长可以构成三角形，将此三角形记为△_n(n》4)其次，任取正整数m，n(m，n≥4，且m≠n)，假若三角形△_m与△_n相似，则有:

。据比例性质有:

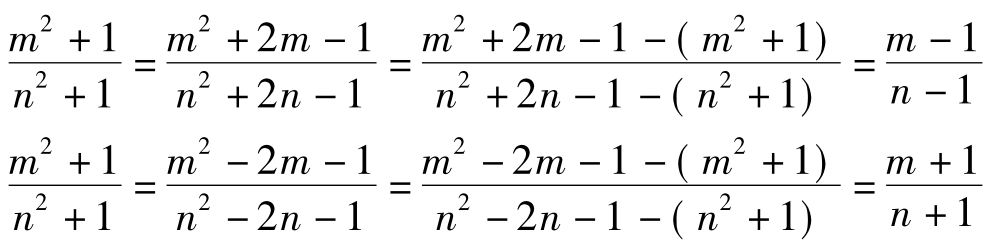
所以，由此可得m= n，与假设m≠n矛盾。

即任两个三角形△_m与△_n互不相似。所以存在无穷多个互不相似的三角形△_n，其边长a_n，b_n，c_n为正整数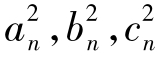，成等差数列。

这种证法留给我们两个问题:

第一，“易知1²，5²，7²成等差数列”，是不易知的。学生的感觉是验证容易发现难，没有头绪。本题解答忽略了一个关键性的问题，你是怎么发现该数组的?还有没有其他的数组?

第二，第2问中“选取一个多项式，例如4n(n²－1)，使得它可按两种方式分解因式，——”不太好理解，特别是“令”的两式必须求出的b_n是一致的，有很强的拼凑感，不具有推广性。

实际上，由a²，b²，c²成等差数列，设a=1，则有2b²=1+ c²，得c²=2b²－1，故c²为奇数，c为奇数，设c= 2k+1(k∈N₊)，→b²=2k²+2k+1= k²+(k+ 1)²，

问题转化成求满足该式的一组毕达哥拉斯数(或称勾股数组)，取k= 3→b²= 3²+ 4²=5²→b= 5，c=7。故有1²，5²，7²成等差数列。

这当然不是唯一的数组，此问题更深的研究要用到数论的一个性质，

定理一:若m，n互素且m＞n，(k∈N₊)，设x= kmn，，则x，y，z构成毕达哥拉斯数。(即满足x²+ y²= z²的所有正整数解)证明略。

由该定理当k= 1时得到的一些勾股数组如下表:(列出一部分)

考虑到x，y为连续自然数，故x=20，y= 21，z= 29，为满足题意的勾股数组，即可得: b²=20²+21²=29²，→b=29，c= 2×20+1=41。这就得到第二个成等差数列的数组:1²，29²，41²成等差数列。

再继续，可用下面的定理:

定理二:在定理一中，设，则x，y为连续正整数的一个必要条件为:2＜t＜1+，或。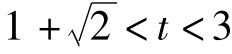

限于篇幅，证明略。

由定理2可使寻找连续数组的过程简化，并得到第三组数:1²，169²，239²成等差数列。第四组数:1²，985²，1393²．成等差数列等。

对于第2问，可由成等差数列，则，可设

a_n= An²－Bn+C，c_n= An²+ Bn+C(A，B，C∈Z)，则:

则只需［A² n⁴+(2AC+ B²)n²+C²］为完全平均数，即△= 0→B²+ 4AC= 0，此时b_n= An²－C。

令A= 1，C=－1，→B=2，→可得标准答案中的a_n，b_n，c_n。

若令A=1，C=－4，B=4，则可得另一组a_n，b_n，c_n。事实上可以得到无数组。以下证法相同。

通过上面的研究，我们揭开了题目的面纱，弄清了问题的本质，我们也得到了更一般或更易理解的解法和结论。但我们的研究不能就此为止，事实上在第1问中，我们给出了四组数组，那么是否有无穷多组呢?这是一个新问题，我们可以进一步去探讨。