教学中引导学生“巧思妙解”——谈谈“胡政铨放缩公式”的应用
段兴仁
教学中,教师要鼓励学生结合具体问题,进行大胆的尝试、猜想、联想,引导学生能从多角度思考问题,做到“多思”出“多解”,“多解”出“巧解”,使学生的智慧在丰富多彩的数学活动中得以“闪光”,从而培养学生思维的灵活性和创造性。
九江一中2010届高三(16)学生胡政铨同学在学习数列型不等式的证明中,巧思出一个让人耳目一新的放缩方法,我把其称为“胡政铨放缩公式”,现介绍如下:
一、胡政铨放缩公式:
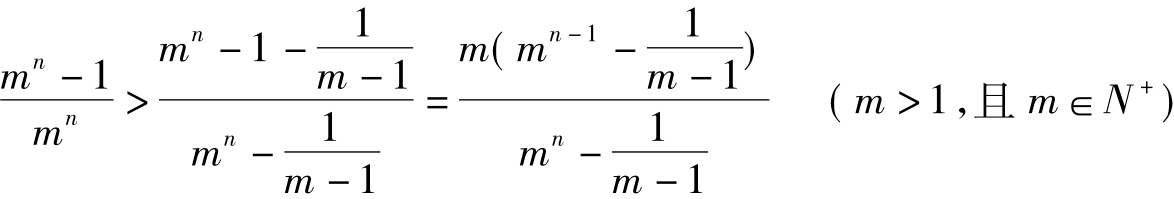
二、理论依据:
分式性质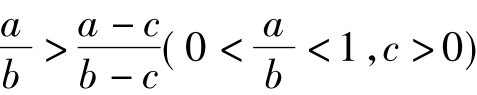
三、应用:
例1 已知: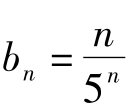 ,
,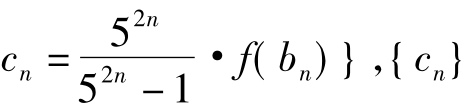 的前n项之积Tn,(n∈N*)
的前n项之积Tn,(n∈N*)
求证: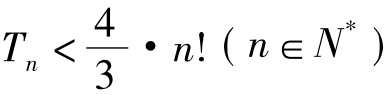
分析: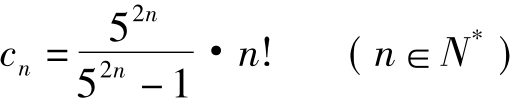
分析: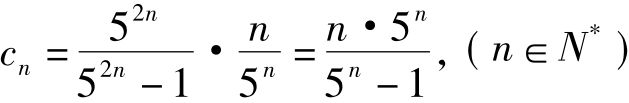
要证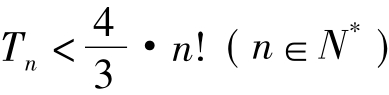
只需证明: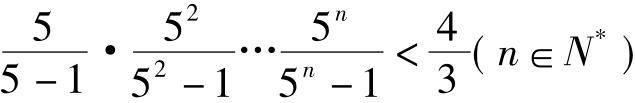
即证: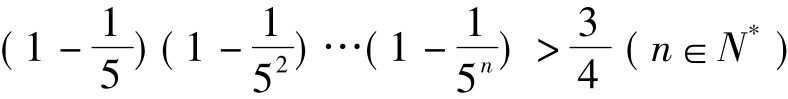
常用方法:先用数学归纳法证明一个加强命题:
(1+ x1)(1+ x2)(1+ x3)…(1+ xn)≥1+(x1+ x2+ x3+…+ xn)(1+ xn>0,n∈N*)
即证: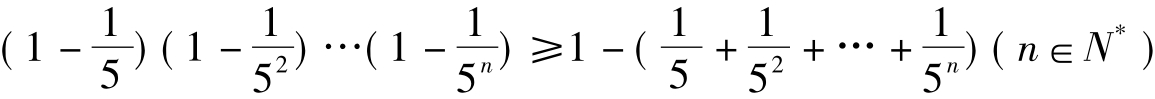
(数学归纳法证明过程略)
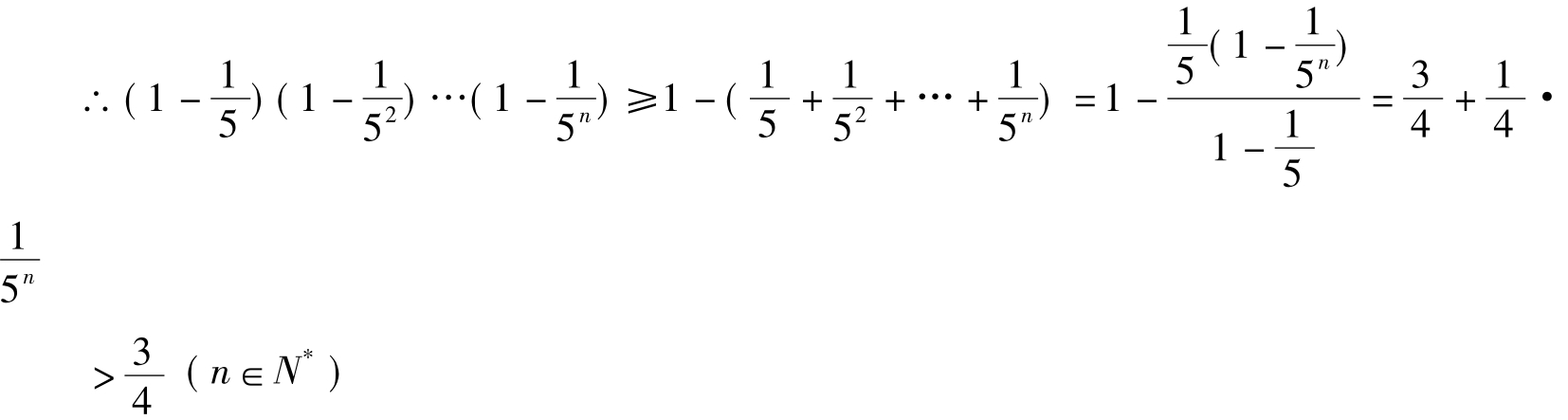
利用胡政铨放缩公式:
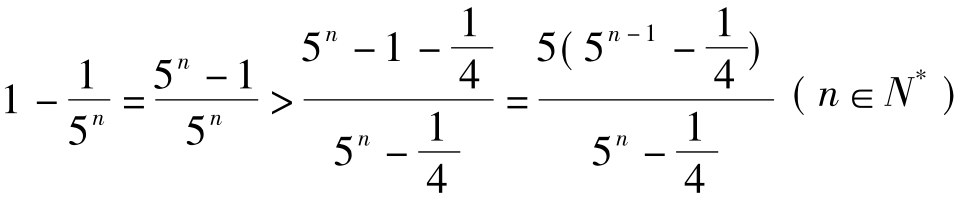
再相消
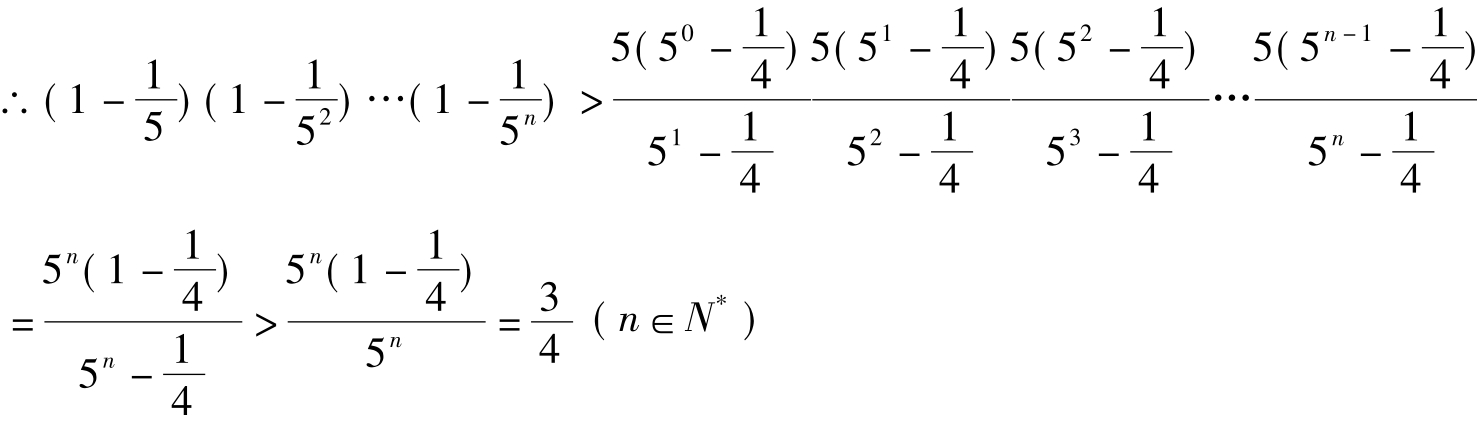
例2 (2006年江西卷22)已知数列{an}满足: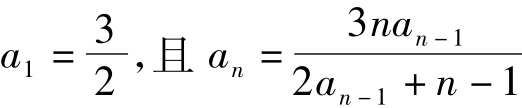 (n≥2,n∈N*)
(n≥2,n∈N*)
(1)求数列{an}的通项公式;
(2)证明:对于一切正整数n,不等式a1·a2·…a〈n 2·n!
参考答案的解法:(1)将条件变为: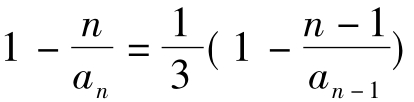 ,因此{1-
,因此{1-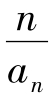 }为一个等比数列,其首项为
}为一个等比数列,其首项为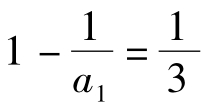 ,公比
,公比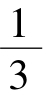 ,从而
,从而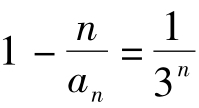 ,据此得
,据此得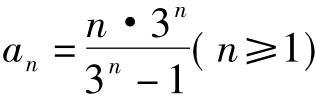
(2)证:据1°得,a1·a2·…an=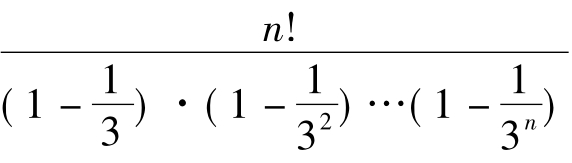
为证a1·a2·…a〈n 2·n!
只要证n∈N*时有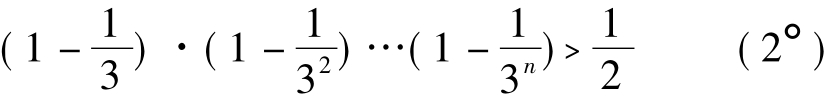
方法一:左端每个因式都是正数,先证明,对每个n∈N*,有
![]()
用数学归纳法证明3°式:
(1)n=1时,3°式显然成立,
(2)设n= k时,3°式成立,
即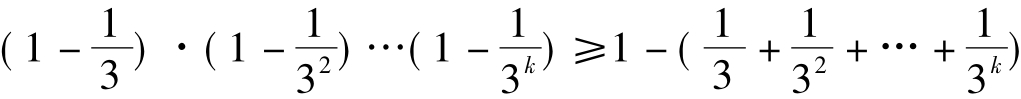
则当n= k+1时,
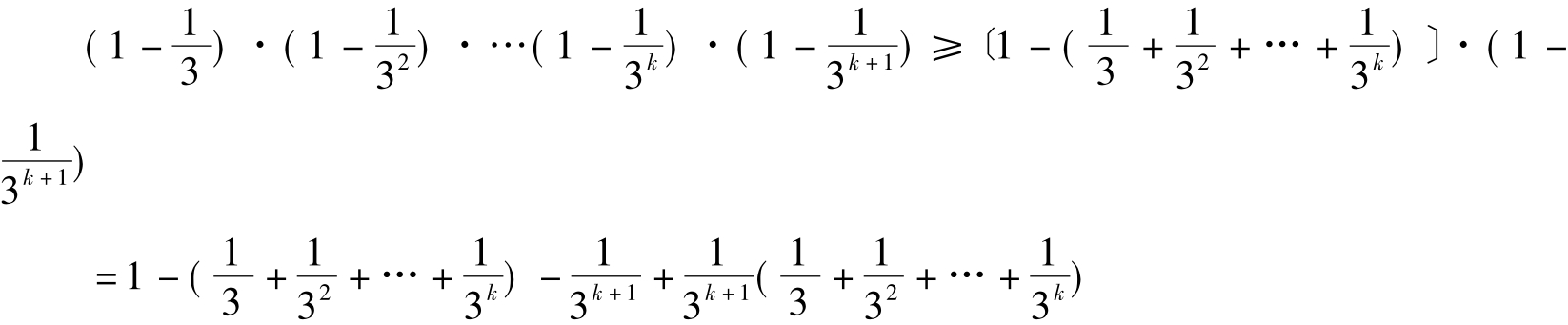
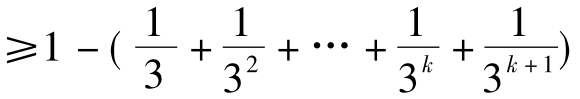 即当n= k+1时,3°式也成立。
即当n= k+1时,3°式也成立。
故对一切n∈N*,3式都成立。
利用3°得,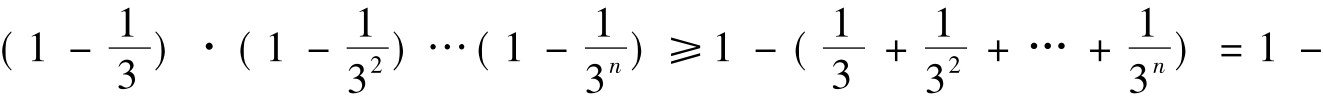
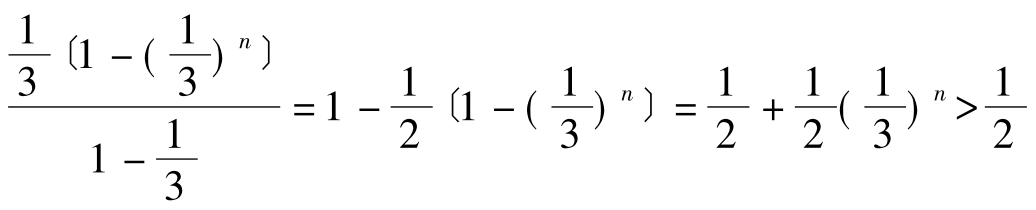 故2°式成立,从而结论成立。
故2°式成立,从而结论成立。
方法二:拼凑成相消形
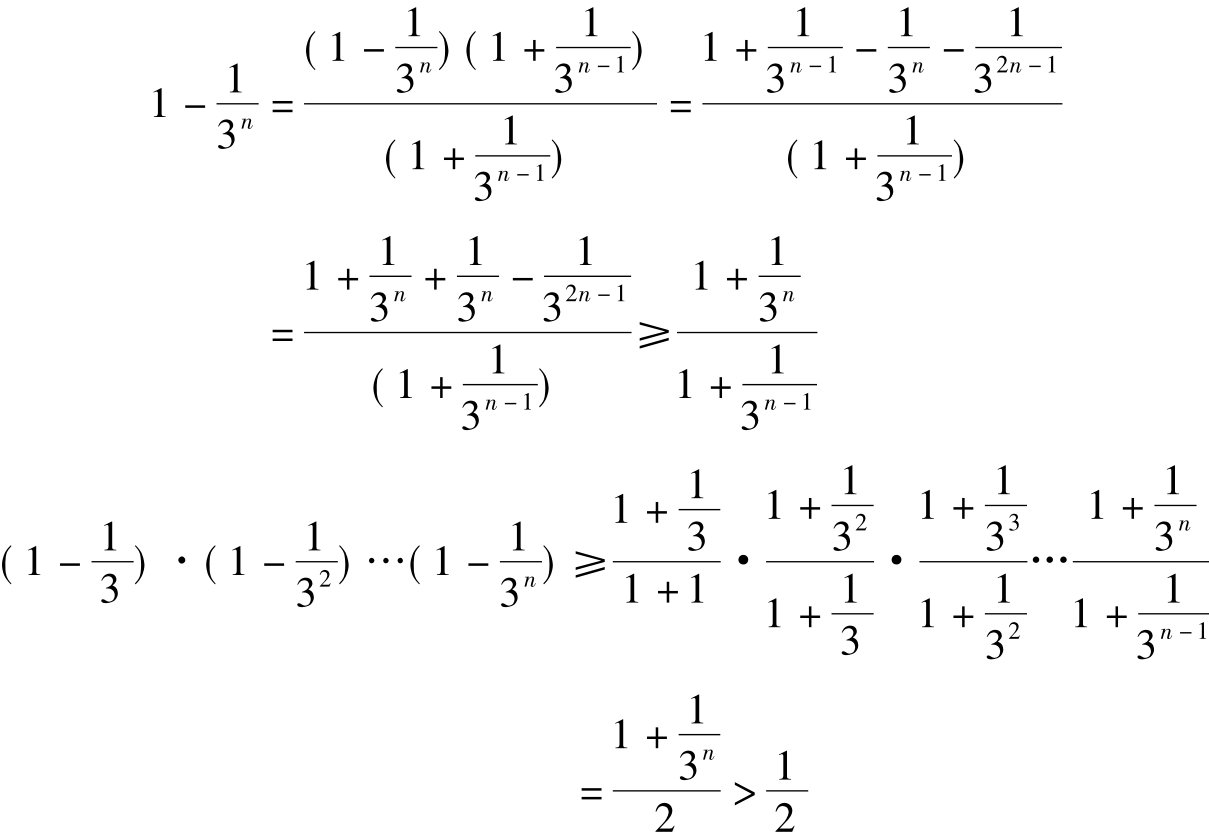
方法三:利用胡政铨放缩公式,则另有一番美好的滋味
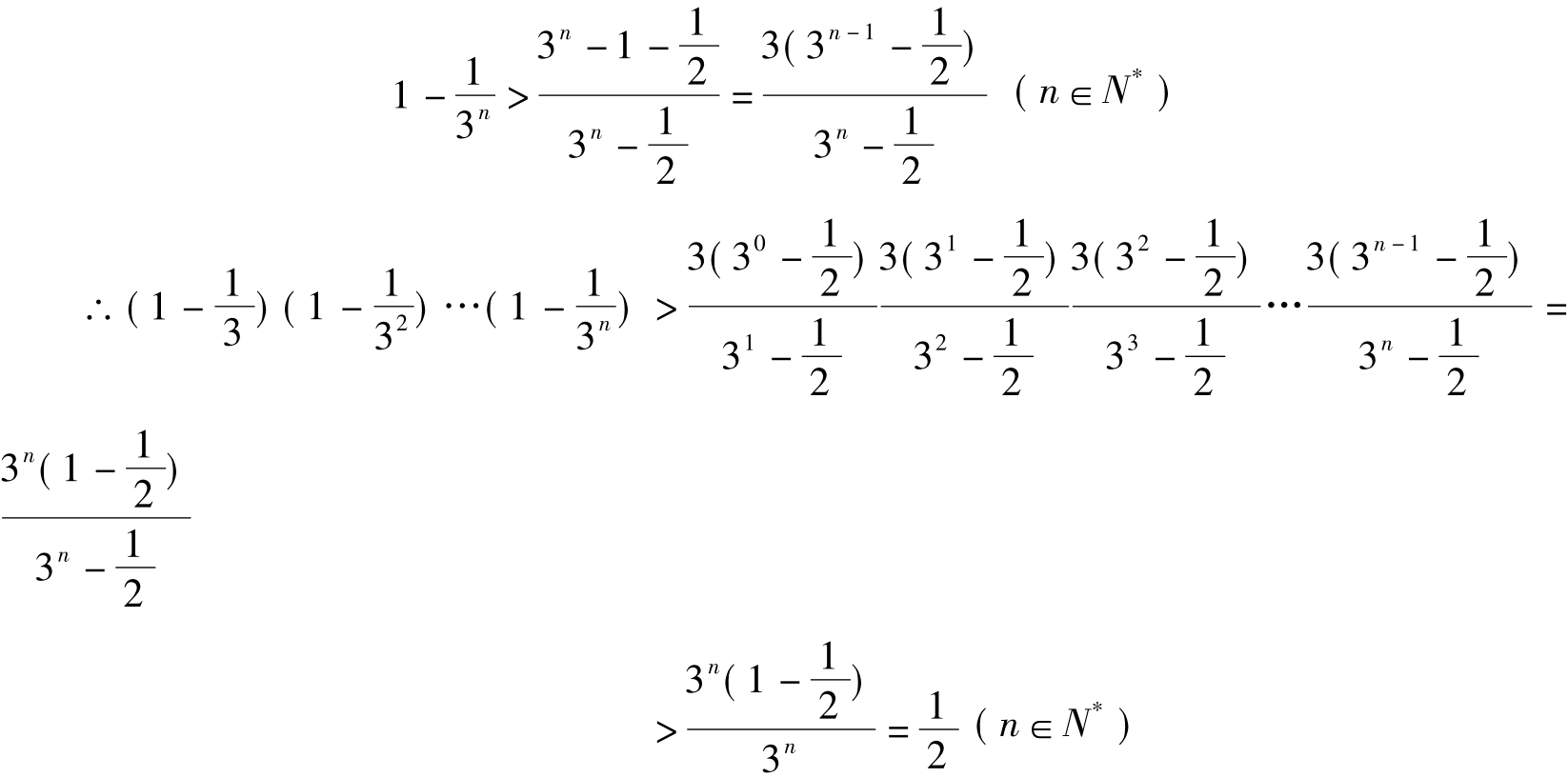
例3 已知: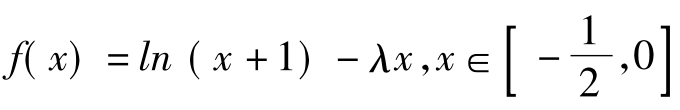
(1)当λ= 2时,求证:f(x)≥0
(2)若f(x)≥0对于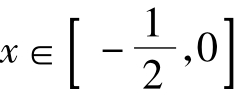 恒成立,求实数λ的取值范围;
恒成立,求实数λ的取值范围;
(3)求证: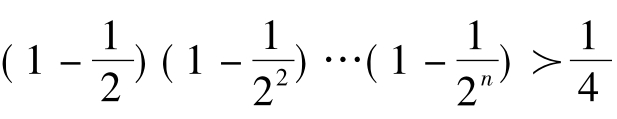
解:(1)当λ= 2时,f(x)= ln(x+ 1)-2x,f'(x)=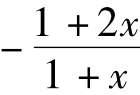 ≤0对x∈
≤0对x∈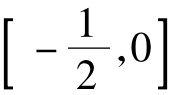 恒成立。∴f(x)≥f(0)=0
恒成立。∴f(x)≥f(0)=0
(2)①x∈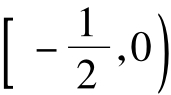 时,f(x)≥0→λ≥
时,f(x)≥0→λ≥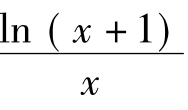 ,记h(x)=
,记h(x)=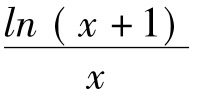
则h'(x)=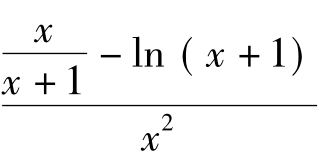 ,再记g(x)=
,再记g(x)=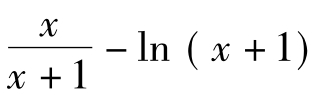 ,则
,则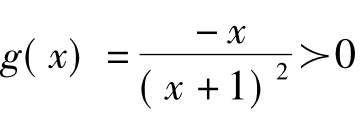
∴g(x)<g(0)=0,∴h'(x)=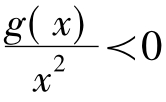 ,∴h(x)在
,∴h(x)在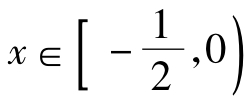 单调递减,
单调递减,
∴λ≥h(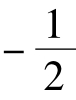 )= 2ln 2
)= 2ln 2
②当x=0时,f(x)≥0恒成立,∴λ的取值范围为[2ln 2,+∞)
(3)、由(2)知,当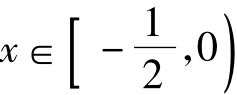 时,ln(x+ 1)≥(2ln 2)x
时,ln(x+ 1)≥(2ln 2)x
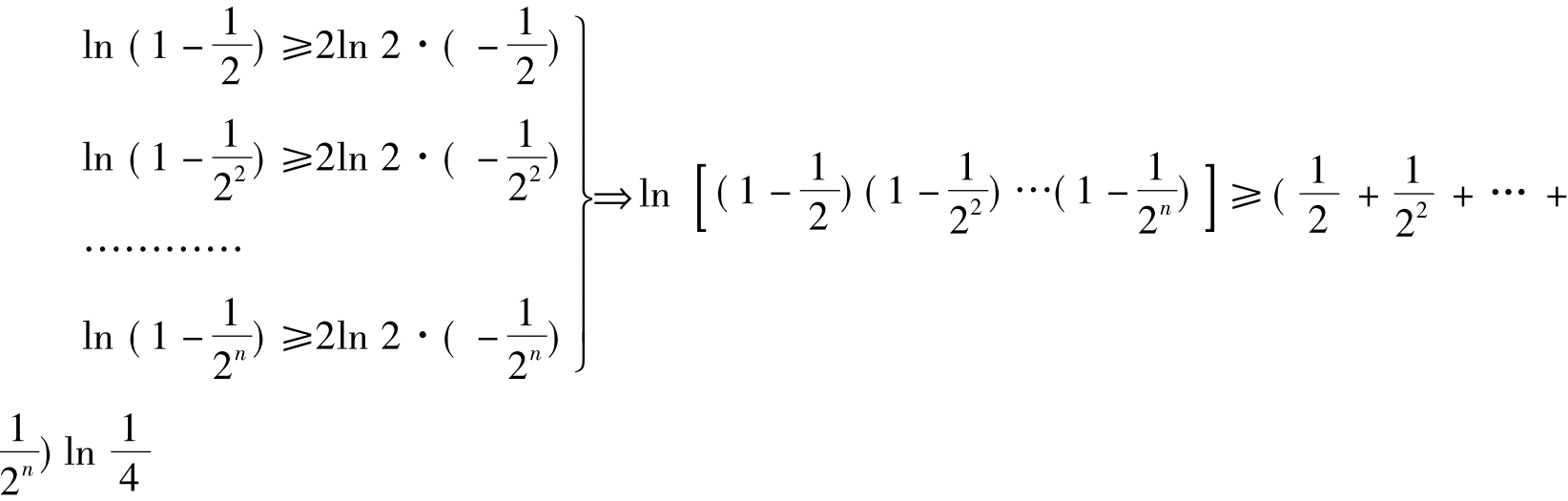
又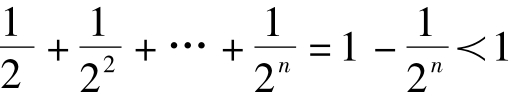 ,而ln
,而ln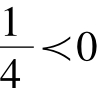 故即证
故即证
最佳途径:利用胡政铨放缩公式
![]()
再相消
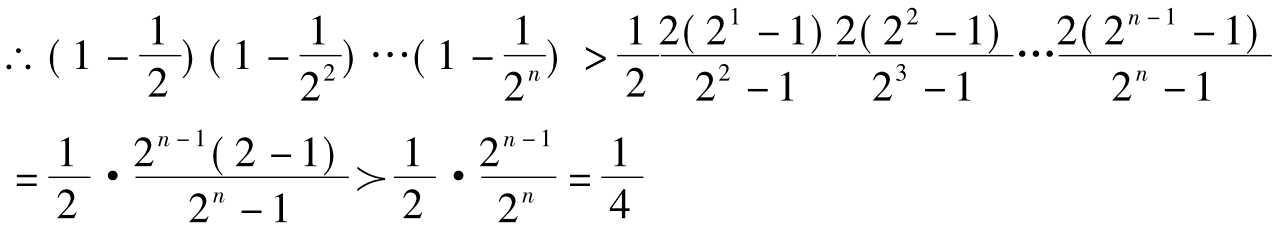
(原载《中学数学教学参考》2011年2月下旬)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

















