三角形“四心”向量形式的充要条件及其应用

三角形“四心”向量形式的充要条件及其应用

祝　兵

在高考中，往往将“向量作为载体”对三角形的“四心”进行考查。本人对三角形四心向量形式的充要条件进行归纳，觉得她们形式优美、对称，遂整理出自己的一点心得体会。下面从个几方面加以阐述:1．三角形的“四心”定理;2．第一组三角形“四心”定理向量形式的充要条件及其证明;3．第二组三角形“四心”定理向量形式的充要条件及其证明;4．与三角形的“四心”有关的一些常见的向量关系式。

1．三角形的“四心”定理

内心:三条角平分线的交点，也是三角形内切圆的圆心。

性质:到三边距离相等。

外心:三条中垂线的交点，也是三角形外接圆的圆心。

性质:到三个顶点距离相等。

重心:三条中线的交点。

性质:三条中线的三等分点，到顶点距离为到对边中点距离的2倍。

垂心:三条高所在直线的交点。

性质:此点分每条高线的两部分乘积相等。

2．第一组三角形的“四心”定理的平面向量表达式及其证明

(1)O是ΔABC的重心

(2)点O是ΔABC的垂心

(3)点O是ΔABC的外心

(4)O是的内心ΔABC的内心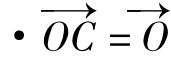(其中a，b，c是ΔABC三边)

①G是ΔABC的重心

证明:充分性:若

则

以为邻边作平行四边形OADC

设OC与AB交于点P，则P为AB的中点，有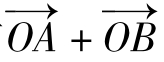

得

即O，C，P，D四点共线，故CP为ΔABC的中线，同理，AO，BO亦为ΔABC的中线，所以，O为的重心。

必要性:如图，延长OC与AB于P，则P为AB的中点，由重心的性质得

②点O是ΔABC的垂心

证明:O是ΔABC的垂心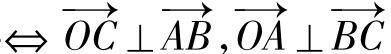

同理故当且仅当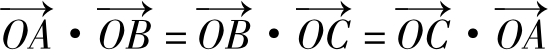

③点O是ΔABC的外心

证明:点O是ΔABC的外心

(O为三边垂直平分线的交点)

④O是ΔABC的内心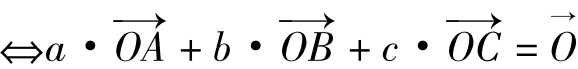(其中a，b，c是ΔABC三边)

证明:充分性:

所以，而分别是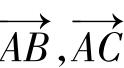

方向上的单位向量，所以向量

平分∠BAC，即平分∠BAC，同理平分∠ABC，得到点O是ΔABC的内心。

必要性:若点O为ΔABC的内心，延长AO交BC于P，

由三角形内角平分线的性质定理，

有，

于是

再由

有代入前式中便得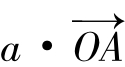

3．第二组三角形的“四心”定理的平面向量表达式及其证明

(1)O是ΔABC的内心

(2)O是ΔABC的重心

(3)O是ΔABC的外心

(4)O是ΔABC的垂心

证明:设O是ΔABC内任一点，以O为坐标原点，OA所在直线为x轴，建立直角坐标系。

并设A(p，0)，B(q cosα，sinα)，C(r cosβ，－r sinβ)，其中∠AOB=α，∠AOC=β

显然不共线，由平面向量基本定理，可设则

(1)若O是ΔABC的内心，则S_ΔBOC:S_ΔAOC:S_ΔAOB= a:b:c

故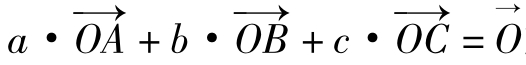或

(2)若O是ΔABC的重心，则S_ΔBOC=S_ΔAOC= S_ΔAOB=

故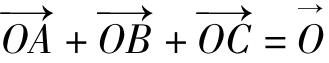

(3)若O是ΔABC的外心

则S_ΔBOC:S_ΔAOC:S_ΔAOB= sin∠BOC:sin∠AOC:sin∠AOB= sin∠2A:sin∠2B:sin∠2C

故

充分性的证明:O是ΔABC的外心

(同一法)设0'为ΔABC的外心，则

则∴O与O'重合即O为外心。

(4)若O是ΔABC(非直角三角形)的垂心，

则S_ΔBOC:S_ΔAOC:S_ΔAOB= tan A:tan B:tan C

故

证明:OC sin A(A、E、O、F四点共圆)同理

因此只需证

OB·OC·cos A=OA·OB cos C=OA·OC cos B

先证第一个等式

OB·OC·cos A=OA·OB cos C(E、C、D、O四点共圆，∠C，∠AOE为∠DOE的补角;E、O、F、A四点共圆，∠A，∠COE为∠FOE的补角)所以上式成立，即第一个等式成立。同理可证:该连等式成立，原题得证。

充分性的证明:O是ΔABC(非直角三角形)的垂心，

(证明方法同一法)，证明参考外心充分性的证明。

4．与三角形的“四心”有关的一些常见的向量关系式

例1　已知O平面上一定点，A、B、C是平面上不共线的三点，动点P满足，λ∈(0，+∞)，则动点P的轨迹一定通过△ABC的(　　)

A．外心　　B．内心　　C．重心　　D．垂心

分析:如图设都是单位向量

易知四边形AETF是菱形　　故选答案B

例2　设O是平面上一定点，A、B、C是平面上不共线的三点，动点P满足，λ∈(0，+∞)，则动点P的轨迹一定通过△ABC的(　　)

A．外心　　B．内心　　C．重心　　D．垂心

分析: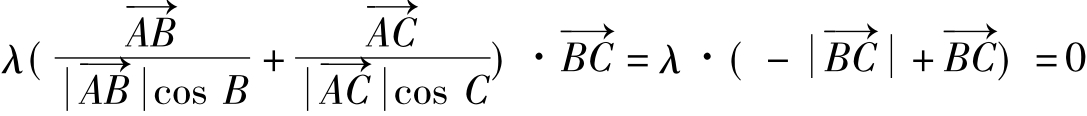　　故选答案D

例3　已知O是平面上一定点，A、B、C是平面上不共线的三个点，动点P满足:，则P的轨迹一定通过△ABC的(　　)

A．外心　　B．内心　　C．重心　　D．垂心

答案:C

例4　ΔABC的外接圆的圆心为O，两条边上的高的交点为H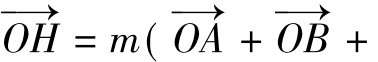，，则实数m=＿＿。

解:作直径BD，连DA，DC，有，DA⊥AB，DC⊥BC，AH⊥BC，CH⊥AB，故CH//DA，AH//DC

故AHCD是平行四边形，进而

故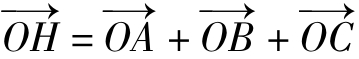，所以m= 1

例5　已知向量与满足且，则△ABC为(　　)

A．三边均不相等的三角形　　B．直角三角形

C．等腰非等边三角形　　　　D．等边三角形

解析:非零向量与满足，即角A的平分线垂直于BC，

∴AB=AC，又，所以△ABC为等边三角形。

答案为D

例6　已知向量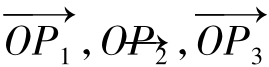满足条件=1，

求证:△P₁ P₂ P₃是正三角形。

证明:由已知，两边平方得，

同理，从而ΔP₁ P₂ P₃是正三角形。

反之，若点O是正三角形ΔP₁ P₂ P₃的中心，则显然有且，即O是ΔABC所在平面内一点，且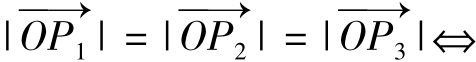点O是正ΔP₁P₂P₃的中心。

参考文献:

崔景南，朱永厂．对一道向量习题的探究．数学教学，2007(5)