导数在高中物理概念和解题中的应用

导数在高中物理概念和解题中的应用

柯　尧

一、导数的概念

简单地说，y对x的导数就是y对变量x的变化率，数学形式:。在函数图像中，导数表示图线在该点切线的斜率(图1)。

图1

高中物理中，很多物理量都是通过比值的形式定义，如密度，速度等等，而比值即表示一个量对另一个量的平均变化率。

二、导数在物理概念中的应用

1．速度。速度表示物体位移对时间的变化率，用导数形式可以表示为。课本通过平均速度引入瞬时速度的概念，通常学生理解比较困难，主要是因为他们之前很少接触极限的思想。导数在求解某些复杂问题中的速度时比较简洁。举两例说明:

例1　河岸上的人以v₀匀速拉船靠岸，河岸高h，计算当船离岸距离x时船的速度。

图2

简析:如图2，建立一维坐标系，船的位置可以表示为:，

根据速度的定义，

又有绳子的收缩速度为v₀，

即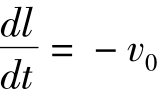，代入可得船的速度为:v=－v₀。

虽然此题利用沿绳的方向的速度大小相等来求解可能较方便，但是如果换成更难的情景，这种方法会更有效。

例2　摆长为l的摆做小振幅的振动，振幅为A，计算其振动过程的最大速度。

简析:先用常规方法来解:设单摆摆动过程最大摆角为θ，则A= lθ，

联立可得:。

现在利用速度的导数定义来求解，单摆做简谐运动的振动方程为:x= A sin(wt+φ)，

其中，

利用速度的定义式，因此最大值为。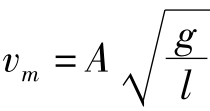

以上两种方法对比起来，第一种方法虽然能考查学生很多方面的能力，但是并不是每一个学生都具备这种能力，在讲解此题时，为了拓宽学生的解题思路，两种方法都应该提到。

2．加速度。加速度表示速度对时间的变化率。可以表示为:。

举一例说明其应用:课本上在推导匀速圆周运动的向心加速度表达式时所用的方法学生理解起来比较困难，因为其中用到了一些近似，让学生感觉结果不够可靠，但是如果采用下列方法，则比较理想。

图3

如图3建立直角坐标系，则质点的运动方程可表示为:x= r cos wt，y= r sin wt，为了求加速度，对分位移分别求二阶导数:

将加速度分解到切向与法向:

切向分量:a_τ= a_x sin wt+ a_y cos wt= 0，

法向分量:a_n= a_x cos wt+ a_y sin wt= rw²，

刚好与课本上匀速圆周运动的向心加速度表达式一致。

三、感应电动势

感应电动势等于磁通量对时间的变化量的负值，可以表示为。

课本推导正弦交变电动势的方法很麻烦，对于一些理解能力较差的学生掌握起来比较困难，并且自己很难第二次推导出来，若能用下面方法来推导会比较简单。设线框从位于中性面开始计时，经过时间t，

磁通量为:φ₁=BS cos wt

再过时间Δt(Δt→0)，磁通量为:φ₂= BS cos w(t+Δt)，

利用法拉第电磁感应定律:，

根据三角函数的和差化积:，

当Δt→0时，e为时刻t的瞬时电动势，由近似计算上次可写成:

e=NBSw sin wt。

上述推导过程就是导数的思想，等价于:。

4．电场强度。电场强度等于场强方向的电势的变化与位移的比值的负值，。

在很多参考书中有这样一个题目:

图4

例3　空间某一静电场的电势在x轴上分布如图4所示，x轴上有B、C两点，下列说法正确的是(　　)

A．E_Bx＞E_cx

B．E_Bx的方向沿x轴正方向

C．电荷在O点受到的电场力在x方向上的分量最大

D．负电荷沿x轴从B移到C的过程中，电场力先做正功后做负功。

简析:此题如果用常规方法分析也可以得出正确答案，但是比较麻烦，还要花上很长的时间，如果能够利用进行分析，很容易得出正确的答案。

还有很多其他的物理概念可以利用导数来定义，比如:牛顿第二定律的微分形式F=;场力与势能的关系;电流强度等。教师如果能对这些很熟悉，将会有利于自己对概念的透彻理解。

四、导数在求最值问题中的应用

某点导数在图像中表示的几何意义为图线在该点切线的斜率。由图像可知，在斜率(即导数)为0的地方，函数值对应最大或最小值。因此在求一些问题的最值时，令导数为0，就可以求出相应的最值。下面看两例:

例4如图5所示，一半径为R的圆盘绕水平轴匀速旋转边缘速度为，轮边缘有水滴从各位置甩出，求轮边缘抛出的水滴上升的最大高度及相应的抛出点位置。

简析:由抛体运动规律有:

Q点高度为，为了求h的最大值，令，求得最终结果。

例5　(09全国1)材料的电阻率ρ随温度变化的规律为ρ=ρ₀(1+αt)，其中α称为电阻温度系数，ρ₀是材料在t= 0°C时的电阻率。在一定的温度范围内α是与温度无关的常数。金属的电阻一般随温度的增加而增加，具有正温度系数;而某些非金属如碳等则相反，具有负温数系数。利用具有正负温度系数的两种材料的互补特性，可制成阻值在一定温度范围内不随温度变化的电阻。已知:在0°C时，铜的电阻率为1．7×10^－8Ω·m，碳的电阻率为3．5×10^－5Ω·m，在0°C时，铜的电阻温度系数为3．9×10–3°C^－1，碳的电阻温度系数为－5．0×10^－4°C^－1。将横截面积相同的碳棒与铜棒串接成长1．0 m的导体，要求其电阻在0⁰ C附近不随温度变化，求所需碳棒的长度(忽略碳棒和铜棒的尺寸随温度的变化)。

图5

简析:如图6设两部分导体长度分别为L₁、L₂，电阻分别为R₁、R₂;

图6

根据电阻定律有:，

总电阻，

因为总电阻不随温度变化，必有，

将ρ=ρ₀(1+αt)代入得，

且L₀= L₁+ L₂，解得:L₁=3．8×10^－3m。

点评:这道题应该说难度不大，但它需要学生把题意理解清楚，并且也牵涉到了很多量之间的转化，很多学生在运算中出了问题，采用上述这种方法，不但思路清晰，过程也很简洁。

结语:虽然高考中对微积分不作要求，但是如果我们教师自己平时能多用微积分的相关知识来思考一些问题，这将有利于对一些基本概念的理解。同样在物理概念和习题教学中，如果能给学生讲授一些如何利用微积分的知识去解决物理问题，这将能大大地激发学生学习物理的兴趣，让他们感觉到物理学的奥妙，同时能体会到数学这门基础学科的作用，这也符合新教材更重视数学方法在物理中的应用的思想。特别是现在高校组织的自主招生的考试，有很多题目的难度较大，知识面更广，这就要求我们的教学内容能上升到更高的高度。

(2011年江西省物理学会年会上被评为一等奖)