数学作文的写作

三、数学作文的写作

（一）回顾展示型

当一段时间的学习结束，教师可以让学生回顾一下数学学习的情况，尤其是解决重点、难点问题的学习过程，从中选择自己最感兴趣、印象最深的一点，有时甚至于一节课师生的共同讨论与研究，学生用手中的笔将当时的思维过程叙述出来、展示出来。甚至包括在解题过程中所走的弯路，中间经过的曲折，如自己的思维怎样受阻，随后又怎样突破自己的思维局限，最后使问题获得了解答。这样写出来的文章可读性很强，其他的学生还可从中受益。与此同时，教师还可以了解学生掌握知识的情况，从而改进自己的教学。

（二）总结归纳型

当学生学完某一方面的内容，教师可以让学生以数学作文的形式总结、归纳自己的学习成果，并在今后的数学学习活动中加以运用，这比由教师简单、机械地传授学习方法更有意义。经过学生再创造，认识会更加深刻，理解会更加深入。如一位学生对“函数定义域的求法”做了如下总结。

1．已知函数y=f（x），求其定义域。

（1）如果f（x）是整式，那么函数的定义域是实数集R；

（2）如果f（x）是分式，那么函数的定义域是使分母不等于零的实数的集合；

（3）如果f（x）是偶次根式，那么函数的定义域是使根号内的式子不小于零的实数的集合；

（4）如果f（x）是由几个部分的数学式子构成的，那么函数的定义域是使各部分式子都有意义的实数的集合（即使每个部分有意义的实数的集合的交集）

例1：求下列函数的定义域．

例2：求函数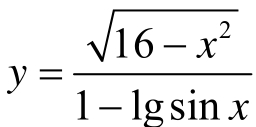的定义域。

解：

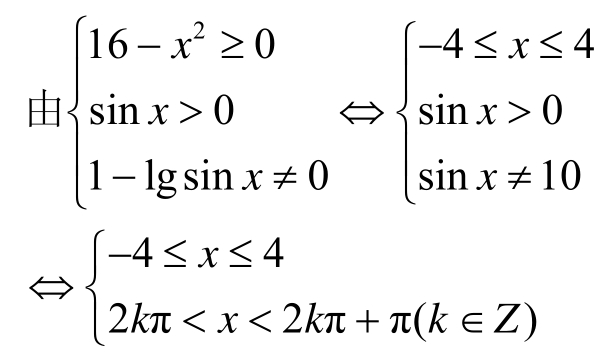
⇔−4≤x＜−π，或0＜x＜π

所以原函数的定义域为{x|−4≤x＜−π，或0＜x＜π}。

2．已知函数y=f（x）的定义域，求复合函数y=f [g（x）]定义域。

若已知函数y=f（x）的定义域x∈[m,n]，则在求复合函数

y=f [g（x）]定义域时，应抓住函数f [g（x）]的意义，“以g（x）充当原函数f（x）中的自变量x而得到y=f [g（x）]”。即由m≤x≤n，就有m≤g(x)≤n，解此不等式，便得复合函数定义域y=f [g（x）]定义域。所以复合函数y=f [g（x）]定义域为：{x|m≤g(x)≤n}。

例3：若函数f（x）的定义域为[0,4]，求f(x²)的定义域。

解：令t =x²，则f（t）与f（x）的定义域相同，

所以，0≤x²≤4，即−2≤x≤2。

所以，原函数的定义域为：[−2,2]。

例4：若函数f（x）的定义域为[0,1]，求g(x)=f(x+a)+f(x−a)的定义域(a≤0)。

解：由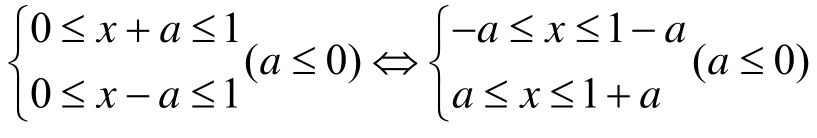

从而g（x）的定义域为[−a,1−a]I[a,1+a]。

Qa≤0，∴−a≥a，1+a≤1−a

（1）当a=0时，g（x）的定义域为[0,1]。

（2）当0≠a时：

①当a＜−a＜1+a＜1−a即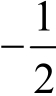＜a＜0时，g（x）的定义域为[−a，1+a]

②当a=1+a即a=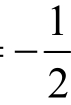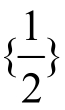时，g（x）的定义域为。

（3）1+a＜−a≤1−a即a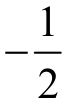＜时，g（x）不存在。

3．已知复合函数y=f[g（x）]的定义域，求函数y=f（x）的定义域。

若已知复合函数y=f[g（x）]的定义域为[m，n]，则在求函数y=f（x）的定义域时，应抓住“以x充当f[g（x）]中的g（x）而得到y=f（x）”。即由m≤x≤n，得到g（x）的取值范围，就是f（x）的定义域。所以，函数y=f（x）的定义域为：{x|x=g(t),t∈[m,n]}=。

例5：已知函数f(2^x)的定义域为(4,3)−，求函数y=f（x）的定义域。

解：43x−＜＜Q

∴2⁻⁴＜2^x＜2³，即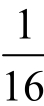＜2^x＜8

所以，函数y=f（x）的定义域为(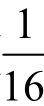,8)。

这不正是一篇非常优秀的数学作文的展示吗？你想学生经过如此这般的思考，对问题的理解会不深入吗？

（三）探究发现型

在数学教学过程中，教师要根据学生的年龄特征和认知水平，设计探索性和开放性的问题，多给学生一些自主探究的机会。当学生经过探究，发现、解决了某一数学问题，发现了某一数学规律，教师应热情鼓励，引导学生用笔记录下来，让学生享受成功的快乐。

又如，在《“m项式”的展开式——“二项式定理”的推广》（许绍甫）中，把二项式定理中的“二项式”推广到“三项式”，进而推广到一般的“m项式”，得出了相应的展开式，研究了展开式的项数、展开式系数的性质，最后介绍了“m项式”的展开式在概率中的应用。把平面杨辉三角推广到空间的三棱锥。

1．三项式的展开式

命题：对于任意的正整数n有：(a+b+c)ⁿ=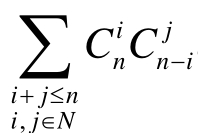a^n−i−jbⁱc^j=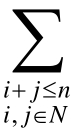T(i,j)a^n−i−jbⁱc^j_n

2．三项式系数的性质

性质1：T_n(i,j)=T_n−1(i,j)+T_n−1(i−1,j)+T_n−1(i,j−1)这条性质可视为“杨辉三角”推广到“三维空间”。

性质2：三项式系数具有（轮换）对称性，即T_n(i,j)=T_n(j,i)。

性质3：三项式系数的总和等于3ⁿ。

性质4：沿等边三角形上的任意一条线（边或网格）来看，越往中间的对应的点相应的三项式系数越大；反之，则越小。线上对应的中间点相应的三项式系数在该线上最大。

推论1：等边三角形不同线的中间点距此三角形的中心越近，则它对应的值就越大；反之，就越小。

推论2：如果三角形的中心是三项式系数的对应点，那么中心的对应值为三项式系数中的最大值；如果三角形的中心不是三项式系数的对应点，那么中间覆盖它的最小三角形的三个顶点对应的三项式系数相等，且为三项式系数中的最大值。

这就是不折不扣的学生的理解，是学生自己建构的“数学意义”，因为它赋予了学生的体验，蕴涵了学生的智慧，与单纯的“形式化”训练下的“双基”相比，它更具有生命气息与生命活力，更富有发展和成长的意义；它是满含学生情感的“双基”，是学生能够用而且愿意用的“双基”，是学生生活的“双基”。

（四）求异创新型

培养学生的创新意识和实践能力是素质教育的核心内容。在数学教学过程中，教师要尊重学生的创造性，鼓励学生求异创新。当学生在数学学习活动中有了新颖独特的解题方法、与众不同的解题思路，如果让学生写下来，就是一篇有价值的数学作文。有时学生的思维真是超出了我们老师的想象。

例如，在《最短路线问题的两种解法、应用及推广》（尹敏）一文中，给出了以下结论：

题型1：规则矩形网格的最短路线问题。

结论1：对于m×n阶矩形格（m，n分别为竖线和横线数，且m，n≥2），点A到点B的最短路径数等于杨辉三角中对应的直线m和n交叉处的数字，此数字可用组合数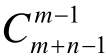表示。

结论2：在n×n阶矩形格中，点A到点B的最短路径数等于杨辉三角的中轴线上的数字。若在mn×阶矩形格中，点A到点B的最短路径数等于两边数字分别为m、n的V字型的顶点处的数字。

结论3：m×n型网格中被分成pq×和(m−p)×(n−q)矩形网格中的最短路线的条数是。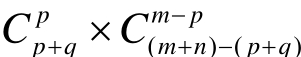

结论4：在一个由m×n个矩形组成的道路网格中，不经过m×n矩形网格被分成pq×和(m−p)×(n−q)矩形网格处的点，从矩形的一个顶点走到对角线的另一个顶点的最短路线有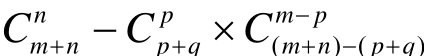条。

数学作文提出后，很受学生的欢迎，每年都有数十名学生的优秀数学作文被我们归纳成集，成为素质教育改革的一道独特风景线！