课时教学设计样例

二、课时教学设计样例

课时教学设计一：

全日制普通高中必修1第一章第三节（数学2009届学生提供的修改稿）

◆教学课题

§1.3.1　单调性与最大（小）值（第一课时）

授课对象：高一学生　　授课类型：新授课

◆教材分析

本节课位于数学必修1第一章第三节——函数的基本性质的第一课时，主要学习函数的单调性。函数的单调性是函数的重要性质。从知识的网络结构上看，函数的单调性既是函数概念的延续和拓展，又是后续研究指数函数、对数函数、三角函数的单调性等内容的基础，在研究各种具体函数的性质和应用、解决各种问题中都有着广泛的应用。函数单调性概念的建立过程中蕴涵诸多数学思想方法，对于进一步探索、研究函数的其他性质有很强的启发与示范作用。

◆教学目标

（一）知识与技能

（1）从函数图像的角度，直观认识函数的单调性；

（2）从函数解析式的角度，学会运用数学符号表示函数的单调性，理解增减函数的定义；

（3）运用定义证明函数的单调性。

（二）过程与方法

通过观察一些函数图像的升降，形成增（减）函数的直观认识。再通过具体函数值的大小比较，定量分析增（减）函数，认识函数值随自变量的增大而增大（减小）的规律。从图形语言到数学语言，将“数”与“形”有机结合，得出增减函数的定义，掌握用定义证明函数单调性的基本方法与步骤。

（三）情感态度价值观

学生经历从具体到抽象、从特殊到一般、从感性到理性的自主探究过程，体验数学概念的形成过程，培养学生善于观察、勇于探索的良好习惯和严谨的科学态度。

◆教学重难点

重点：形成增（减）函数的形式化定义，并能用定义解决简单的问题。

难点：形成增（减）函数的形式化定义的过程中，如何从图像升降的直观认识过渡到函数增减的数学符号语言表述；用定义证明函数的单调性。

◆教法学法

教法：启发探究式、问题驱动式

（基于学生的认知储备，就图像角度直观描述函数单调性的特征学生并不感到困难。困难在于，把具体的、直观形象的函数单调性的特征抽象出来，用数学的符号语言描述，这里需要教师以问题驱动的方式，引导学生进行积极的思维活动，主动参与知识的探究活动。）

学法：观察—猜想—推理—证明—应用

（学生通过对直观函数图像的观察，以描述性语言表述自己的猜想，并从定性到定量进行推理，数形结合加以证明，最后到巩固应用。培养学生“数学化”、“再创造”的学习方法。）

◆教学准备

将部分函数图像和文字说明做成幻灯片；借助几何画板制作函数图像，追踪点的轨迹，直观、便捷地展示函数的图像；将部分表格和图像以学习资料的方式发给每位学生，提高课堂效率。

◆教学导图

具体如图2-1所示。

图2-1　教学导图

◆教学过程

（一）创设情境，引入课题（5min）

【问题】你知道2008年北京奥运会开幕式时间为何要定在8月8日吗？

主要是天气的原因，北京的天气到8月中旬，平均气温、平均降雨量和平均降雨天数等均开始下降，比较适合举办大型国际体育赛事。

【设计意图】以学生熟悉并关注的话题引入新课，吸引学生的注意力，设置轻松的学习氛围。

【活动】图2-2是北京市2008年8月8日一天24小时内气温随时间变化的曲线图。

图2-2　2008年8月8日北京一天内气温随时间变化的曲线

教师引导学生识图，启发学生思考其中蕴含的信息，重点引导学生观察图像的升降情况，即函数的单调性，并列举生活中其他的数据变化情况。

【设计意图】体会研究函数单调性的必要性，明确本课我们要研究和学习的课题，同时激发学生的学习兴趣和主动探究的意识。

（二）步步探索，形成概念（18min）

1.借助图像，直观感知

【活动】观察一次函数f（x）＝x和二次函数f（x）＝x²的图像（见图2-3、2-4），研究函数图像的变化规律。

图2-3　f（x）＝x图像

图2-4　f（x）＝x²图像

学生观察函数图像，并发表自己的见解，体会同一函数在不同区间上“上升”与“下降”的变化差异。教师点拨引导，师生共同得到：不同的函数，其图像的变化趋势可能也不同；统一函数在不同区间上的变化趋势也不一定相同。函数图像的这种变化规律反映了函数的一个重要性质，即函数的单调性。

【设计意图】体会函数f（x）＝x与f（x）＝x²的图像升降规律，增强学生的直观感觉，为学习增减函数做认知铺垫。

2.定量分析，理性认知

【问题】如何描述函数图像的“上升”、“下降”呢？

【活动】以二次函数f（x）＝x²为例，列出x，y的对应值表（见表2-6）来研究它的上升与下降情况：

表2-6　三次函数f（x）＝x²的x、y对应值

对比函数图像与表格，引导学生从区间（—∞，0］和（0，＋∞）进行分析，可以发现：

图像在y轴左侧“下降”，也就是说，在区间（—∞，0］上，随着x的增大，相应的f（x）值反而随着减小；图像在y轴右侧“上升”，也就是说，在区间（0，＋∞）上，随着x的增大，相应的f（x）值也随着增大。

【设计意图】指导学生从定性分析到定量分析，从数值变化角度认识函数的单调性，将描述性语言转化为数学语言表示。这是学习增减函数的第一次认识提升。

3.抽象思维，形成概念

【问题1】如何利用函数解析式f（x）＝x²描述“随着x的增大，相应的f（x）随着减小”“随着x的增大，相应的f（x）也随着增大”？

【引导一】以区间（0，＋∞）为例，任意改变x₁，x₂的值，当x₁＜x₂时，都有x²₁＜x²₂吗？

学生随意给出一些（0，＋∞）上的x₁，x₂的值，当x₁＜x₂时，用计算器验证是否都有x²₁＜x²₂。

【引导二】我们验证的是一些具体的、有限个自变量的值，对于（0，＋∞）上任意的x₁，x₂，当x₁＜x₂时，都有x²₁＜x²₂吗？

学生思考教师提出的问题，并将自己的想法与同学交流。教师引导学生结合图形，得出：（图形语言）函数f（x）＝x²在（0，＋∞）上图像是上升的，用函数解析式来描述就是（符号语言）：对于（0，＋∞）上任意的x₁，x₂，当x₁＜x₂时，都有x²₁＜x²₂。（文字语言）即函数值随着自变量的增大而增大。具有这种性质的函数叫增函数。

【设计意图】通过限定区间，强调突出单调性描述中取值的“任意性”，从直观认识过渡到数学符号表示，获得学习增减函数的第二次认识提升。

【问题2】如何定义一个函数f（x）在某个区间D上为增函数呢？

【活动】学生讨论、交流，说出自己的想法，体现合作交流的学习方式；教师进行分析、点拨、评价，给出增函数的定义：

如果对于定义域I内某个区间D上的任意两个自变量的值x₁，x₂，当x₁＜x₂时，都有f（x₁）＜f（x₂），那么就说函数f（x）在区间D上为增函数。

图像表示（见图2-7）：

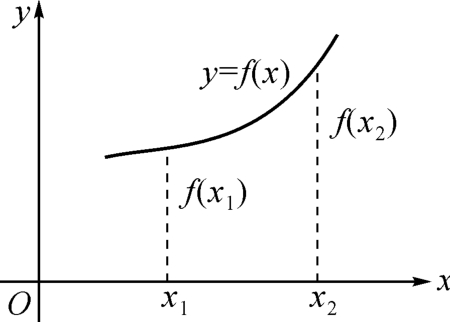
图2-7　增函数图像

【设计意图】由具体到一般引出增函数的定义，由形象到抽象，培养学生的逻辑思维能力。

【问题3】根据函数f（x）＝x²在y轴左侧图像是下降的，类比增函数的定义，由此你能概括出怎样的结论？如何给出减函数的定义？

【活动】由学生观察、验证、讨论、交流，并类比增函数的定义表述减函数的定义：

如果对于定义域I内某个区间D上的任意两个自变量的值x₁，x₂，当x₁＜x₂时，都有f（x₁）＞f（x₂），那么就说函数f（x）在区间D上为减函数。

图像表示（见图2-8）：

图2-8　减函数图像

【设计意图】培养学生的类比能力，完成增（减）函数的形式化定义，突破教学难点，获得学习增减函数的第三次认识提升。

4.辨析判断，深化理解

判断以下句子是否正确，为什么？

①函数f（x）＝x²在区间（—∞，＋∞）上是单调增函数。

②定义在R上的函数f（x）满足f（2）＞f（1），则函数f（x）在R上是增函数。

③若函数f（x）在区间（1，2］和（2，3）上均为增函数，则函数f（x）在区间（1，3）上为增函数。

【设计意图】

题①是为强调函数单调性是针对某一个区间而言的，是一个局部性质。有些函数在整个定义域内是单调的；有些函数在定义域内的部分区间上是增函数，在部分区间上是减函数；有些函数是非单调函数，如常数函数。

题②是为强调函数的单调性是函数在一个单调区间上的“整体”性质，x₁，x₂具有任意性，不能用特殊值代替。

题③是为说明函数在定义域内的两个区间A，B上都是增（或减）函数，一般不能认为函数在A∪B上是增（或减）函数。

（三）课堂练习，巩固提高（16min）

【练习1】如图2-9所示，是定义在闭区间［—5，5］上的函数y＝f（x）的图像，根据图像说出y＝f（x）的单调区间，以及在每一单调区间上，函数y＝f（x）是增函数还是减函数。

图2-9　练习1

【活动】以学生自学的方式学习此题，进一步理解增（减）函数的定义，教师巡视课堂，个别辅导，收集反馈信息，及时点评。

【设计意图】进一步加深对增（减）函数的认识，学习单调区间的概念，培养学生阅读自学的能力。

【练习2】物理学中的波利尔定律p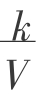＝（k是正常数）告诉我们，对于一定量的气体，当体积V减小，压强p将增大。试用函数的单调性证明之。

【活动】在教师的引导下，学生进行思考与讨论，并口述回答，教师进行板书演示，规范书写步骤。

分析：怎样来证明“体积V减小，压强p将增大”呢，根据函数单调性的定义，只要证明函数p＝（k是正常数）是减函数。怎样证明函数p＝（k是正常数）是减函数呢？只要在区间（0，＋∞）（因为体积V＞0）任意取两个大小不相等的值，证明较小的值对应的函数值较大，即

设V₁＜V₂，去证明p₁＞p₂.p（V₁）＞p（V₂）也就是只要证明p（V₁）—p（V₂）＞0。

证明：设V₁＜V₂，V₁，V₂∈（0，＋∞）.p（V₁）—p（V₂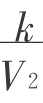）＝—。因为k是正常数，V₁＜V₂，所以＞0，p（V₁）＞p（V₂）。所以，体积V减小，压强p将增大。

最后，总结概括证明函数单调性的步骤：任意取值—作差变形—判断定号—得出结论

【设计意图】加强函数单调性的应用，形成解题思路，提高解题能力。

【练习3】画出反比例函数y＝的图像。

①这个函数的定义域I是什么？

②它在定义域I上的单调性是怎样的？证明你的结论。

【师生活动】教师：借助几何画板给出函数的图像，通过观察图像，引导学生对函数是否具有某种性质作出猜测，并模仿练习2的解题过程，进行独立分析与论证。

学生：相互讨论，尝试自主进行函数单调性的证明，可能会出现不知如何比较f（x₁）与f（x₂）的大小、不会正确表述、变形不到位或根本不会变形等困难。

师生：教师深入学生中，与学生交流，了解学生思考问题的进展过程，投影学生的证明过程，纠正出现的错误，规范书写的格式。最后，借助投影仪投影个别学生的解题过程，师生共同分析与探讨，强调分区间讨论函数的单调性。

完成解题后，点明从中渗透的探究函数性质的常用方法：通过观察图像，先对函数是否具有某种性质作出猜测，然后通过逻辑推理，证明这种猜想的正确性。

【设计意图】有效的数学学习过程，不能单纯的模仿与记忆，数学思想的领悟和学习过程更是如此。利用学生自己提出的问题，让学生在解题过程中亲身经历和实践体验，师生互动学习，生生合作交流，共同探究。并从中学习探究函数性质的方法，为研究其他函数性质提供方法依据。

（四）课堂小结，学习反思（5min）

【问题】这节课我们学了哪些内容？从中运用了哪些数学方法？

在知识层面上，引导学生回顾函数单调性定义的探究过程，使学生对单调性概念的发生与发展过程有清晰的认识，体会到数学概念形成的三个主要阶段：直观感受、文字描述和严格定义。

在方法层面上，首先引导学生回顾判断、证明函数单调性的方法和步骤；然后引导学生回顾知识探究过程中用到的思想方法和思维方法，如数形结合、等价转化、类比等，重点强调用符号语言来刻画图形语言，用定量分析来解释定性结果；同时对学习过程作必要的反思，为后续的学习做好铺垫。

【设计意图】让学生建构自己的知识网络，理解数学思想方法的应用。

（五）作业布置，巩固新知（1min）

必做题：教科书第39页习题1.3A组第1、2、3.

选做题：①证明函数y＝x³—b（b是常数）在R上是增函数。

②定义在（1，1）上的函数f（x）是减函数，且满足：f（1—a）＜f（a）。求实数a的取值范围。

【设计意图】分为必做题与选做题的目的在于服务不同的学生，分层提高。必做题是基础练习题，强化巩固函数的单调性应用，提高学生的综合运用能力；选做题是为学有余力的学生设置的，用于扩展知识面，提高解决问题的能力。

◆板书设计

课时教学设计二：

“合情推理”（第一课时）^[1]

（一）教学目标

【知识与技能目标】理解归纳推理的概念，了解归纳推理的作用，掌握归纳推理的一般步骤，会利用归纳进行一些简单的归纳推理。

【过程与方法目标】学生通过积极主动地参与课堂活动，经历归纳推理概念的获得过程，了解归纳推理的含义；通过欣赏一些伟大猜想的产生过程，体会并认识利用归纳推理能猜测和发现一些新事实、得出新结论；能初步掌握归纳推理的一般步骤；通过具体解题，进一步感受归纳推理的优缺点及其使用方法。

【情感态度与价值观目标】学生乐于主动探究、积极思考，欣赏合情推理的价值，认识到“大胆猜想、小心求证”的重要性，并受到数学文化、数学精神的熏陶。

（二）教学重点与难点

【重点】归纳推理的含义与作用。

【难点】利用归纳法进行简单的合情推理。

（三）教学过程

1.创设情境，引出课题

师：某市为了解本市的高中生数学学习状态，对四所学校做了一个问卷调查，其中有两个问题的统计数据如表2-4所示：

表2-4　问卷调查

根据这四所学校的情况，你能推测全市高中生对数学的印象吗？

【设计意图】既为归纳推理概念的形成埋下伏笔，也为学生数学观、数学学习观的转变埋下伏笔。

生：谈自己的认识与体会（绝大多数表示接受和认可表中的数据）。

师：你是用怎样的方式得出结论的？这个结论一定正确吗？

师生：得出推理的概念：由已知判断（前提）到新的判断（结论）。

师：显示少年侦探柯南、埃及金字塔、医生诊断病人的症状、中央气象台天气预报等4张图片，说明推理在现实生活中是到处存在的。

【设计意图】推理在生活中大量存在，我们需要从数学上作深入的研究。

2.顺其自然，解决问题

（1）由实例归纳出归纳推理的概念

师：请仔细分析、比较下列推理，说出其推理的方式与特点。

①由铜、铁、铝、金、银等金属都能导电，猜想一切金属都能导电。

②由三角形内角和为180°，凸四边形内角和360°，凸五边形内角和为540°，猜想凸n边形内角和为（n—2）・180°。

③地球上有生命，火星具有一些与地球类似的特征，猜想火星上也有生命。

④因为所有人都会死，苏格拉底是人，所以苏格拉底也会死。

【设计意图】让学生通过直观感知、观察分析、归纳类比对推理作出合理分类，并抽象概括出合情推理和归纳推理的概念，经历由浅入深、由易到难、由特殊到一般的思维过程。

师：给你们一列数，第一个数是2，第二个数是4，第三个数是6，第四个数会是什么呢？

师：集中显示下列4个推理，请学生归纳其特点，并得到归纳推理的概念。

生：得出归纳推理的概念，明确归纳推理的特点。

师：你能举出生活中和学习中归纳推理的例子吗？

（2）进一步认识归纳推理

师：介绍浙江省地图着色问题，再现四色猜想产生与探究的过程；再介绍相关历史，如1852年英国人弗南西斯・格思里为地图着色时发现了四色猜想，1976年美国数学家阿佩尔与哈肯在两台计算机上用了1200个小时完成了四色猜想的证明等。

师：观察下列等式：3＋7＝10，3＋17＝20，13＋17＝30，…，你能从中发现什么规律？

如果换一种写法呢？

10＝3＋7，20＝3＋17，30＝13＋17，…

师：你验证“偶数＝奇质数＋奇质数”对任何大于4的偶数成立吗？

师生互动：当正偶数比较小时，由学生直接验证，然后再由学生任意提出一些比较大的偶数，教师借助计算机软件马上把它分解为2个质数之和.

师：介绍哥德巴赫猜想，并用式子2n＝p₁＋p₂（n∈N，n≥3）表示；然后再介绍陈景润和陈氏定理2n＝p₁＋p₂・p₃。

（3）进一步感受和体会归纳推理的魅力与价值

师：把全班学生分成两组，一组举出生活中用归纳推理发现结论的例子，一组举出科学研究中用归纳推理发现结论的例子。

师：在学生举例的基础上，再举牛顿发现万有引力、门捷列夫发现元素周期律、植物的向光性等例子，并指出：应用归纳推理可以发现新事实，获得新结论；归纳推理是科学发现的重要途径。

（4）归纳出归纳推理的一般步骤及其注意点

师生：归纳推理的一般步骤：①观察分析；②发现规律；③检验猜想。

师：归纳推理得到的结论是否一定可靠？为什么？

师：介绍费马猜想：

①已知2²1＋1，2²2＋1，2²3＋1，2²4＋1都是质数，运用归纳推理你能得出什么样的结论？

②半个世纪后欧拉发现，2²4＋1＝4294967297＝641×6700417，说明了什么？

③后来人们又发现2²6＋1，2²7＋1，2²8＋1都是合数，你们又有什么样的想法？

师：这是一个“猜想—验证—再猜想”的过程，科学发现需要把大胆猜想与小心求证有效地结合在一起。

3.运用巩固，形成能力

例　已知数列｛a_n｝的首项a₁＝1，且有a_n＋1＝

（1）请用直接推理和归纳推理两种方法分别求这个数列的通项公式，并仔细比较这两种方法的优缺点；

（2）记S_n＝＋＋＋…＋，试求S_n。

【设计意图】第（1）小题要求学生用归纳推理和演绎推理两种方法解决，并比较这两种方法的优缺点；第（2）小题重在让学生感受归纳推理发现新事实、提供研究方向上的价值，并增强学生用归纳推理解决问题的意识和能力。

练习：任取两条平行直线l₁，l₂，在l₁上取三个点依次记作A₁，B₁，C₁，在l₂上任取三个点依次记作A₂，B₂，C₂。连接A₁ B₂，A₂ B₁，记交点为P；连接A₁ C₂，A₂ C₁，记交点为Q；连接B₁ C₂，B₂ C₁，记交点为H，你能发现什么规律？

【设计意图】为学生提供一个真实的、开放的数学问题，让学生进一步感受数学美和发现规律的喜悦，同时认识到只要做个有心人，发现规律并非难事。

4.回顾总结，提升认识

师：请从知识、方法、思维三方面谈本节课的收获。

师：请谈谈本节课的学习体会与心理感受。

师：合情推理是地球上最美丽的思维花朵之一。

5.拓展延伸，继续提高

（1）书面作业：课本第93页A组第1，2，3题.

（2）选做作业：

①登录网站（课后指定网站），选择两个猜想并探究其来源.

②如图2-10所示三角阵，从上往下数，第1次全行的数都为1的是第1行，第2次全行的数为1的是第3行，…，第n次全行的数都为1的是第____________行：第61行中1的个数是_________。

图2-10　三角阵

实践与思考

1.什么是学期教学计划与一节课教学设计？并叙述两者的主要区别。

2.自选中学数学教材中一节课的教学内容，书写一份完整的教学设计。

【注释】

[1]洪琼.“合理推理”（第一课时）教学设计.数学通报，2010（7）.