【摘要】:如概率原理在生物遗传学中的应用,立体几何中的正多面体与化学中的金刚石、二氧化硅、晶体硅、石墨等物质结构的联系,三角函数与向量在物理学中的应用等。因此我们在教学上述知识点时,可适时创设与相关学科联系的情境导入,从而强化数学的工具性、基础性,激发学生学习的积极性。又如,在讲解“正多面体”内容时,提出问题:请问甲烷CH4的分子结构是怎样的?
四、结合相关学科导入法
数学课程是学习物理、化学、生物、技术等科学的基础,它的诸多知识都与上述学科有着紧密的联系。如概率原理在生物遗传学中的应用,立体几何中的正多面体与化学中的金刚石、二氧化硅、晶体硅、石墨等物质结构的联系,三角函数与向量在物理学中的应用等。因此我们在教学上述知识点时,可适时创设与相关学科联系的情境导入,从而强化数学的工具性、基础性,激发学生学习的积极性。
例如在执教“充要条件”时,首先提出以下问题:如图5-9所示,观察在电路图①②③④中,研究命题p:“闭合开关A”、命题q:“灯泡B亮”的关系,接着引出两命题之间的四种关系与①②③④的对应。
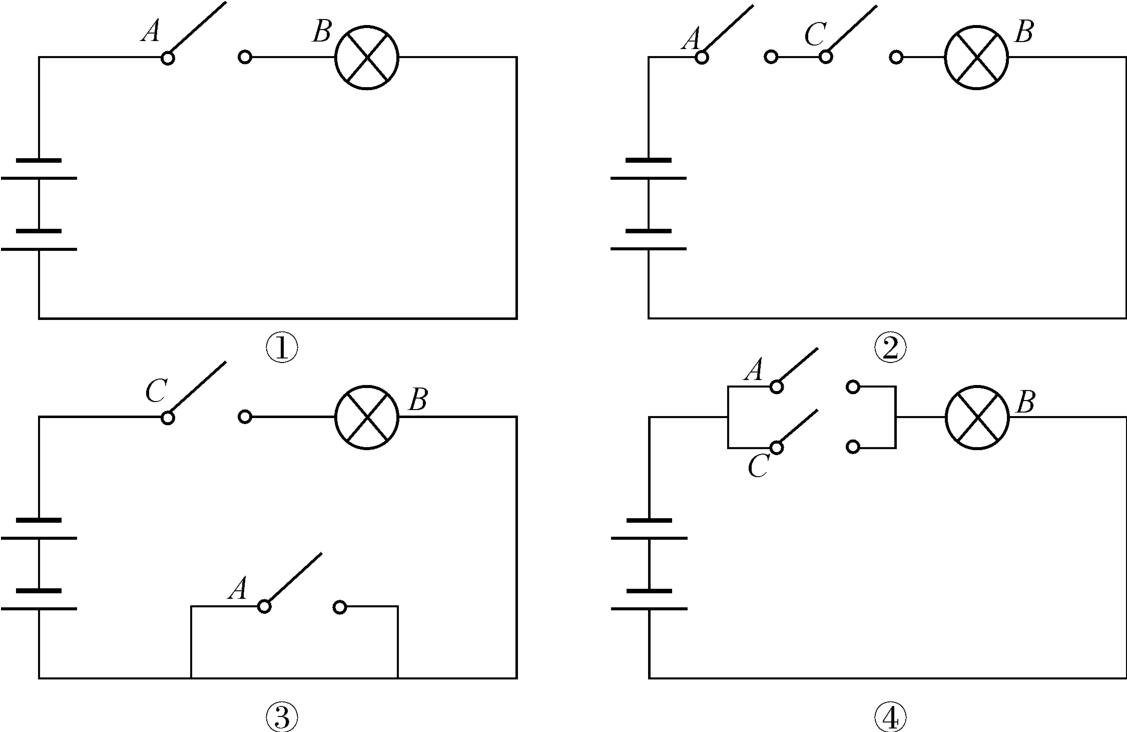
图5-9 电路图
引入图形后,学生的兴趣被有效地激活,教学效果也相当好,这真是“他山之石,可以攻玉”。
又如,在讲解“正多面体”内容时,提出问题:请问甲烷CH4的分子结构是怎样的?你能求出其中C—H键角的大小吗?
如图5-10所示,碳原子位于正四面体的中心,4个氢原子分别位于正四面体的四个顶点上。设碳原子与4个氢原子连成的四条线段两两组成的角为θ,则C—H键的键角的大小即为θ,易求得cosθ的值为- 。
。

图5-10 碳原子
当然,应用空间向量的知识也容易理解甲烷CH4为什么是非极性分子。
上述情境的创设不仅提高了学生的兴趣,而且从根本上搞清了问题的本质,因为理解的东西才有生命力。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















