一次考试引出的思考

一次考试引出的思考——浅谈如何讲解函数题中的参数

云浮市邓发纪念中学　吴江华

在高考复习第一轮复习的一次模拟考试中,试题中的两道题引起我的注意。一道题为:已知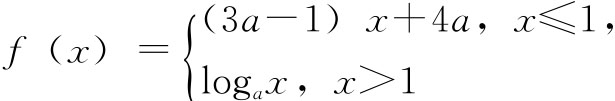是(-∞,+∞)上的单调函数,那么a的取值范围是_____。另一道是2007年广东省高考(理科)题的第20题:已知a是实数,函数f(x)=2ax²+2x-3-a,如果函数y=f(x)在区间[-1,1]上有零点,求a的取值范围。考试结果与我所料想的一样,很少有学生能正确解出。针对这种含参数的函数题出现频率较高,我作了比较详细的讲解,然后了解了学生的反应,很多学生都表示“这两道题并不难,但自己就是怎么想也想不出来,但当老师给出解答时,觉得这类题很普通,完全可以解出来。”为什么讲解之前、之后学生的反应会有这么大的区别呢？这个问题引起了我浓厚的兴趣,于是,我分析了学生错误的原因,大体分为以下几种:①思维混乱、完全不会做的学生比较少；②有一小部分同学主要是函数与方程的关系模糊不清；③大部分同学讨论了,但是把讨论的焦点集中到对称轴位置上,因情况太多,到后面不得不放弃。为什么出现这些错误呢？我通过调查总结了以下几种情况:有些同学对概念理解不深刻,只懂其表层的意思,不知道概念的内涵与外延。有些同学本身对这些题长期以来就有一些畏惧,像这种求函数中参数范围的题在初中就有,因为当时的知识水平的限制,很难理解讨论的缘由,时间一长,疑点越积越多,便对这种题型“敬而远之”了,还有不少同学在平时听课及做题时就不重视题目的解答过程,只重视结果,不反思,不能举一反三。还有的同学认为是老师在平时上课的时候在某些关键步骤说不清,道不明导致很多题学生知其然,而不知其所以然。当题目难度升级时,学生当然就不会做了。

那么高三教师在面对这类问题时,应该如何备考才能做到让学生在考试中应付自如呢？我觉得可以从以下几个方面尝试:

首先,在课堂上要运用数学思想来引导学生,由易到难,由模糊到清晰,逐步把思维的过程展示出来,让学生了解对参数的讨论的步骤一目了然。因此,我在讲解第二道题时,设计了这样的一个教学过程:

师:你以前做过这道题吗？

生:没有。

师:你做过这种类似的题吗？最近有吗？

经过一段时间后,有一学生站起来:前天上课有讲过一道这种这种类似的题:若关于x的方程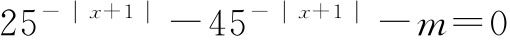有实根,求m的取值范围。

师:相似的地方在哪里？

生:换元后也是一个关于二次函数的零点问题,即方程根的问题。

师:还记得当时的处理方法吗？能把这种方法应用到这道高考题上吗？

生:有两种方法,一是利用二次函数的图象,得出不等式组；二是把参数和变量分离,把问题转化为二次函数的值域问题。

师(提示):大家不妨用这两种方法都试一试,看看能不能解出这道高考题？同学们大部分都在思考,埋头做起来了。

经过几分钟后,有学生站起来:老师,用二次函数的图象来做情况好复杂,应该如何分类才好？

师:这位同学问题提得好,在区间[-1,1]上有解的情况是比较复杂,首先二次函数有可能开口向上,有可能开口向下；有可能在区间[-1,1]有一个根,有可能在区间[-1,1]有两个根,也有可能二次函数与x轴相切,且切点在区间[-1,1]上。分类如果处理不好,计算量会增大,而且结果也不容易得出。有哪位同学能使分类最简便,更容易计算？

生:利用根的个数来分,分为在区间[-1,1]上有一个根和两个根,重根也记为两个根。这样计算很方便。这是我的解法:

解:函数y=f(x)在区间[-1,1]上有零点,即方程f(x)=2ax²+2x-3-a=0在[-1,1]上有解,a=0时,不符合题意,所以a≠0,方程f(x)=0在[-1,1]上有解有两种情况:

(1)方程f(x)=0在[-1,1]上只有一解⇔f(-1)·f(1)≤0⇔1≤a≤5。

(2)方程f(x)=0在[-1,1]上有二解⇔

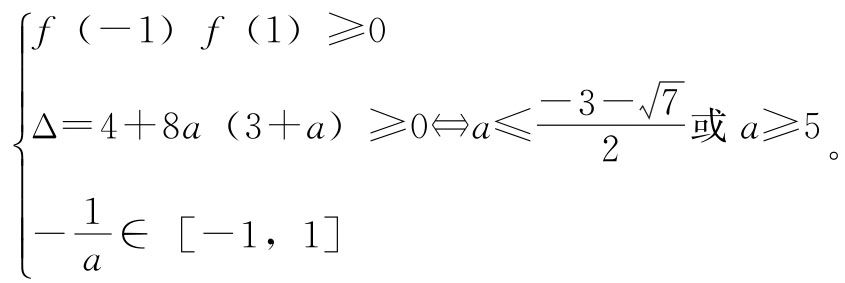
综上,所以实数a的取值范围是。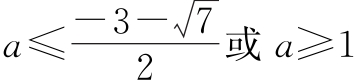

师(赞许):做得好。这样分类把计算量减少到了最低,又不会漏解。如果利用变量与参数分离,又会如何呢？

生:老师,这道高考题比上次讲的题目更复杂,参数与变量分离后,变量表示的函数比较复杂,难度较大。我只化简到这里:

解:a=0时,不符合题意,所以a≠0,又∴f(x)=2ax²+2x-3-a=0在[-1,1]上有解,⇔(2x²-1)a=3-2x在[-1,1]上有解)。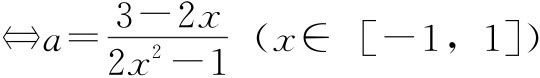

师:好,这是一个分式函数,上面是一次函数,下面是二次函数,这种函数的值域我们以前学过吗？

生:学过。

师:能不能用差别式法来求解？

生:不能,因为变量有范围,要用换元法。

师:对,下面大家按这种思想解下去。

生:因为用换元法要分子分母同时除以一个式子,所以我把函数倒过来求值域。请看:

解:a=0时,不符合题意,所以a≠0,又∴f(x)=2x²+2x-3-a=0在[-1,1]上有解,⇔(2x²-1)a=3-2x在[-1,1]上有解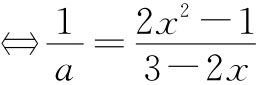在[-1,1]上有解,问题转化为求函数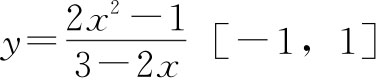上的值域；设t=3-2x,x∈[-1,1],则2x=3-t,t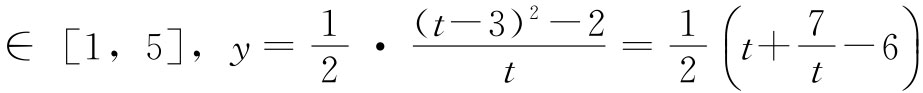。设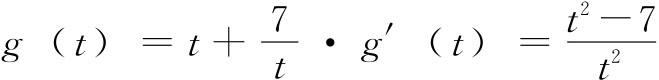,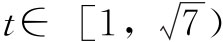)时,g′(t)＜0,此函数g(t)单调递减。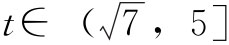时,g′(t)＞0,此函数g(t)单调递增,∴y的取值范围是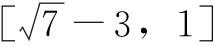。∴f(x)=2ax²+2x-3-a=0在[-1,1]上有解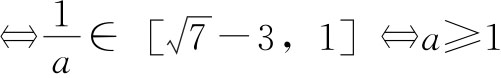或。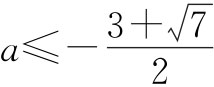

师:这位同学做得好。一是把参数和变量分离成功了,二是没有直接求参数a,而是求它的倒数,这是用换元法的解题过程中的需要；三是利用导数来判断单调性,没有利用基本不等式,因为利用基本不等式只能求出它的最小值,而无法求出最大值。

数学总是要从易到难,从简单到复杂,同时要让学生有一个接受的过程,让学生觉得问题的解决是自然的,思路不是从天而降的,而是从简单问题中得到启发的。在课堂教学中要做到这一点,这节课一定是成功的,因为教师让学生感受到了数学的简单美,不会觉得数学解题是遥不可及的事情。

其次,高三教师应让学生重视对数学基本概念理解。著名教育家布鲁纳认为:在有限的学习时间掌握对今后具有更大价值的知识,就必须掌握和发现各门学科的基本概念,基本原理和规律。现在高考题型浩如烟海且无法预测,那么我们高三教师能做的就是紧扣高考考纲,加强对基本知识概念的讲解,讲清其内涵与外延以及它所涉及的基本知识很方法。例如,我们在讲解函数的单调性时,我们不仅要让学生明白什么是增函数,什么是减函数？也要利用图形让学生明白函数连续性和单调性的关系,同时还要把这个抽象的概念具体到我们常见的函数中来,让学生充分明白影响这些函数单调性的关键量是什么,它是怎么样影响的？这些知识都弄懂了,凡是涉及单调性的题,学生就能较快找到突破口。例如第一道题:当x＞1时,y=f(x)是一个一次函数,而影响一次函数的单调性的量是一次项系数。当x＜1时,y=f(x)是一个对数函数,影响对数函数的单调性的量是底数。在联系单调性与连续性的关系。给出下列解答是不难的:已知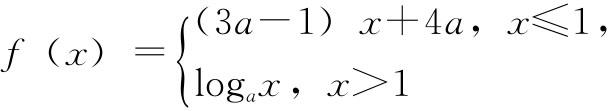是(-∞,+∞)上的减函数,那么a的取值范围是_____。

解:依题意,有0＜a＜1且3a-1＜0,解得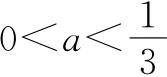,又当x＜1时,(3a-1)x+4a＞7a-1,当x＞1时,log_ax＜0,所以7a-1≥0解得。

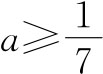数学概念是我们解题的核心所在,只有理解了数学概念,才能做到对问题的关键一目了然。理解数学概念要从各方面来理解,比如在本题中,运用数形结合也很容易得到正确答案。

最后,要注意举一反三、触类旁通。例如在讲解完第二道题后,可以布置以下作业:

(1)设f(x)=x²-2ax+2,当x∈[-1,+∞)时,f(x)≥a恒成立,求实数a的取值范围。

(2)设f(x)=x²-2ax+2,当x∈[-1,+∞)时,求y=f(x)的最小值。

(3)设f(x)=x²-2ax+2,当x∈[-1,+∞)时,y=f(x)的最小值为3,求a。

总之,从历届高考来看,因为求函数中的参数范围问题能很好地考察学生的思维能力,所以在高考试题中频频出现。如何帮助学生找到突破口并做到讨论时不重不漏,是高考复习中的一个重要环节。