知识生产函数估计

5．2．1 知识生产函数

本章在Hall［30］的研究基础上，以广义柯布-道格拉斯生产函数构建普通高校的知识生产函数：

Y＝ALαKβeu（5．1）

Y表示研究与开发的产出，R＆D产出用技术转让实际收入表示，R＆D资本投入用测量的R＆D资本存量来表示，R＆D劳动投入以技术活动人员数来表示。A表示R＆D投入的技术效率，L，K分别表示R＆D人员、R＆D资本存量，α，β分别表示R＆D资本投入和劳动投入的产出弹性。对式（5．1）进行对数化处理，得到：

ln Yit＝δ＋αln Lit＋βln Kit＋λ1Sit＋λ2Oit＋λ3Pit＋ui＋εit（5．2）

其中，δ表示常数项ln A；S表示出版论著数；O表示专利授权数，P表示绩效指标；t表示时间；i表示不同类别的高校；ui为非观测效应，表示不随时间变化的知识外溢效应；εit为特异性误差，表示随时间变化的知识外溢效应。除了本书重点观察的出版论著、专利授权数及绩效指标等对R＆D效率产生影响外，还有一些观测不到的影响因素：一类是不随时间而变化的知识外溢效应ui；另一类是随时间和产业而变化的知识外溢效应εit。假设高校按照成本最小化原则进行R＆D投入决策，那么，得到R＆D人员和R＆D资本存量投入的比例关系，即：

式（5．3）中的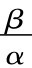表示按照折旧率计算后的真实资本存量R＆D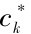；，cl分别表示R＆D资本存量的成本和R＆D人员的工资水平，反映了价格水平变动对R＆D资本存量的影响程度。利用式（5．3）可以估算出。按照Hall［25］的研究，反映R＆D资本价格水平的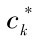（t）也存在折旧，并由下面的关系确定，即：

其中，Pk（t）表示价格水平，用固定资产价格指数表示；ρ表示资本的预期收益率，假定为10％。如果假定各年固定资产价格水平变动很小，那么利用式（5．3）、式（5．4）可以进一步得到：

通过对式（5．5）的估计，能够得到R＆D人员和R＆D资本存量的参数估计结果α，β，并利用式（5．3）、式（5．5），从而可以估算出折旧率。

在式（5．2）的估计中，本书采取GMM估计方法，从而可以有效地克服解释变量的内生性问题以及个体效应与解释变量的相关性问题。在模型设定上选择固定效应模型还是随机效应模型，使用Hausman检验来识别。

同时，估计的效应方程设定为：

ui＝λ1d1＋λ2d2＋λ3d3＋ωit（5．6）

人力资本存量：采用Halland Jones［26］基于Mincer公式计算教育回报率的方法计算人力资本存量，假设人力资本提高劳动力的效率，故有：

其中，φ（．）呈分段线性（piecewiselinear）形式 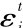示平均受教育年数，采用徐现祥和舒元［31］使用的受教育程度人口比重的权重，即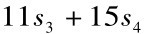s，si分别表示高校R＆D人员中文化程度是本科、硕士和博士人口所占的比重。

5．2．2 函数估计

估计知识生产函数所使用的数据与R＆D资本存量的估算数据相同，样本所包含的我国29个省及直辖市（不包括西藏自治区和新疆维吾尔自治区）104所985及211高等学校，其中38所985高校，66所211高校，时间跨度为2003—2013年，整体上为平行面板数据。

表5．1 全国104所普通高等学校样本名称

在知识生产效率的影响因素中，为了验证估计结果的可靠性，对于规模变量和产权结构变量分别使用了不同的指标。规模变量分别用高校技术转让平均收入来表示；质量变量分别用985，211高校专利授权数比重和985，211高校专利授权数平均论著数来表示。绩效变量用技术转让实际收入与R＆D投入之比来表示。本章所使用的变量及其定义见表5．2，对这些变量的描述性统计见表5．3。

表5．2 变量定义

表5．3 变量描述性统计（2003—2013年）

数据来源：《高等学校科技统计资料汇编》2002—2014。

对知识生产函数进行估计的目的是考察R＆D资本和劳动各自对产出的贡献以及知识生产过程的性质。以技术转让实际收入作为R＆D产出，建立技术转让生产函数模型。给定显著性水平为1％，Hausman检验支持随机效应模型。表5．4给出了知识生产函数的估计结果。R＆D资本和劳动对科研产出均有显著的影响作用，在知识生产函数模型及效率影响因素分析中，我们决定以随机效应模型作为分析的基础。

表5．4 知识生产函数及其影响因素的估计结果

注意：参数估计值下面括号中的数字为t检验值，、和分别表示参数估计值在1％，5％，10％显著性水平上显著。