直线相关与回归分析

（一）直线相关分析

直线相关是用相关系数来分析两变量间线性关系。相关系数是表达两变量线性相关程度和方向的一个指标，用r表示，其值在-1～+1之间。r＞0表示两变量是正相关，即一个变量的增加，另一个变量随之增加，r＜0表示两变量是负相关，即随一个变量的增加，另一个变量在减少；r=0表示两变量间不呈直线无相关；r越接近0，表示关系越不密切，r越接近+1或-1表示关系越密切。

CHISS的实现。点击：统计——统计推断——相关矩阵

实例：测得某地10名3岁儿童的体重与体表面积如下，试对该资料进行直线相关与回归分析。

体　重x（kg）　11.0　11.8　12.0　12.3　13.1　13.7　14.4　14.9　15.2　16.0

体表面积y（×103cm2）　5.283　5.299　5.358　5.292　5.602　6.014　5.830　6.102　6.075　6.411

解题步骤

（1）进入数据模块：此数据库已建立在CHISS\data文件夹中，文件名为：a6_1相关与回归.DBF。打开数据库。

点击：数据——文件——打开数据库表

找到文件名为：a6_1相关与回归.DBF——确认

（2）进入统计模块：进行统计计算。

点击：统计——统计推断——相关矩阵

反应变量：身高　体表面积——确认

（3）进入结果模块：查看结果。

点击：结果见表1-6-18。

线性相关（上三角为相关系数，下三角为P值），数据来自：C：\CHISS\Data\a6_1相关与回归.DBF

表1-6-18　线性相关分析结果

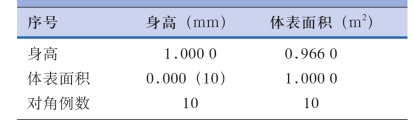
括号内为例数

（二）直线回归分析

直线回归是用回归方程来分析两变量间线性关系。直线回归是回归分析中最简单的形式。

CHISS的实现　点击：统计——统计推断——非参数方法——秩相关

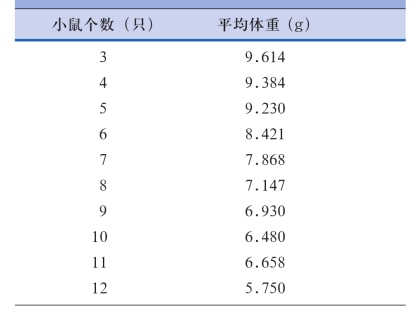
实例：Wainwright等（1988）在进行营养学实验前，先对小鼠体重与每窝小鼠只数间的关系进行了研究。从每窝分别为3只至12只的小鼠中，每个窝别大小随机抽取两窝。在出生后第32天测量不同窝别小鼠的平均体重，结果见表1-6-19。试作回归分析。

表1-6-19　不同窝别小鼠个数与小鼠平均体重

解题步骤

（1）进入数据模块：此数据库已建立在CHISS\data文件夹中，文件名为a6_2回归.DBF。打开数据库。

点击：数据——文件——打开数据库表

找到文件名为：a6_2回归.DBF——确认

（2）进入统计模块：进行统计计算。

点击：统计——多元统计——回归模型

解释变量：常数项、x

反应变量：y——确认

（3）进入结果模块：查看结果。

点击：结果见表1-6-20。

拟合线性模型，估计参数及检验结果（应变量=y）。

表1-6-20　拟合线性模型

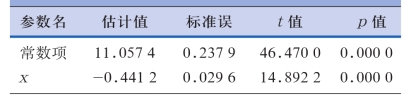
数据来自文件：C：\CHISS\Data\a6_2回归.DBF）

方差分析表（指标=y）见表1-6-21。

表1-6-21　方差分析表

（童新元）