二、应用直线相关与回归时的注意事项
1．对相关分析的作用要正确理解 相关分析只是以相关系数来描述两个变量间直线关系的密切程度和方向，并不能阐明两事物或现象间存在联系的本质；即使存在相关关系，也并不能说明是因果关系（相关关系中有的是因果关系，有的不是因果关系）。要说明两事物间的内在联系，必须凭借专业知识从理论上加以阐明。但是，当事物间的内在联系尚未被认识时，相关分析可根据它们的数量关系给理论研究提供线索。
2．相关和回归都是分析两变量间关系的统计方法 相关表示相互关系，回归表示依存关系。与相关分析一样，回归分析前也必须先作散点图，以判断两变量间的关系是否为线性趋势，有无离群点等。
3．积差和法相关与等级相关的应用范围是不同的 积差和法相关计算相关系数r适用于双变量正态资料；等级相关可用于难以判定其总体究竟属何种分布的资料，因而应用范围较广。一般来说，能用积差和法相关计算的资料不应用等级相关计算。因此，资料明显呈偏态分布或者原始资料只能用等级划分或难以判定资料属何种分布的，才宜按等级相关处理。
4．回归系数的统计学意义 不能仅根据回归系数假设检验之P值判断回归效果的优劣，因P值除与回归系数的大小有关外，还与样本含量有关。对于判断大样本回归系数的统计学意义尤其要谨慎。要想说明回归的贡献大小，需用决定系数r2作定量的度量。
5．回归方程的使用范围为自变量x原观察数据的范围，而不能随意外推，因为我们并不知道在这些观察值的范围之外，两变量间是否也存在同样的直线关系。
复习思考题
1．10名20岁男青年的身高与前臂长度如下：
（1）计算相关系数。
（2）如有相关，则用回归方程来描述其关系并绘制回归线。
2．某地中小学近视眼底改变资料如下表，试分析不同年级与视力不良程度的关系。
3．相关与回归的联系与区别是什么？
4．应用直线回归与相关分析应注意哪些问题？
5．举例说明如何用直线回归方程进行预测和控制？
6．某资料的x与y的相关系数r＝0．8，查r界值表，得P＞0．05，可否认为x与y有较密切的相关关系？
7．某人喜得贵子，庭前种一棵小树，每月测子高与树高，数月后积累了一批子高与树高的数据。用直线相关分析，其结论：子高与树高具有相关性。请加以评述。
8．求得r＝0．85，可认为________。
A．两变量一定相关 B．两变量关系非常密切
C．两变量关系不密切 D．两变量无任何关系
E．两变量的关系尚无法确定
9．在直线回归分析中，︱b︱值越大，________。
A．所绘散点越靠近回归线 B．所绘散点越远离回归线
C．回归线对x轴越平坦 D．回归线越陡
E．回归线在y轴上的截距越大
10．在分析相关系数时，应注意________。
A．根据r值可直接判断相关的密切程度
B．根据r值可直接判断相关的方向
C．若r＞0．5，即可认为两变量存在直线相关
D．r值经假设检验后才能确定有无直线关系
E．若︱r︱＞0．75即可认为存在高度相关关系
11．相关系数r的假设检验，其自由度为________。
A．n B．n－1 C．n－2
D．2n－1 E．2n
E．2n
12．
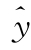＝7＋2x是1～7岁儿童以年龄（岁）估计体重（kg）的回归方程，若体重以市斤为单位，则此方程________。
A．截距改变 B．回归系数改变
C．截距和回归系数均改变 D．截距和回归系数均不改变
E．无法确定
13．相关系数和回归系数的关系是________。
A．︱r︱越大，︱b︱越大 B．︱r︱越大，︱b︱越小
C．r2＝b2 D．r2＝bxybyx
E．r与b之间毫无关系
14．根据样本资料算得相关系数r，经t检验，P＜0．01，则________。
A．两变量有高度相关
B．r来自有显著相关的总体
C．r来自总体相关系数不为0的总体
D．r来自总体相关系数大于0的总体
E．r来自总体相关系数小于0的总体
（孙 峰）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
