(一)农业农村信息化经济增长模型
C-D生产函数是Charles Cobb与Paul Dauglas在哈罗德—多马模型的资本产出比及资本储蓄率不变的假设基础上加以突破,用简单的形式对生产投入与产出的关系进行了分析。C-D生产函数的最初形式为:Y=AKαLβ。为测算农业信息化对农业经济增长的贡献,本文将根据罗默(Paul M.Romer)提出的新经济增长理论,对C-D生产函数进行修正。在当今的信息经济时代,信息要素已成为促进科技进步的最主要来源,因此可以用信息要素近似替代科技进步作为决定经济增长的第三因素,并将C-D生产函数修正为:
![]()
其中,Y代表我国农林牧渔业总产值;A代表剔除了农业信息化因素后的技术进步,由于本文讨论的时间跨度有限,因此设定为常数;K表示了农村全社会的固定资产投资总额,用于代表资本;L表示第一产业的就业人口,用于代表劳动力;I表示北京市农业农村信息化指数,用于代表信息化发展水平。
两边取对数:
![]()
令Y’=log(Y),A’=log(A),K’=log(K),L’=log(L),I=log(I),代入到公式(2)中,可得出新的线性回归模型:
![]()
(二)农业农村信息化指数模型回归
根据之前建立的道格拉斯生产函数模型,提取相应数据。为了保证数据的一致性,必须将影响2004年至2013年之间价格指数剔除。以2004年为基年,剔除因价格浮动可能造成影响的农林牧渔业总产值和农村全社会固定资产投资两项数据所带来的影响,最终将农业农村信息化发展水平总指数I、剔除价格因素的农林牧渔业总产值Y、剔除价格因素的农村全社会固定资产投资总额K、第一产业就业人口L分别取对数,得到公式3所需的数据,整理后如表3-5所示:
表3-5 取对数后北京市农业农村信息化贡献率测算的模型数据
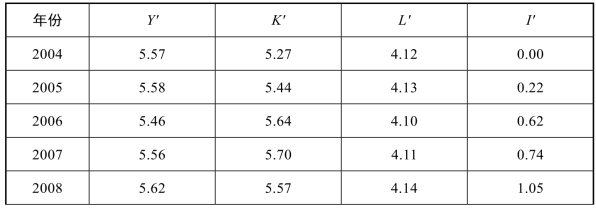
续表

运用SPSS19.0,采用Enter 法对表3-5中数据Y′Y′、K′K′、L′L′、I′I′进行线性回归分析,回归分析结果如表3-6。
表3-6 总指数模型回归结果
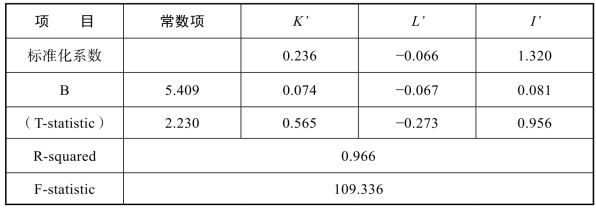
根据表3-6总指数模型回归的结果看,R2检验为0.966,表明所选样本与总体的拟合优度较好;F检验109.336,表明整个模型的线性程度很好;T检验的各项数值表明模型中各自变量对经济增长的解释度较高;并且,常数项、K、L和I分别以99%、90%、99%和99%的概率通过检验。回归结果表明,模型整体上能够通过检验,且对现实具有良好的模拟效果。据此,农业农村信息化总指数对农业经济增长的影响模型如下:
![]()
公式(4)又可变形转换为:
![]()
(三)信息化对农业经济增长的贡献
由前面的测算数据,我们得出了2004—2013年10年间北京农业信息化发展水平指数的增长情况,根据指数增长情况以及指数增长与农业经济增长之间的关系,可以测算出近10年农业农村信息化对农业经济增长的贡献率,如表3-7所示。
表3-7 北京农业农村信息化贡献率测算结果
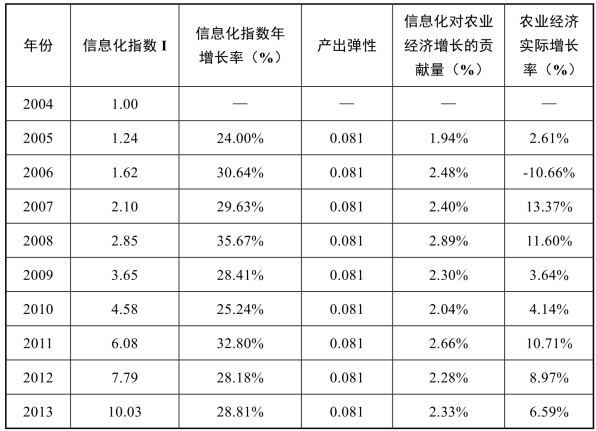
由图3-6可知,10年来北京市农业经济增速波动较大,从曲线本身来看没有形成稳定的变化趋势。由于2006年农业经济增长率为负值,农业经济产值回到了相对的低位,甚至低于2004年的产值,因而2006年成为10年间增长率曲线的极值波谷,从而较大地拉升了2007年的增长率,其后受国际金融危机造成经济整体低迷的影响,在2009年和2010年再次出现了农业经济增长率下滑的态势,近3年增长率变化较为稳定。尽管10年间农业经济增长率变化趋势波动明显,但是其中信息化的贡献一直较为平稳,基本维持在2%—3%之间,也即信息化能够对农业经济增长贡献2—3个百分点,表明加快农业农村信息化发展是促进农业经济增长的重要手段。
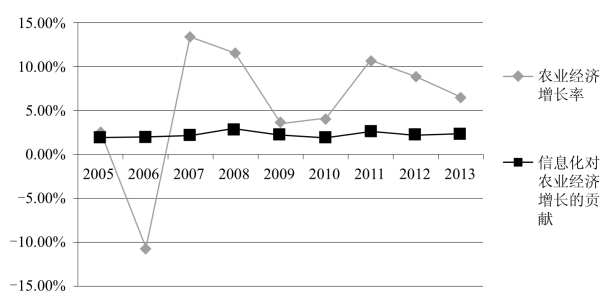
图3-6 2004—2013年北京市农业农村信息化贡献率的变化情况
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















