样本容量的确定

第四节　样本容量的确定

要考虑样本容量和结构问题。样本的容量究竟要多大才算是合适的?例如在民意测验中，要调查多少人才能反映全国几亿人口的意见?在粮食产量调查中，要调查多少亩才能反映全省几千万亩播种面积的亩产水平?等等。调查单位多了会增加组织抽样的负担，甚至造成不必要的浪费；若调查单位太少又不能够有效地反映情况，直接影响着推断的效果。样本的容量取决于对抽样推断准确性、可靠性的要求，而后者又因所研究问题的性质和抽样资料的用途而不同，很难给出一个绝对的标准。但在抽样设计时应该重视研究现象的差异、误差的要求和样本容量之间的关系，做出适当的选择。对相同的样本容量，还有容量的结构问题，例如一个区要求抽取500人进行调查，它可以是先抽5个社区，然后每社区抽100人，也可以是先抽10个社区，然后每社区抽50人等等，样本容量的结构不同，所产生的效果也不同。抽样设计应该善于评价而且有效利用由于调整样本结构而产生的效果。

一、必要抽样单位数的推算

组织抽样调查的一项重要工作是要确定合适的样本容量。在设计时候，通常是先根据研究问题的性质确定允许的误差范围Δ和必要的概率保证程度(或概率度t)，然后根据历史资料或其他试点资料确定总体的标准差σ，通过抽样平均误差公式来推算必要样本单位数n。

在重置抽样下(有放回，理论情况下)，样本平均数的误差公式:μ²=σ²/n；

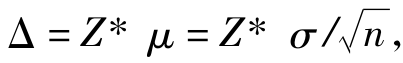，所以，必要的样本单位数:n=Z²*σ²/Δ²　　(6.27)

在不重置抽样下(无放回，一般情况下)，样本平均数的误差公式

所以，必要的样本单位数:n=N*Z²*σ²/(N*Δ²+Z²*σ²)　　(6.29)

从不重置平均数抽样误差公式中，可知在n/N比例很小，可以忽略不计的情况下，重置抽样的必要单位数n=Z²*σ²/Δ²也可以适用于不重置抽样的场合。

同样，重置抽样和不重置抽样的成数样本必要单位数分别为:

n=Z²*P(1－P)/Δ²　　　　　　　　　　　　　　(6.30)

n=N*Z²*P(1－P)/(N*Δ²+Z²*P(1－P))　　　　　　　　　　　(6.31)

从上式可以看出，必要的样本单位数受允许的误差范围Δ的制约，Δ要求愈小则样本单位数n就需要愈多，但两者并不保持反比例的变化。以重置抽样来说，在其他条件不变情况下，误差范围Δ缩小一半，则样本单位数n必须增至四倍，而Δ扩大一倍，则样本单位数只需原来的1/4。所以在抽样组织中对抽样误差可以允许范围要十分慎重的考虑。

二、注意事项

必要抽样单位数推算时注意事项大致如下:

(1)计算样本容量时，一般总体的方差与成数都是未知的，可用有关资料替代:用历史资料已有的方差与成数代替；或者是在进行正式抽样调查前进行几次试验性调查，用试验中方差的最大值代替总体方差；或者是成数方差在完全缺乏资料的情况下，就用成数方差的最大值0.25代替。

(2)如果进行一次抽样调查，同时估计总体均数与成数，用上面的公式同时计算出两个样本容量，可取一个最大的结果，同时满足两方面的需要。

(3)上面的公式计算结果如果带小数，这时样本容量不按四舍五入法则取整数，取比这个数大的最小整数代替。例如计算得到:n=58.08，那么，样本容量取59，而不是58。

三、范例

［例6.14］对某地区人们的生活质量进行调查，根据以往正常的经验数据，已知经济收入的标准差σ=500元，生活满意度p=70%。采用随机重复抽样方式，需要在95.45%的概率保证下，抽样平均收入的误差范围不超过2000元，抽样合格率误差范围不超过15%，试求必要的抽样单位数。

解:已知，1－α=95.45%，z=2，按抽样平均数与成数计算的样本容量分别是:

n1=Z²*σ²/Δ²=22*5002/0.152=44444445(人)，

n2=Z²*p(1－p)/Δ²=22*0.7*0.3/0.152=38(人)

取以上计算结果中较大者，即n=44444445.应抽取4444.45万人作样本以保证抽样调查的准确性。这就是社会抽样调查的困难。

应该说，以上我们讨论的是简单随机抽样，其他不同的抽样方法，如分层抽样、整群抽样等样本估计误差有所不同，若感兴趣，可以参阅抽样调查的相关书籍。

当总体分布未知或总体为非正态分布时，只要样本是大样本(一般认为n＞30为大样本)，根据中心极限定理，样本均值μ近似服从正态分布，并且用样本方差S²来估计总体方差σ²，因而也可以用z统计量来进行区间估计。